БІОМЕХАНІКА, БІОРЕОЛОГІЯ ТА ГЕМО­ДИНАМІКА

Біологічні тканини складні за своєю будовою, неод­норідні за своїм складом, їх структура і властивості визна­чаються тими функціями, які вони виконують в живих ор­ганізмах. В морфології виділяють декілька типів тканин -епітеліальну, тканини внутрішнього середовища (кров і лім­фу), сполучну, м'язову, нервову. Всі вони, як правило, ма­ють клітинну будову, складну структуру, і всім цим ткани­нам притаманний механічний рух у тій чи іншій мірі, почи­наючи з внутрішньоклітинних мікрорухів скорочувальних білкових ниток до макрорухів окремих органів та систем. Деякі з тканин призначені для виконання опорно-рухової функції і в процесі життєдіяльності підлягають значним механічним навантаженням. Різні форми механічного руху в живих системах вивчає біомеханіка, основи якої як науки про закони механічних рухів у біологічних системах запо­чатковані за часів Арістотеля, Леонардо да Вінчі, Бореллі, Галілея, Декарта, Гука, Ейлера, Бернуллі, Юнга, Гельм-гольця, Пуазейля та ін. (Зауважимо, що останні четверо бу­ли професорами медицини).

При вивченні деяких механічних властивостей біологічних тканин зручно уявляти їх у вигляді суцільних середовищ, не розглядаючи їх мікроструктуру і абстрагуючись від їх клітинної будови. Середовище може розглядати­ся як суцільне, якщо відстані, на яких змінюються його усе­реднені властивості (наприклад, густина, в'язкість тощо), значно перевищують розміри частинок (у нашому випадку -клітин, формених елементів), з яких складається середови­ще. У цьому випадку реальну тканину можна поділити на ряд елементарних об'ємів, розміри яких значно перевищу­ють розміри клітини, і до кожного з них застосовувати за­кони механіки з метою описання різних механічних явищ, таких як плин чи деформація середовища.

Розділ механіки, що вивчає плин і деформацію суціль­них середовищ, зветься реологією. Вивчення цих рухів у біологічних системах становить задачу біореології. Розгля­немо деякі важливі поняття реології.

Виділимо у суцільному середовищі елементарний об'єм ΔV з масою Am. Сили F, що діють у суцільному середовищі, можна віднести до одиниці маси (об'єму) чи одиниці площі поверхні.

Позначимо силу, що діє на одиницю маси речовини, через f = F/Δm; аналогічним способом визначається і ве­личина сили, що діє на одиницю об'ємуf=F/ΔV - так зва­на об'ємна сила. Наприклад, об'ємні сили інерції і тяжіння відповідно дорівнюють f= Δm -a/ΔV = ρ -a; f = Δm -g/ΔV= ρ*g.

З цих виразів випливає, що величини об'ємних сил не залежать від розмірів і мас тіл, а визначаються лише усе­редненими властивостями тіл (густиною ρ) і характеристи­ками їх механічного руху (прискоренням а). Вони діють одночасно на всі елементарні об'єми речовини, їх зручно використовувати для опису плину і деформації реальних су­цільних середовищ. Так, наприклад, використання цих сил дозволяє в зручній формі записати рівняння руху різних рідин, в тому числі і крові. (Слід підкреслити, що описуючи рух суцільних середовищ, використовують не лише об'ємні сили, а й об'ємну густину енергії w = ΔW/ΔV, яка характе­ризує величину енергії, що припадає на одиницю об'єму).

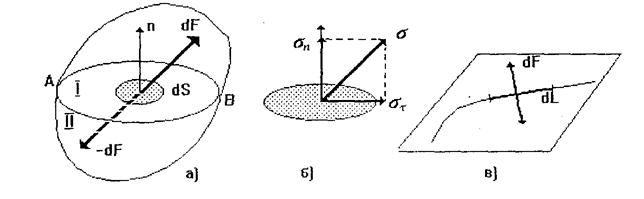
Різні ділянки середовища можуть взаємодіяти між со­бою по поверхнях розділу, в цьому випадку зручно кори­стуватися поверхневими силами, тобто силами, що діють на одиницю площі поверхні. Нехай дві ділянки тіла І і II ме­жують між собою поверхнею АВ (мал. 1.1).

Мал. 1.1. Сили, які діють на поверхні розділу середовищ.

Виділимо на поверхні АВ малу площу dS, на яку під деяким кутом до нормалі діє сила dF (мал. 1.1 а). У цьому випадку характеристикою поверхневих сил є величина на­пруження а, яка дорівнює силі, що діє на одиницю площі: а = dF/dS [Ж/и²]. Зручно ввести дві складові а по відношенню до вектора п нормалі до елемента поверхні dS: нормальну складову а_п, що діє перпендикулярно до площи­ни, і тангенціальну а_п спрямовану по дотичній до поверхні dS (мал. 1.16). Саме перша складова містить в собі скалярну величину - тиск Р, що дорівнює відношенню величини си­ли до величини площі поверхні: Р = F/S.

Іншим прикладом дії поверхневих сил є явище поверх­невого натягу, яке характеризується коефіцієнтом поверх­невого натягу а. Цей коефіцієнт чисельно дорівнює силі dF, яка діє на одиницю довжини довільного контура dL на поверхні і спрямована по дотичній до поверхні (мал 1.1 в):

а= =dF/dL[H/M].

Поверхневі сили використовують для опису явищ де­формації, плину в'язких середовищ, пластичності, повзу­чості, поверхневого натягу тощо, які спостерігаються при функціонуванні біологічних тканин.