Второе начало термодинамики. Энтропия

Первое начало термодинамики, являющееся, по существу, вы­ражением закона сохранения энергии, не указывает направления возможного протекания процессов. Так, например, по первому началу термодинамики, при теплообмене одинаково возможным был бы как самопроизвольный переход теплоты от тела более на­гретого к телу менее нагретому, так и, наоборот, от тела менее на­гретого к телу более нагретому. Из повседневного опыта, однако, хорошо известно, что второй процесс в природе нереален; так, на­пример, не может самопроизвольно нагреться вода в чайнике вследствие охлаждения воздуха в комнате. Другой пример: при падении камня на землю происходит его нагревание, эквивалент­ное изменению потенциальной энергии, обратный процесс — са­мопроизвольное поднятие камня только из-за его охлаждения — невозможен.

Второе начало термодинамики, так же как и первое, является обобщением данных опыта.

Существует несколько формулировок второго закона термоди­намики: теплота самопроизвольно не может переходить от тела с меньшей температурой к телу с большей температу­рой (формулировка Клаузиуса), или невозможен вечный двига­тель второго рода (формулировка Томсона), т. е. невозможен такой периодический процесс, единственным результатом которого было бы превращение теплоты в работу вслед­ствие

В тепловой машине совершается работа за счет переданной теплоты, но при этом часть теплоты обязательно передается холодильнику. На рис. 10.4 схематически показаны соответственно невозможный (а) и возможный (б), по второму началу, периодиче­ские процессы.

Рассмотрим некоторые термодинамические понятия, которые позволяют количественно выразить второе начало термодинамики.

Процесс 1 —2 называют обратимым, если можно совершить обратный процесс 2—1 через все промежуточные состояния так, чтобы после возвращения системы в исходное состояние в окру­жающих телах не произошло каких-либо изменений.

Обратимый процесс является физической абстракцией. Все ре­альные процессы необратимы хотя бы из-за наличия силы тре­ния, которая вызывает нагревание окружающих тел. Некоторые характерные примеры необратимых процессов: расширение газа в пустоту, диффузия, теплообмен и т. д. Для возвращения систе­мы в начальное состояние во всех этих случаях необходимо совер­шение работы внешними телами.

Циклом или круговым процессом на­зывают процесс, при котором система возвращается в исходное состояние.

График цикла представляет собой зам­кнутую линию. Цикл, изображенный на рис. 10.5, — прямой, он соответствует тепловой машине, т. е. устройству, кото­рое получает количество теплоты от неко­торого тела — теплоотдатчика (нагрева­теля), совершает работу и

отдает часть этой теплоты другому телу — теплоприемнику (холодильнику) (рис. 10.4, б).

В этом цикле рабочее вещество (газ) в целом совершает положи­тельную работу (рис. 10.5): в процессе 1—а—2 газ расширяется, ра­бота положительна и численно равна площади под кривой 1—а—2; в процессе 2—б—1 работа отрицательна (сжатие газа) и численно равна площади под соответствующей кривой. Алгебраическое сум­мирование дает в целом положительную работу, совершенную газом за цикл. Она численно равна площади, ограниченной замкнутой кривой 1—а—2—б—1.

Коэффициентом полезного действия тепловой машины или прямого цикла называют отношение совершенной рабо­ты к количеству теплоты, полученному рабочим веществом

от нагревателя:

Так как работа тепловой машины совершается за счет количе­ства теплоты, а внутренняя энергия рабочего вещества за цикл не изменяется (AU = 0), то из первого закона термодинамики следу­ет, что работа в круговых процессах равна алгебраической сумме количеств теплоты: A = Q_X + Q₂.

Следовательно,

Количество теплоты Q_v полученное рабочим веществом, положи­тельно, количество теплоты Q₂, отданное рабочим веществом хо­лодильнику, отрицательно.

Обратный цикл[2][2][2] соответствует работе холодильной машины, т. е. такой системе, которая отбирает теплоту от холодильника и передает большее количество теплоты нагревате­лю. Как следует из второго закона термодинамики, этот процесс (рис. 10.6) не может протекать сам собой, он происхо­дит за счет работы внешних тел. При этом газ совершает отрицательную ра­боту: работа сжатия в процессе 2—а—1 отрицательна, работа. В ре­зультате алгебраического расширения в процессе 1—6—2 положительна. В результате суммирова­ния получаем отрицательную работу га­за, численно равную площади, ограни­ченной кривой 2—а—1 —б—2.

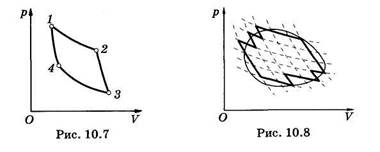
Рассмотрим цикл Карно (рис. 10.7), т. е. круговой процесс, со­стоящий из двух изотерм 1—2, 3—4, которым соответствуют тем­пературы Т₁ и Т₂ (Т₁ > Т₂), и двух адиабат 2—3, 4—1. В этом цик­ле рабочим веществом является идеальный газ. Передача количе­ства теплоты от нагревателя рабочему веществу происходит при температуре T₁ а от рабочего вещества к холодильнику — при температуре Т₂. Без доказательства укажем, что КПД обратимого цикла Карно зависит только от температур Т₁ и Т₂ нагревателя и холодильника:

Карно, исходя из второго начала термодинамики, доказал сле­дующие положения: КПД всех обратимых машин, работающих по циклу, состоящему из двух изотерм и двух адиабат, с нагрева­телем при температуре Т_г и холодильником при температуре Т₂, равны между собой и не зависят от рабочего вещества и конструк­ции машины, совершающей цикл; КПД необратимой машины меньше КПД обратимой машины.

Эти положения на основании (10.9) и (10.10) можно записать в виде

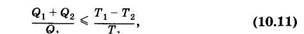
где знак «=» относится к обратимому циклу, а знак «<» — к необ­ратимому.

Это выражение представляет собой количественную формули­ровку второго начала. Покажем, что ее следствием являются обе качественные формулировки, приведенные в начале параграфа.

Допустим, что происходит теплообмен между двумя телами без совершения работы, т. е. Q_l + Q₂ = 0. Тогда [см. (10.11)] Т₁ - Т₂ > 0 и T₁ > T₂, что соответствует формулировке Клаузиуса: в самопро­извольном процессе теплота передается от тел с более высокой тем­пературой к телам с более низкой.

В том случае, если тепловая машина полностью затрачивает всю полученную при теплообмене энергию на совершение работы и не отдает энергию холодильнику, Q₂ = 0 и из (10.11) имеем

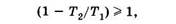
что невозможно, так как Т₁ и Т₂ положительны. Отсюда следует формулировка Томсона о невозможности вечного двигателя вто­рого рода. Преобразуем выражение (10.11):

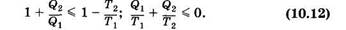
Отношение количества теплоты, полученного или отданного рабочим веществом, к температуре, при которой происходит теп­лообмен, называют приведенным количеством теплоты.

Поэтому (10.12) можно сформулировать так алгебраическая сумма приведенных количеств теплоты за цикл не больше нуля (в обратимых циклах равна нулю, в необратимых — меньше нуля).

Если состояние системы изменяется не по циклу Карно, а по некоторому произвольному циклу, то его можно представить в виде совокупности достаточно малых циклов Карно (рис. 10.8). Тогда выражение (10.12) преобразуется в сумму достаточно малых при­веденных количеств теплоты, что в пределе выразится интегралом

Выражение (10.13) справедливо для любого необратимого (знак «<») или обратимого (знак «=») цикла; dQ/T — элементарная при­веденная теплота. Кружок на знаке интеграла означает, что интег­рирование проводится по замкнутому контуру, т. е. по циклу. ¹ Рассмотрим обратимый цикл (см. рис. 10.5), состоящий из двух процессов аи б. Для него справедливо равенство:

На основе (10.13) для обратимых циклов имеем

Последнее означает, что сумма приведенных количеств тепло­ты цри обратимом переходе системы из одного состояния в другое не зависит от процесса, а для данной массы газа определяется только начальным и конечным состояниями системы. На рис. 10.9 показаны графики различных обратимых процессов (а, б, в), общими для которых являются начальное 1 и конечное 2 состоя­ния. Количество теплоты и работа в этих процессах различны, но сумма приведенных количеств теплоты оказывается одинаковой.

Физическую характеристику, не зависящую от процесса или перемещения, обычно выражают как разность двух значений не­которой функции, соответствующих конечному и начальному со­стояниям процесса или положениям системы. Так, например, не­зависимость работы силы тяжести от траектории позволяет выра­зить эту работу через разность потенциальных энергий в конечных точках траектории; независимость работы сил электро­статического поля от траекторий заряда позволяет связать эту ра­боту с разностью потенциалов точек поля, являющихся гранич­ными при его перемещении.

где S₂ и S₁ — энтропия соответственно в конечном 2 и начальном 1 состояниях. Итак, энтропия есть функция состояния систе­мы, разность значений которой для двух состояний равна сумме приведенных количеств теплоты при обратимом переходе систе­мы из одного состояния в другое.

Если процесс необратим, то равенство (10.15) не выполняется. Пусть дан цикл (рис. 10.10), состоящий из обратимого 2—б—1 и необратимого 1—а—2 процессов. Так как часть цикла необратима, то и весь цикл необратим, поэтому на основании (10.13) запишем

Согласно (10.15), тогда вместо (10.16) получим , или

Итак, в необратимом процессе сумма приведенных количеств теплоты меньше изменения энтропии. Объединяя правые части (10.15) и (10.17), получаем

где знак «=» относится к обратимым, а знак «>» — к необрати­мым процессам.

Соотношение (10.18) получено на основании (10.11) и поэтому также выражает второе начало термодинамики.

Установим физический смысл энтропии.

Формула (10.15) дает только разность энтропии, сама же энт­ропия определяется с точностью до произвольной постоянной:

Если система перешла из одного состояния в другое, то независи­мо от характера процесса — обратимый он или необратимый — изме­нение энтропии вычисляется по формуле (10.15) для любого обрати­мого процесса, происходящего между этими состояниями. Это обус­ловлено тем, что энтропия является функцией состояния системы.

Разность энтропии двух состояний легко вычисляется в обра­тимом изотермическом процессе:

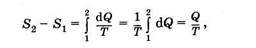
где Q — полное количество теплоты, полученное системой в про­цессе перехода из состояния 1 в состояние 2 при постоянной температуре Т. Последнюю формулу используют при вычислении изме­нения энтропии в таких процессах, как плавление, парообразова­ние и т. п. В этих случаях Q — теплота фазового превращения. Если процесс происходит в изолированной системе (dQ = 0), то [см. (10.18)] в обратимом процессе энтропия не изменяется: S₂ — S₁ = 0, S = const, а в необратимом — возрастает. Это можно проиллюстрировать на примере теплообмена между двумя тела­ми, образующими изолированную систему и имеющими темпера­туру Т₁ и Т₂ соответственно (Т₁ > Т₂). Если небольшое количество теплоты dQ переходит от первого тела ко второму, то при этом энтропия первого тела уменьшается на dS₁ = dQ/T₁, а второго — увеличивается на dS₂ = dQ/T₂. Так как количество теплоты неве­лико, то можно считать, что температуры первого и второго тел в процессе теплообмена не изменяются. Полное изменение энтро­пии системы положительно:

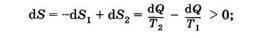
следовательно, энтропия изолированной системы возрастает. Ес­ли бы в этой системе происходил самопроизвольный переход теп­лоты от тела с меньшей температурой к телу с большей темпера­турой, то энтропия системы при этом уменьшилась бы:

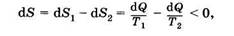
а это противоречит (10.18). Таким образом, в изолированной сис­теме не могут протекать такие процессы, которые приво­дят к уменьшению энтропии системы (еще одна формулиров­ка второго начала термодинамики).

Увеличение энтропии в изолированной системе не будет проис­ходить беспредельно. В рассмотренном выше примере температу­ры тел со временем выровняются, теплопередача между ними прекратится и наступит равновесное состояние (см. § 10.1). В этом состоянии параметры системы будут оставаться неизменными, а энтропия достигнет максимума.

Согласно молекулярно-кинетической теории, энтропию наибо­лее удачно можно охарактеризовать как меру неупорядоченности расположения частиц системы. Так, например, при уменьшении объема газа его молекулы вынуждены занимать все более опреде­ленные положения одна относительно другой, что соответствует большему порядку в системе, при этом энтропия убывает. Ког­да газ конденсируется или жидкость кристаллизуется при постоянной температуре, то выделяется теплота, энтропия убывает. И в этом случае происходит увеличение порядка в расположении частиц.

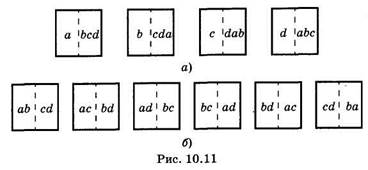
Неупорядоченность состояния системы количественно харак­теризуется термодинамической вероятностью W_тep. Для выясне­ния ее смысла рассмотрим систему, состоящую из четырех частиц газа: а, Ь, с, d (рис. 10.11). Эти частицы находятся в объеме, раз­деленном мысленно на две равные ячейки, и могут свободно в нем перемещаться.

Состояние системы, определяемое числом частиц в первой и второй ячейках, назовем макросостоянием; состояние системы, определяемое тем, какие конкретно частицы находятся в каждой из ячеек, — микросостоянием. Тогда (рис. 10.11, а) макросостоя­ние — одна частица в первой ячейке и три частицы во второй — осуществляется четырьмя микросостояниями. Макросостояние, соответствующее размещению четырех частиц равномерно по две в каждой ячейке, осуществляется шестью микросостояниями (рис. 10.11,6).

Термодинамической вероятностью называют число спосо­бов размещения частиц или число микросостояний, реали­зующих данное макросостояние.

В рассмотренных примерах W_тep = 4 в первом случае и W_тep = 6 во втором. Очевидно, что равномерному распределению частиц по ячейкам (по две) соответствует большая термодинамическая веро­ятность. С другой стороны, равномерное распределение частиц от­вечает равновесному состоянию с наибольшей энтропией. Из те­ории вероятностей ясно, что система, предоставленная самой се­бе, стремится прийти к макросостоянию, которое реализуется наибольшим количеством способов, наибольшим количеством микросостояний, т. е. к состоянию с наибольшей термодинамиче­ской вероятностью.

Заметим, что если газу предоставить возможность расширять­ся, его молекулы будут стремиться равномерно занять весь воз­можный объем, при этом процессе энтропия увеличивается. Об­ратный процесс — стремление молекул занять лишь часть объема, например половину комнаты, — не наблюдается, этому соответст­вовало бы состояние со значительно меньшей термодинамической вероятностью и меньшей энтропией.

где k — постоянная Больцмана.

Второе начало термодинамики — статистический закон, в отличие, например, от первого начала термодинамики или вто­рого закона Ньютона.

Утверждение второго начала о невозможности некоторых процес­сов, по существу, является утверждением о чрезвычайно малой веро­ятности их, практически — невероятности, т. е. невозможности.

В космических масштабах наблюдаются существенные откло­нения от второго начала термодинамики, а ко всей Вселенной, так же, как и к системам, состоящим из малого числа молекул, оно неприменимо.

В заключение еще раз отметим, что если первый закон термо­динамики содержит энергетический баланс процесса, то вто­рой закон показывает его возможное направление. Аналогич­но тому, как второй закон термодинамики существенно дополня­ет первый закон, так и энтропия дополняет понятие энергии.