МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ. ФИЗИЧЕСКИЙ МАЯТНИК
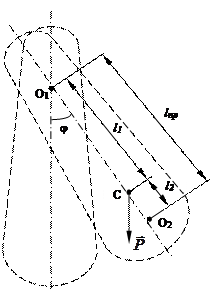 Рис. 6.1 Рис. 6.1
|
Всякое тело, подвешенное в точке, лежащей выше его центра тяжести, может колебаться и представляет собой физический маятник (рис. 6.1).
Если мятник отклонить от положения равновесия на угол j, то сила тяжести 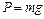 создает относительно оси вращения (проходит через т. О1 перпендикулярно к плоскости рисунка) вращающий момент
создает относительно оси вращения (проходит через т. О1 перпендикулярно к плоскости рисунка) вращающий момент
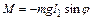 , (6.1)
, (6.1)
где l1 – расстояние от оси вращения до центра тяжести С, m – масса маятника, а угол j отсчитывается от вертикальной линии против часовой стрелки. Момент силы М стремится вернуть маятник в положение равновесия.
При малых углах отклонения колебания маятника будут близки к гармоническим. Действительно, при малых углах sinj » j и формула (6.1) принимает вид
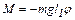 . (6.2)
. (6.2)
По основному закону динамики вращательного движения
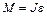 , (6.3)
, (6.3)
где J – момент инерции маятника относительно оси О1; 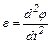 –угловое ускорение.
–угловое ускорение.
Подставляем M и ε в формулу (6.3):
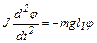 . (6.4)
. (6.4)
Обозначая 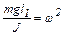 , перепишем равенство (6.4) в виде
, перепишем равенство (6.4) в виде
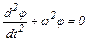 . (6.5)
. (6.5)
Уравнение (6.5) – дифференциальное уравнение гармонических колебаний. Решением этого уравнения является функция
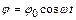 , (6.6)
, (6.6)
где j0 – максимальный угол отклонения маятника от положения равновесия, а 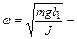 круговая (или циклическая) частота.
круговая (или циклическая) частота.
Для периода колебаний получаем
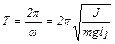 . (6.7)
. (6.7)
Величину 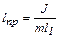 называют приведенной длиной физического маятника. Подставив это в выражение (6.7), найдем, что приведенная длина физического маятника равна длине математического маятника с таким же периодом колебаний.
называют приведенной длиной физического маятника. Подставив это в выражение (6.7), найдем, что приведенная длина физического маятника равна длине математического маятника с таким же периодом колебаний.
Точка, находящаяся на расстоянии lпр от точки подвеса по линии, проходящей через центр тяжести, называется центром качания.
Точка подвеса и центр качания обладают свойством обратимости: если центр качания сделать точкой подвеса, то прежняя точка подвеса станет новым центром качания, при этом период колебаний не изменится.
Для доказательства этого утверждения воспользуемся теоремой Штейнера: момент инерции тела относительно оси z равен моменту инерции этого тела относительно оси z’, проходящей через его центр инерции параллельно оси z, плюс произведение массы тела на квадрат расстояния между осями z и z’, т.е.
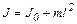 , (6.8)
, (6.8)
где J – момент инерции относительно оси z; J0 – момент инерции относительно оси z’; m – масса тела; l – расстояние между осями z и z’.
Рассмотрим вращение физического маятника вокруг точки О1 (см. рис. 6.1).
Проведем линию О1С и на ее продолжении возьмем точку О2, такую, что О1О2 = lпр1. Обозначим О2С = l2, так что 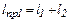 . Тогда
. Тогда
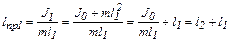 .
.
Таким образом, 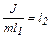 .
.
Теперь перевернем маятник и рассмотрим его вращение вокруг оси, проходящей через точку О2, при этом
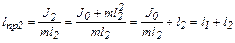 ,
,
откуда следует, что lпр1 =lпр2.
Дата добавления: 2015-06-17; просмотров: 2604;
