Сопротивление и мощность в символическом виде

Под комплексом полного сопротивления понимают частное от деления комплекса напряжения на комплекс тока:

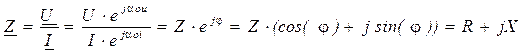
При записи комплекса полного сопротивления в показательной форме, модулем числа является полное сопротивление (Z), а аргументом угол (φ) – сдвиг по фазе, между напряжением и током. При записи в алгебраической форме, действительным числом является активное сопротивление (R), а мнимой частью – реактивное сопротивление (X).

Под комплексом полной мощности понимают произведение комплекса напряжения на сопряженный комплекс тока:

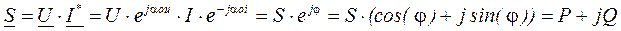
При записи комплекса полной мощности в показательной форме, модулем числа является полная мощность (S), а аргументом угол (φ) – сдвиг по фазе, между напряжением и током. При записи в алгебраической форме, действительным числом является активная мощность (P), а мнимой частью – реактивная мощность (Q).

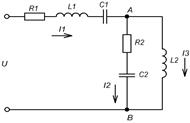
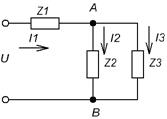
а) Заменяем данную схему эквивалентной:

б) Записываем условия задачи в символическом виде:

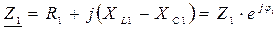
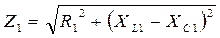
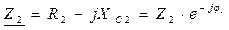
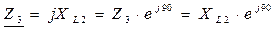
в) Рассчитываем эквивалентное сопротивление цепи:

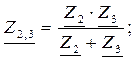
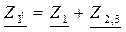
г) Рассчитываем токи в цепи:

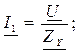
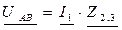
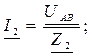
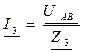
д) Рассчитываем мощности цепи:

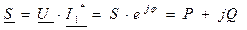
Пример:

Определить токи в ветвях цепи, активную реактивную и полную мощность, построить векторную диаграмму при следующих данных: R1=57,5 Ом, R2=40 Ом, С1=С2=106 мкФ, L1=95,5 мГн, U=400 В, f=50 Гц.

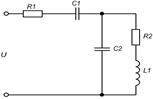
Решение (Символический метод):

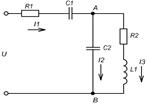
1. Заменяем данную схему на эквивалентную:

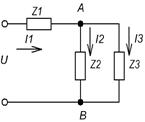
2. Записываем полные сопротивления ветвей цепи в символическом виде:

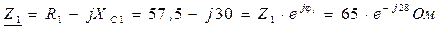
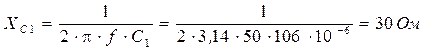
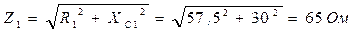
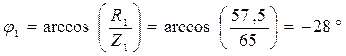
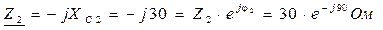
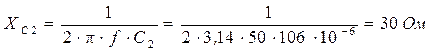
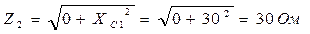
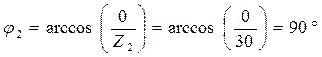
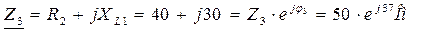
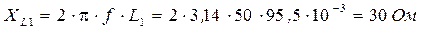
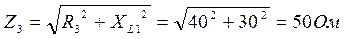
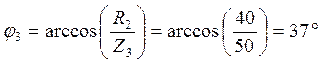
3. Определяем эквивалентное сопротивление цепи:

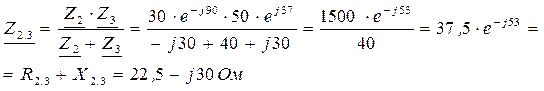
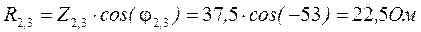
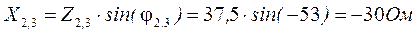
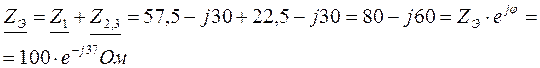
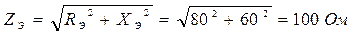
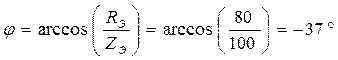
4. Определяем токи в ветвях цепи:

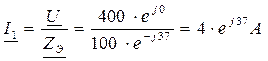
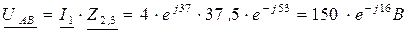
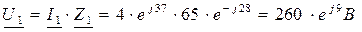
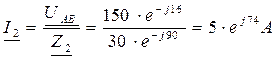
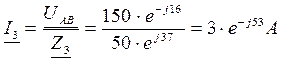
5. Определяем активную, реактивную и полную мощности цепи:

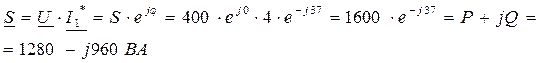
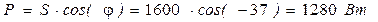
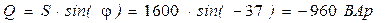
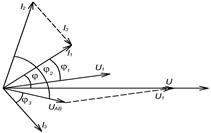
6. Строим векторную диаграмму: