Среднее квадратическое отклонение альтернативного признака
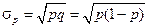 (5.29)
(5.29)
Если, например, 2% всех деталей бракованные (р = 0,02), то 98% — годные (q = 0,98), тогда дисперсия доли брака σp=0,02 · 0,98 = 0,0196. Среднее квадратическое отклонение доли брака составит:
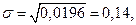 т.е. σ =14%
т.е. σ =14%
Для осуществления такого рода сравнений, а также сравнений колеблемости одного и того же признака в нескольких совокупностях с различным средним арифметическим используют относительный показатель вариации — коэффициент вариации.
Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:
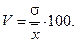 (5.30)
(5.30)
Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33 %.
Вариация признака обусловлена различными факторами, некоторые из этих факторов можно выделить, если статистическую совокупность разбить на группы по какому-либо признаку. В простейшем случае, когда совокупность расчленена на группы по одному фактору, изучение вариации достигается посредством исчисления и анализа трех видов дисперсий: общей, межгрупповой и внутригрупповой.
Общая дисперсия σ2 измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений признака х от общей средней 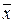 и может быть вычислена как простая дисперсия (по формуле (5.20) или взвешенная дисперсия по формуле (5.21).
и может быть вычислена как простая дисперсия (по формуле (5.20) или взвешенная дисперсия по формуле (5.21).
Межгрупповая дисперсия δ2 характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних 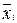 от общей средней
от общей средней 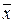 :
:
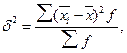 (5.31)
(5.31)
где f - численность единиц в группе.
Внутригрупповая (частная) дисперсия σ2i отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой группы xt (групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно:
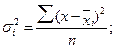 (5.32)
(5.32)
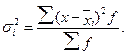 (5.33)
(5.33)
На основании внутригрупповой дисперсии по каждой группе, т.е. на основании σ2i можно определить общую среднюю из внутригрупповых дисперсий :
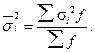 (5.34)
(5.34)
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:
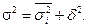 (5.35)
(5.35)
Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью — неизвестную, а также судить о силе влияния группировочного признака.
Очевидно, чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака (квалификационного разряда) на изучаемый признак (количество изготавливаемых изделий).
Поэтому в статистическом анализе широко используется эмпирический коэффициент детерминации (η2) — показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:
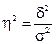 (5.36)
(5.36)
Эмпирический коэффициент детерминации показывает долю вариации результативного признака у под влиянием факторного признака х (остальная часть общей вариации у обуславливается вариацией прочих факторов). При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной связи — единице.
Эмпирическое корреляционное отношение — это корень квадратный из эмпирического коэффициента детерминации:
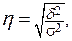 (5.37)
(5.37)
оно показывает тесноту связи между группировочным и результативным признаками.
Эмпирическое корреляционное отношение η, как и η2, может принимать значения от 0 до 1.
Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации.
Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна общей дисперсии (δ2 = σ2), т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака.
Для качественной оценки тесноты связи на основе показателя эмпирического корреляционного отношения можно воспользоваться соотношениями Чэддока :
| ηэ | 0,1-0,3 | 0,3-0,5 | 0,5-0,7 | 0,7-0,9 | 0,9-0,99 |
| Сила | Слабая | Умеренная | Заметная | Тесная | Весьма |
| связи | тесная |
Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.
Дата добавления: 2015-06-12; просмотров: 1397;
