Переключение диода из прямого направления в обратное.

Изучение импульсных частотных характеристик диодов

Цель работы - изучение переходных процессов в диоде, определение времени жизни неосновных носителей тока базы диода, сопротивление базы, контактной разности потенциалов.

Переходные процессы в диоде зависят от характера изменения режима диода. В связи с этим можно различать: процессы, связанные с переключением диода из прямого направления в обратное; процессы, связанные с переключением нейтрального (обратного) в прямом направлении (включение диода); процессы, связанные с переключением из прямого в нейтральное направление (выключение диода).

Переключение диода из прямого направления в обратное.

Пусть диод включен в схему, показанную на рис1. В зависимости от величины сопротивления R явления, протекающие в диоде, различны.

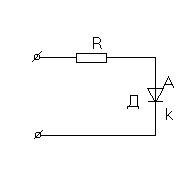
Рис.1. Последовательное включение диода и сопротивления.

Если сопротивление R мало, то при смене прямой полярности напряжения источника на обратную, ток в цепи определяется током диода, так как большая часть этого напряжения прикладывается к диоду. Если же сопротивление R велико, то ток через диод обусловлен этим сопротивлением, по крайней мере, до тех пор, пока конденсация неосновных носителей справа и слева от запорного слоя остается повышенной. Рассмотрим эти два случая.

Анализ переходных процессов в диоде основан на следующих предположениях:

1) Запорный слой имеет резкие границы;

2) Проводимость одной области много меньше проводимости другой;

3) Емкость запорного слоя не влияет на переходной процесс;

4) В полупроводнике сохраняется электронейтральность как во время переходных, так и во время стационарных процессов;

5) Уровень инжекции мал, т.е. концентрация неосновных носителей много меньше концентрации основных;

6) Время жизни носителей постоянно и не зависит от уровня инжекции;

7) Регенерация и рекомбинация в запорном слое отсутствуют;

8) Рассматривается плоская модель p-n перехода и краевые эффекты не учитываются;

9) Ширина базы диода W много больше диффузионной длины L.

Рассмотрим случай переключения диода из прямого направления в обратное, когда сопротивление R мало. Найдем ток в цепи (рис.1) при переключении напряжения Е с прямого на обратное. Если электропроводимость р - области больше электропроводимости n-области, ток через переход будет в основном дырочным. Чтобы найти величину этого тока, необходимо определить поведение концентрации дырок справа и слева от запорного слоя. Удобнее анализировать поведение концентрации дырок в n-области, поскольку они являются неосновными носителями. Ток дырок в n-области можно считать диффузионным, т.к. полагаем, что в полупроводнике сохраняется электрическая нейтральность, т.е. поле отсутствует. Тогда дырочный ток вблизи запорного слоя и будет полным током через переход, поскольку генерацией и рекомбинацией в запорном слое пренебрегаем. Поведение дырок в базе описывается уравнением диффузии

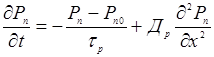(1)

здесь и далее полагаем 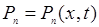, 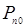- равновесная концентрация дырок 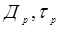- коэффициент диффузии и время жизни дырок. Распределение дырок в базе при протекании прямого тока (см. рис.2) через p-n переход имеет вид

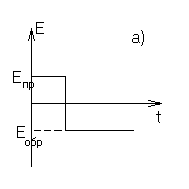
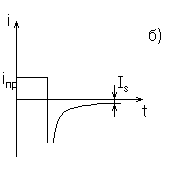
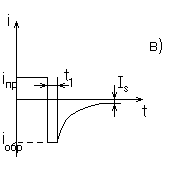
Рис.2. Временные диаграммы: а) импульс ЭДС; б) импульс тока диода при малом внешнем сопротивлении; в) импульс тока диода при большом внешнем сопротивлении.

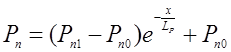(2)

где 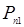- концентрация дырок у перехода при прямом смещении. Распределение дырок при обратном смещении, после окончания переходного процесса описывается уравнением

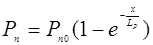(3)

В момент приложения обратного напряжения концентрация дырок в близи запорного слоя становится равной нулю:

P_n=0 при x=0; t>0 (4)

Уравнение (1) с учетом условий (2),(3) и (4) решается относительно концентрации дырок с помощью преобразования Лапласа. Если в конечном результате положить, что ток через переход

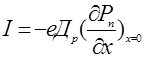(5)

и считать ток насыщения 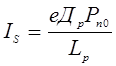пренебрежимо малым, то закон изменения обратного тока от времени будет иметь вид

(6)

где 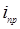- прямой ток диода;

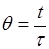- относительное время.

Разложение уравнения (6) в предельных случаях дают:

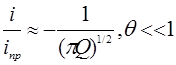(7)

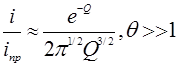(8)

______________________________________________________

*Здесь принято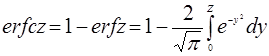

Из выражения (6) видно, что при 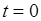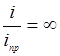. Реально величина выброса обратного тока ограничивается сопротивлением цепи и достигает конечного значения. Осциллограмма тока диода в случае малого сопротивления R дана на рис.2б.

Проанализируем качественно поведение концентрации дырок в базе диода. Как уже отмечалось, в момент подачи импульса обратного напряжения концентрация дырок на границе запорного слоя становится равной нулю. В глубине базы концентрация остается повышенной. Поэтому вблизи запорного слоя создается градиент концентрации дырок (рис.3), определяющий обратный ток через переход. С течением времени уменьшается концентрация дырок, уменьшается градиент концентрации, а поэтому и ток через диод. Уменьшение концентрации дырок в n-области связано с уходом их в p-область и рекомбинацией. Нетрудно понять, почему в идеализированном случае , когда сопротивление внешней цепи равно нулю, величина выброса обратного тока стремится к бесконечности, что следует из уравнения (6). Дело в том, что в момент подачи обратного напряжения концентрация дырок на самой границе запорного слоя мгновенно становится равной нулю. В любом другом сочетании базы в первое мгновение концентрация дырок остается неизменной, поэтому градиент концентрации дырок и дырочный ток через переход бесконечно велики. Реально электрическая цепь всегда имеет конечное активное сопротивление, которое ограничивает величины выброса обратного тока. Кроме того, длительность фронта обратного импульса напряжения также конечна. Поэтому концентрация дырок у запорного слоя приходит к нулю за конечное время. При этом распределение дырок в глубине базы успевает измениться и градиент концентрации дырок, а следовательно, и обратный ток диода будут ограничены.

Рассмотрим случай переключения диода из прямого включения в обратное, когда сопротивление R велико. При подаче импульса обратного напряжения в цепи, изображенной на рис.1, некоторое время некоторое время будет протекать неизменный по величине ток i_обр. Амплитуда и длительность плоской вершины обратного тока (рис.2В) определяются величиной Э.Д.С. Е_обр и сопротивлением R. В любом сечении базы дырочный ток:

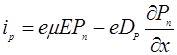(9)

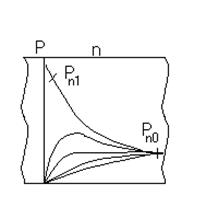
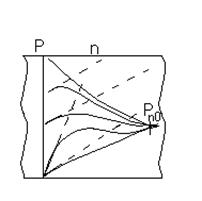
Рис 3 Рис.4.

Последовательное изменение Последовательное изменение

концентрации дырок в базе диода концентрации дырок в базе

при мгновенном изменении прямого диода при мгновенном

напряжения на обратное в случае изменении прямого

малого внешнего сопротивления напряжения на обратное

в случае большого внешнего

сопротивления.

При небольших уровнях инжекции дырочный ток можно считать диффузионным. Тогда ток через переход и концентрация дырок вблизи запорного слоя будут связаны уравнением

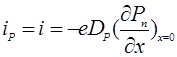(10)

Уравнение (10) позволяет сделать важный вывод. Поскольку ток через переход некоторое время остается постоянным (рис.2В). Градиент

концентрации дырок 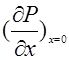также будет оставаться постоянным в течение времени формирования плоской вершины обратного тока. Спад тока будет сопровождаться уменьшением градиента концентрации дырок. Последовательное изменение концентрации дырок в базе показано на рис.4. Штрих-пунктирные прямые являются касательными к кривым распределения концентрации. Наклон касательных остается постоянным до тех пор, пока концентрация дырок не достигнет нулевого значения вблизи запорного слоя. Дальнейшее уменьшение концентрации дырок в глубине базы ведет к уменьшению градиента концентрации, а, следовательно, и тока через диод.

Найдем длительность плоской вершины обратного тока диода. Решение уравнения диффузии (1) с учетом условий (2), (3) и (10) описывает поведение концентрации дырок в базе на стадии формирования плоской вершины тока:

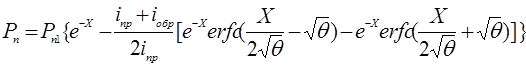(11)

где 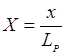- относительная координата.

При Х=0 уравнение (11) примет следующий вид:

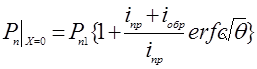(12)

В момент окончания формирования плоской вершины тока при

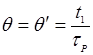
концентрация дырок вблизи запорного слоя 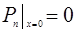. Тогда из уравнения (11) получим

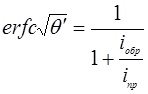(13)

График уравнения (13) приведен на рис.5.

Из графика можно заключить, что длительность плоской вершины

при 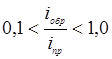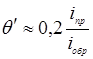(14)

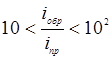при (15)

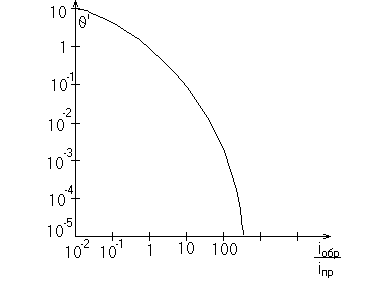
Рис.5. График уравнения (13), связывающий длительность плоской вершины обратного тока через диод.

Интервал времени, описываемый уравнением (15), мало интересен, т.к. он определяет длительность плоской вершины при больших обратных токах, когда эта длительность пренебрежимо мала. Поэтому наибольший интерес представляет уравнение (14), из которого длительность плоской вершины:

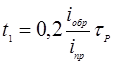(16)

После окончания плоской вершины формируется спад обратного тока, который описывается уравнением (6), если в нем за начало отсчета взято Q=Q .