Термокуполи
Термокуполи є еквівалентом граніто-гнейсових куполів відзначеного вище типу, що розвинені в межах рифейських та фанерозойських шовноскладчастих зонах.
Куполи даного типутакож являють собою концентрично-зональні тектонічні споруди, центральні частини (ядра) котрих, складено продуктами гранітизації та інтрузивними гранітоїдами, а оболонки – зонально динамометаморфізованими осадовими чи осадово-вулканогенними породами (рис. 4.9.6). При цьому динамометаморфічна зональність створюється метаморфізованими породами від амфіболітової до зеленосланцевої фації.
У межах шовноскладчастих зон термокуполи найчастіше концентруються на сіалічних ділянках (палеомікроконтинентах) і нерідко своєю появою забов'язані реоморфізму більш древніх граніто-купольних структур фундаменту. Припускається, що при їх формуванні, поряд із густинною інверсією, певну роль відігравали в'язкісна інверсія (видавлювання) та блоковий (тектонічне підняття) фактори, властиві для тектонічних зон відзначеного типу.
Граніто-гнейсові структури даного типу описано на байкалідах Кокчетавського мікроконтиненту (О.М.Розен та ін.), герцинідах Джунгарії (А.В.Смирнов) та Мугоджар (А.А.Абдулін та ін.)), мезозоїдах Забайкалля (В.В.Шевчук, Ю.В.Міллєр та ін.) та навіть альпідах Паміру (Ю.В.Міллер, М.С.Дюфур, та ін.).
Гібридні дислокаційні структури
Гібридними називаються дислокаційні структури, які утворилися при багаторазових накладеннях деформацій (рис. 4.10.1). До таких структур, наприклад, належать складки кліважних мікролітонів чи кристалізаційно-сланцюватих мікрошарків, або порушення в'язких розломів крихкими. У першому випадку гібридність обумовлена накладанням вигину на раніше сформовані кліваж чи кристалізаційну сланцюватість, а в другому – зміною пластичної деформації чи в'язкої течії – крихкою деформацією. Причому в другому випадку гібридизм супроводжується різкою зміною реологічного стану середовища: мезозонального (чи катазонального) – епізональним.
Формування гібридних структур відбувається у два і більше етапів (фаз) тектонічних деформацій (дислокаційних перетворень). При цьому на кожному наступному такому етапі (фазі) змінюється одна з наступних умов: 1) температура середовища, а в епізоні, крім того, ступені літифікації порід, 2) реологічні механізми деформацій, 3) напрямок дії та інтенсивність структуроутворюючих сил.
Між кожним відзначеним етапом (фазою) завжди має бути певна тектонічна пауза (перерва), під час якої деформації спадають до нуля.
4.10.1. Структурно-вікова шкала
Гібридні структури певною мірою зберігають елементи структурних парагенезисів кожного етапу (фази) тектонічних деформацій. Виділення таких парагенезисів та навіть їх окремих елементів і визначення співвідношень між цими елементами дозволяє тією чи іншою мірою впевненості визначати: 1) генетичні особливості дислокаційних структур кожного етапу (фази), 2) реологічні механізми, за допомогою яких вони формувалися, 3) термодинамічні умови, в яких реалізувалися деформації та 4) послідовність, в якій ці процеси відбувалися. Для документування такої послідовності в структурній геології використовуються структурно-вікові шкали та колонки з відповідною спеціальною індексацією.

Рис. 4.10.1. Поздовжнє накладання крихкого кліважу на кристалізаційну сланцюватість гнейсів та жилу аплітів (біле) аульської серії, яка перетинає
цю сланцюватість (Український щит). Р.Базавлук
Етапи (фази) деформацій (дислокаційних перетворень) позначаються літерами D, а їх послідовність – нижніми цифровими індексами на зразок D1,2,3....n.
Для позначення складок (або їх осьових поверхонь) вживається літера Fіз нижніми цифровими індексами, що відповідають етапам складкоутворення. Наприклад, F0 означає, що складка виникла на стадії седиментогенезу, а позначення F1.2...n – складки, що сформувалися на наступних етапах.
Розломи та фази їх підновлення позначаються літерою R з відповідним цифровими індексами.
Площинні структурні елементи позначаються літерою S і в тому числі: первинна шаруватість в осадових породах чи тіньова шаруватість у метаморфічних породах та первинна магматична смугастість – S0. При цьому кліваж та сланцюватість будь-яких типів, а також мігматитова чи будь-яка інша тектонічна смугастість з урахуванням послідовності формування – S1,2,3....n.
Таблиця 4.1. Зразок структурно-вікової шкали
| Етапи деформацій | Структурно-реологічні обстановки | Складки | Структурні та геометричні елементи | Вік деформацій | ||||
| площинні | лінійні | |||||||
| генетичні типи | індекси | типи | індекси | шар-ніри | ліній-ність | |||
| D0 | ПЕЗ | здимання | F0 | шаруватість | S0 | b0 | – | D1 |
| D1 | ВЕЗ | попере-чного вигину | F1 | механіч-на слан- цюва-тість | S1 | b1 | l1 | D2 |
| D2 | МЗ | кліваж-ної течії | F2 | кліваж | S2 | b2 | l2 | D3 |
| D3 | КЗ | слан-цюва-тої течії | F3 | кристалі-заційна сланцюва-тість | S3 | b3 | l3 | C1 |
| Dn | ВЕЗ | – | – | тріщину-ватість | Sn | – | – | Mz |
Для позначення лінійних геометричних і структурних елементів використовують малі літери: b– шарніри складок і l – лінійність. Причому, як і в попередніх випадках, додаються відповідні нижні цифрові індекси типу: b0– шарніри складок конседиментаційного етапу, b1або 2,3..n– шарніри складок наступних етапів.
Якщо в дислокаційних структурах якогось певного етапу існують різновиди відзначених елементів, то до відповідної літери додається штрих на зразок F2//.
Послідовність деформаційних процесів можна зафіксувати у вигляді структурно-вікової шкали наступного змісту (табл. 4.1).
Структурні ряди та циклічність
Явище гібридизму носить направлений, а в певних випадках і циклічний (ритмічний) характер. При цьому виникають структурні ряди прогресивні й регресивні.
Прогресивні структурні ряди. Ряди цього типу характеризуються поступовою зміною крихких деформацій пластичними (в'язкими). Вони відзначаються наступною послідовністю.
1. На рівні елементарних дислокаційних структур: 1) крихка тріщинуватість, 2) крихкий кліваж, 3) в'язкий кліваж, 4) кристалізаційна сланцюватість (чи гнейсуватість або будь-які інші структури в'язкої течії).
2. На рівні складних дислокаційних структур: 1) крихкий розлом, 2) крихко-в'язкий розлом, 3) субв'язкий розлом, 4) в'язкий кліважний розлом, 5) в'язкий кристалізаційно-сланцюватий чи гнейсуватий розлом.
Типовий приклад прогресивного ряду складок наведено вище в таблиці, що ілюструє поступальну зміну на певній ділянці геологічного середовища генетичних типів складчастих структур. Такий ряд починається з виникнення конседиментаційних складок. Подальше він нарощується складками вигину, котрі утворилися в структурно-реологічній обстановці, що відповідають первинній епізоні, та складками кліважної течії, які виникли в обстановці мезозони, і, нарешті, він закінчується складками кристалізаційно-сланцюватої течії, які сформувалися в обстановці катазони.
Утворення прогресивних структурних рядів завжди тісно сполучено з регіональним або локальним зростанням теплового потоку чи поступовим розігрівом середовища внаслідок магматичних ін'єкцій або метасоматичної й у тому числі гідротермальної діяльності, а також зі зростанням деформацій на кожному етапі. Ряди подібного типу характерні для ділянок формування термокуполів та "гарячих" в'язких протрузій. Вони, крім того, часто проявлені в осьових частинах великих фанерозойських зон зім'яття. В останніх вони до того ж обов'язково супроводжуються горизонтальною структурно-реологічною зональні-стю, тобто зміною по латералі дислокаційних утворень, які відповідають катазональним, – мезозональними, а останніх – епізональними.
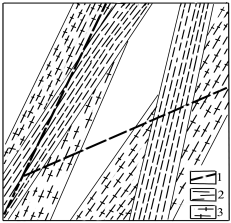
Рис. 4.10.2. Характерна для Українського щита регресивна послідовність формування розломів: 1 – крихкі та крихко-в'язкі, 2 – в'язкі кліважні, 3 – в'язкі кристалізаційно-сланцюваті та гнейсуваті
Регресивні структурні ряди. Ряди цього типу утворюють послідовність, у складі котрої в'язкі дислокаційні структури змінюються менш пластичними, а останні – крихкими (рис. 4.10.2, 4.10.3). Прикладом подібного ряду є наступна послідовність.
1. На рівні елементарних дислокаційних структур: 1) кристалізаційна сланцюватість, 2) в'язкий кліваж, 3) крихкий кліваж, 4) крихка тріщинуватість.
2. На рівні складних дислокаційних структур: 1) в'язкий кристалізаційно-сланцюватий розлом, 2) в'язкий кліважний розлом, 3) субв'язкий розлом, 4) крихко-в'язкий розлом, 5) крихкий розлом.
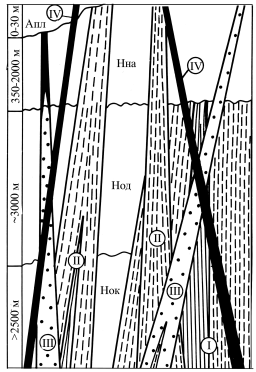
Рис. 4.10.3. Схема-колонка вікових взаємовідношень розломів різних реологічних типів (І – в'язкі кліважні, ІІ – субв'язкі, ІІІ – крихко-в'язкі, IV – крихкі) між собою та різновіковими формаційними комплексами субстрату (Алп – альпійський платформний, Нна – герцинський неоавтохтон континентальної стадії, Нод – герцинський островодужний, Нок – герцинський океанічний) у Західно-Мугоджарській шовній зоні. Хвилястими лініями позначено поверхні
міжформаційних незгідностей
Виникнення регресивних структурних рядів породжується зменшенням теплових потоків і відповідною зміною тектонічних режимів на кожному наступному етапі.
Крім відзначених, своєрідні регресивні структурні ряди виникають і в епізоні. Їх поява в цьому випадку зумовлена поступовим зростанням ступенів літифікації осадових порід, котра, як уже неодноразово відмічалося, прямо впливає на характер пластичності чи крихкості деформацій.
Ряди обох відзначених типів можуть бути повнимиі неповними. Перші складаються з дислокаційних структур епізони, мезозони та катазони в прогресивній чи регресивній послідовності, а другі відрізняються випаданням з їх складу дислокаційних структур однієї з названих стуруктурно-реологічної обстановки.
Повні структурні ряди характерні лише для древніх щитів, а у фанерозойських тектонічних областях вони розвинені на термокуполах та деяких ділянках великих шовноскладчастих зон. У той же час неповні структурні ряди найчастіше мають місце в більшості фанерозойських складчастих та платформних областей. Зокрема, у регресивних рядах каледонських та герцинських шовноскладчастих зон часто відсутні структури катазони, а в альпійських таких само зонах – і катазони, і мезозони. Наприклад, у складчастих спорудженнях Українських Карпат та Гірського Криму структурні ряди мають регресивний характер. Але представлені вони тільки епізональними складовими в наступній послідовності: 1) пошарові в'язкі механічно-сланцюваті розломи, 2) пошарові й січні крихко-в'язкі розломи, 3) січні крихкі розломи (Паталаха, Лукієнко, Гончар, 1996).
Циклічність (ритмічність) структурних рядів. Подібна циклічність знаходить свій вираз у поступовій (без суттєвої перерви в часі) зміні прогресивних структурних рядів регресивними. Одна така зміна приводить до створення одного циклу, а багаторазова – до циклічності. Остання характерна для шовноскладчастих зон і особливо тих, котрі відзначалися довготривалою тектонічною функціональністю. Часто такі цикли узгоджуються з метаморфічною циклічністю, утворюючи разом з нею тектоно-метаморфічну циклічність (Ю.В.Міллер, 1982 та ін.).
Використання стереограм для визначення просторових співвідношень дислокаційних структур та їх елементів
При вивченні гібридних дислокаційних структур та взагалі будь-яких дислокаційних накладень зручно користуватися стереографічними діаграмами, які надають можливість суміщати на горизонтальній проекції різні за орієнтуванням лінійні та площинні дислокаційні структури та їх окремі геометричні елементи. Наприклад, на такій проекції в системі географічних координат можна одночасно показати просторове положення окремих і навіть декількох систем тріщин, кліважу, сланцюватості, мігматитової смугастості, осьових поверхонь або шарнірів складок, лінійності, поверхонь деяких плоских тіл, контактів магматичних тіл, умовних поверхонь крихких та крихко-в'язких розломів, гідротермальних жил тощо. Для виконання подібної задачі у структурній геології використовують приблизно ті ж стереограми, які вживають при мікроструктурному аналізі. Зокрема, для побудови таких діаграм найчастіше використовують екваторіальну рівнокутову стереографічну сітку Ламберта – Шмідта, коротку характеристику котрої наведено в розд. "Мікроструктурний аналіз".
Техніка побудови діаграм подібного типу докладно описана в роботах І.О.Очеретенка та В.В.Трощенка "Стереографічні проекції у структурній геології" (М., 1978) та О.І.Родигіна "Структурные диаграммы" (Томск, 1980) та інших авторів. Тому в даній роботі ця техніка наведена в короткому викладі, запозиченому з робіт відзначених вище авторів.
4.10.3.1. Побудова стереографічної проекції прямої
Техніку побудови такої проекції найкраще розглянути на конкретному прикладі.
Наприклад, треба побудувати стереографічну проекцію прямої, яка відповідає якомусь лінійному структурному елементу типу шарніра складки, що має азимут падіння 298° і кут падіння 48°
Для виконання цієї задачі на екваторіальну сітку накладаємо кальку таким чином, щоб їх центри і відмітки N (північ) – 0° збіглися (рис. 4.10.4). Далі відраховуємо по азимутальній (зовнішній) шкалі сітки в напрямку руху годинникової стрілки 298° і помічаємо цей напрямок точкою a0. Для того щоб знайти стереографічну проекцію прямої, тобто точку перетину прямої з поверхнею верхньої півсфери, обертанням кальки навколо центра сумістимо відзначену точку з будь-яким кінцем горизонтального діаметра сітки, а потім на його протилежній частині розрахуємо по градусних поділках кут 48° у напрямку від лінії кола до центра сітки. Знайдена таким чином точка a є шуканою стереографічної прямої.
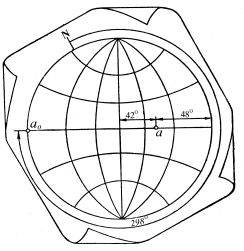
Рис. 4.10.4. Побудова проекції прямої по її азимуту і за кутом нахилу
Таким самим способом вирішується і зворотна задача. Зокрема, нехай стереографічною проекцією прямої є точка a (див. рис. 4.10.4). Сумістивши центри і позначки N (нулі на зовнішньому колі) кальки і сітки, проведемо через точку a і центр сітки пряму до перетинання з колом і по зовнішній шкалі сітки і визначимо значення азимута нахилу прямої (кут між північним напрямком центрального меридіана сітки і напрямком нахилу прямої a0, який замірювався за ходом годинникової стрілки). Потім поворотом кальки навколо центра потрібно сумістити позначку азимута нахиленої прямої (точку a0.) з горизонтальним діаметром сітки і по градусних розподілах визначити кількість градусів між проекцією прямої (точкою a) і колом сітки, тобто кут нахилу прямої до обрію (48°).
Побудова стереографічної проекції площини та її полюса
Просторове положення будь-якої площини, поміщеної в центр сфери, однозначно визначається за положенням її стереографічної проекції – дуги великого кола – і проекцією перпендикуляра, поставленого до неї в центрі сфери. Проекція перпендикуляра іменується полюсом площини. Такий засіб стереографічного проектування площин має цілий ряд переваг порівняно з побудовами їхніх дугових проекцій.
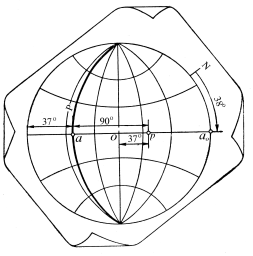
Рис. 4.10.5. Побудова проекції площини по азимуту і куту нахилу
Побудова стереографічної проекції площини.Як приклад розглянемо винесення на стереографічну сітку площини, що відповідає поверхні кліважу з азимутом ліній падіння 38° і кутом падіння 37°. Для цього від напрямку N меридіана відраховуємо по зовнішній шкалі сітки 38° і помічаємо цей напрямок на колі кальки точкою aо (рис. 4.10.5). Повернемо кальку навколо центра до суміщення точки ао з одним із кінців горизонтального діаметра сітки і, переконавшись у тому, що центри кальки і сітки збігаються, знайдемо проекцію лінії падіння площини, точку a. Для цього потрібно відрахувати на протилежній половині горизонтального діаметра значення кута лінії падіння 37° в напрямку від кола до центра сітки. Оскільки відлік падає в даному випадку між двох дуг (сітка градуюється, звичайно, через 2°), положення проекції визначається на око, шляхом інтерполяції, що варто мати на увазі при розв'язанні всіх наступних задач.
Відомо, що всі площини, які проходять через центр сфери, перетинають її по дугах великих кіл. Останні зображено на стереографічній сітці у виді меридіанів. Тому стереографічною проекцією нашої площини є дуга Р, проведена через точку a між двома сусідніми меридіанами з парними градусними поділками.
Для розв'язання зворотної задачі виконуються наступні операції.
Нехай стереографічною проекцією площини є дуга Р. Для рішення задачі, поєднавши цю дугу з відповідним меридіаном сітки і слідкуючи за тим, щоб центри кальки і сітки не розійшлися, відрахуємо на горизонтальному діаметрі сітки кількість градусів між колом і дугою Р (див. hbc). Не зрушуючи кальки, відзначимо точною a0 на окружності сітки напрямок лінії падіння площини (лінії a0).
Після цього, поєднавши поворотом кальки позначки N, визначимо по зовнішній шкалі сітки азимут падіння площини. Нагадаємо, що він завжди вимірюється по ходу годинної стрілки.
Які приклад пропонується побудувати полюс площини з азимутом падіння 38° і кутом падіння 37°.
Побудова полюса площини.Якщо прийняти дані по азимуту та куту падіння, що були використані в попередньому прикладі, то необхідно по зовнішній шкалі сітки відрахувати азимут падіння площини 38° і відзначити точкою a0 цей напрямок на кальці (позначки N кальки і сітки мають при цьому збігатися). Потім поворотом кальки навколо центра потрібно сполучити точку a0 з будь-яким кінцем горизонтального діаметра і від центра сітки в напрямку оцінки азимута падіння (точки a0 ) відрахувати значення кута падіння площини 37° (див. рис. 4.10.5). Точка p є полюсом нашої площини. Потрібно пам'ятати, що полюс завжди розташовується на продовженні лінії падіння площини, а його кутова відстань від проекції дуги даної площини, що вимірюється на горизонтальному діаметрі сітки, дорівнює 90°. Тому, у разі потреби побудови проекції дуги площини Р по її полюсу р достатньо відрахувати на горизонтальному діаметрі від точки р через центр сітки 90° і провести через отриману точку a відповідну дугу великого кола.
Коли потрібно знайти полюс р за заданою проекцією дуги площини Р, необхідно сполучити цю дугу з відповідним меридіаном сітки і, відрахувавши 90° по горизонтальному діаметру, відзначити на кальці шукану точку р.
Визначення азимута і кута падіння площини.Нехай точка р є полюсом площини Р. Поворотом кальки навколо центра сітки о помістимо точку р на екватор. Відрахувавши кількість градусних поділок між точкою р і центром сітки, одержимо значення кута падіння площини (див. рис. 4.10.5). Не зрушуючи кальки, відзначимо на ній положення найближчого від точки р кінця екватора точкою a0. Потім, повернувши кальку до суміщення її північної позначки N із нулем зовнішньої шкали сітки, відрахуємо азимут падіння площини – кут між північним кінцем центрального меридіана і точною a0.
Дата добавления: 2015-04-07; просмотров: 1030;
