Під кутом до діючої сили
Величина нормальних та дотичних напружень залежить від орієнтації площадок, в яких вони діють, відносно напрямку вектора сили Р.Зокрема, ці напруження зменшуються або збільшуються при зміні кута між відзначеними площадкою та вектором сили. У зв'язку з цим завжди існують окремі кутові положення площадок відносно вектора сили, в яких нормальне чи дотичне напруження дорівнює нулю, або навпаки, досягає певного максимального значення. Подібні відносно максимальні напруження називаються головним нормальними(smax)та головним дотичними (tmax).
Площадки, в яких діють головні нормальні та головні дотичні напруження, не збігаються. При цьому встановлено, що, площадки, в яких діютьголовні нормальні напруження, при одновісному розтяганні чи стисненні орієнтуються перпендикулярно до напрямку дії цих сил, а площадки, в яких діють головні дотичні напруження, – під кутом 45° до цих напрямків, і, крім того, величина головних дотичних напружень дорівнює половині головних нормальних (tmax=smax/2).
Просторові й кількісні співвідношення відзначених вище напружень визначаються графічно та на основі нескладних розрахунків, наведених нижче на прикладі одновісного розтягання стрижня (рис. 1.2.2).
Якщо зовнішня сила, що розтягає брусок, має значення Р, то повне напруження (р) у перетині, що має площу S, перпендикулярному до цієї сили, буде дорівнювати: p=Р/S.
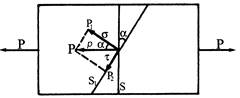
Рис. 1.2.2. Схема нормальних і дотичних напружень на довільно орієнтованій площадці S1 при одновісному розтяганні стрижня
У будь-якому іншому, орієнтованому під кутом a до площадки S, перетині площею S1, нормальне й дотичне напруження будуть дорівнювати:
s=Р1/S1 та t= P2/S1.
Якщо врахувати що: P1=P×cosa, Р2=P×sina, a S1=S/cosa, то за допомогою підставлень і спрощень рівнянь визначаємо, що
s=cosa×cosa Р/S =p cos2a,
t =sina×cosa Р/S = р×sina×cosa =1/2 p×sin2a.
Шляхом підбору значень кутів установлюється, що найбільше нормальне напруження при одновісному розтяганні діє в перетині, розташованому перпендикулярно до напрямку вектора сили, тому що cos2a=1, колиa=0. У свою чергу, найбільше дотичне напруження, яке складає половину найбільшого (у даному випадку повного) нормального, діє в перетинах, розташованих під кутом 45° до цієї сили, тому що при цьому куті sin2a= sin90° (тобто 2´45°) =1.
Нормальні напруження залежно від характеру зміни форми тіла поділяють на напруження розтягу та стиснення.
| |
Двовісна деформація зумовлюється дією двох пар взаємно перпендикулярних найбільших нормальних та дотичних напружень (рис. 1.2.3), а тривісна – трьома подібними парами в трьох взаємно перпендикулярних площадках (рис. 1.2.4).
При двовісній деформації tmax=(s1–s2)/2. При s1=s2 tmax=0.
В об'ємному напруженому середовищі існують максимальні, середні та мінімальні головні напруження: s1>s2>s3.
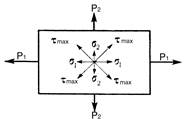
Рис. 1.2.3. Схема розташування максимальних нормальних та дотичних напружень при двовісній деформації
Середні напруження в певній точці виражаються як
sсер=(s1+s2+s3) /3
Якщо s1=s2=s3, то дотичні напруження, як і при двовісній деформації, відсутні. Це випадок урівноваженого всебічного стиснення чи розтягу (рис. 1.2.5). Подібне стиснення в геологічних середовищах, за аналогією з гідростатичним, називається літостатичним.
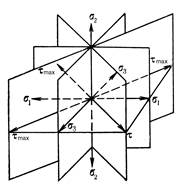
Рис. 1.2.4. Схема розташування максимальних нормальних та дотичних напружень при об'ємному напруженому стані
В інших випадках, коли максимальні нормальні напруження не рівні між собою (s1¹s2¹s3), відбувається деформація (стрес) середовища. При подібній нерівності дотичні напруження також не дорівнюють нулю. Максимальні дотичні напруження в цьому випадку проявляються на двох сполучених площадках, котрі ділять наполовину кут між найбільшою та найменшою осями нормальних напружень і дорівнюють tmax=(s1 -s3)/2 (див. рис. І.2.4).
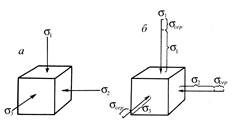
Рис. 1.2.5. Умови напружень літостатичні (а) та нелітостатичні (б)
Дата добавления: 2015-04-07; просмотров: 791;
