ЗЕМЛЯ И КОСМОС
1.1. Галактика и космические поля
1.1.1. Галактика
В настоящее время астрономы устанавливают миллионы звездных скоплений типа нашей Галактики, определенным образом расположенных во Вселенной. Мир галактик оказался удивительно разнообразен по форме и размерам. Так, Э. Хаббл делит их на 3 типа: эллиптические, спиральные и неправильные. Абсолютное большинство (80 %) среди нескольких тысяч ярчайших галактик относится к типу спиральных. К этому же типу относится и наша Галактика (Млечный Путь), имеющая размеры: диаметр – 100 000 световых лет (30 кпк или 1018 км), толщина – около 10 000 световых лет.
Парсек (пк, pc) распространённая в астрономии внесистемная единица измерения расстояний.
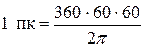 а.е. ≈ 206 264,8 а.е. = 30,8568∙1012 км = 3,2616 световых лет
а.е. ≈ 206 264,8 а.е. = 30,8568∙1012 км = 3,2616 световых лет
Астрономическая единица (а.е., au) – исторически сложившаяся единица измерения расстояний в астрономии, приблизительно равная среднему расстоянию от Земли до Солнца.
1 а. е.= 149 597 870 700 м
Световой год (св. г., ly) – внесистемная единица длины, равная расстоянию, проходимому светом за один год.
Из расчетов следует, что общее число звезд в нашей Галактике достигает 100 млрд., одной из которых является Солнце. Установлено, что в районе Солнца каждая вторая звезда является двойной. Имеются системы из трех, четырех и более звезд. В Галактике обнаружены и более сложные звездные системы – рассеянные и шаровые скопления, состоящие из совокупности звезд от нескольких десятков до нескольких тысяч. Около 100 миллиардов звезд Галактики составляют 98 % ее массы. Остальные 2 % вещества находятся в распыленном состоянии в виде газа и межзвездной пыли. Большая часть этого вещества скапливается в огромные облака – галактические туманности. В основном эти облака сосредоточены вблизи галактической плоскости.
На рис. 1.1, а схематически изображено распределение звездных объектов в пределах Галактики «с ребра». Кружочки соответствуют шаровым скоплениям. Положение Солнца отмечено крестиком (см. рис. 1.1, б). В системе Галактики условно выделяют ядро и пять разновозрастных подсистем (см. рис. 1.1, а). Почти 95 % массы Галактики сосредоточено вблизи галактической плоскости. При удалении от нее число звезд в единице объема резко убывает. На долю сферической составляющей, образующей корону Галактики, приходится всего около 5 % массы вещества. Линейные размеры ядра Галактики порядка 4 000 световых лет. Ядро Галактики является источником мощного радиоизлучения. Из центра Галактики исходит также гамма-излучение с энергией квантов порядка 0,5 МэВ.
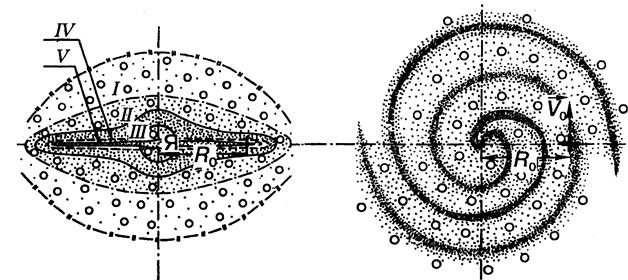
а б
Рис. 1.1 – Схема распределения звезд и шаровых скоплений Галактики в двух проекциях. Подсистемы Галактики: I – сферическая (гало); II – промежуточная сферическая; III – диск; IV – старая плоская; V – молодая плоская; Я – ядро.
В плоскости Галактики распределение звездных скоплений имеет достаточно ярко выраженный спиральный характер (см. рис. 1.1, б): от центральной области диска к периферии отходят спиральные ветви, в которых преимущественно сконцентрированы наиболее яркие звезды Галактики. Спиральные ветви Галактики – это волны плотности, распространяющиеся по галактическому диску.
Многие пространственные масштабы Галактики, а вместе с ними ее крупномасштабные характеристики зависят от принимаемого расстояния от Солнца до ее центра 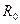 . Часто используют рекомендованное Международным астрономическим союзом значение
. Часто используют рекомендованное Международным астрономическим союзом значение 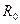 = 10 кпк. Обзор многочисленных определений
= 10 кпк. Обзор многочисленных определений 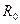 различными методами свидетельствует, что большинство из них дают оценки
различными методами свидетельствует, что большинство из них дают оценки 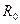 близкие к 8,5 кпк. Динамические характеристики Галактики зависят от принимаемой круговой скорости ее вращения
близкие к 8,5 кпк. Динамические характеристики Галактики зависят от принимаемой круговой скорости ее вращения 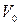 на расстоянии
на расстоянии 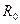 , и имеют величину порядка 25 км/(с*кпк).
, и имеют величину порядка 25 км/(с*кпк).
Галактика вращается дифференциально. Угловая скорость убывает от центра к периферии. Поэтому всякое заметное в масштабе Галактики структурное образование должно деформироваться и в конечном итоге «размываться» в течение 2-3 галактических лет.
По современным представлениям, спиральные волны плотности могут вращаться с постоянной угловой скоростью так, что их форма не деформируется вследствие дифференциального вращения диска. Угловую скорость вращения спирального узора исследователи оценивают по-разному. Наиболее вероятным представляется ее значение порядка 24 км/(с*кпк).
1.1.2. Солнечная орбита.
Наряду с движением Солнца вокруг центральных масс Галактики по орбите, близкой к эллиптической, плоскость этой орбиты вращается вокруг центра Галактики в направлении, обратном направлению движения Солнца. Это обратное смещение за время между двумя последовательными прохождениями Солнца через перигалактий (наименьшее расстояние от центра Галактики до Солнца, или апогалактий – наибольшее расстояние между ними), так называемый аномалистический период галактического движения Солнца, достигает 61°. Аномалистический период равен 176*106 лет. Момент последнего прохождения Солнца через апогалактий был 76*106 лет тому назад. Расстояние от центра Галактики в перигалактии 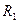 = 7,12 кпк, а в апогалактии
= 7,12 кпк, а в апогалактии 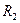 = 8,59 кпк; среднее расстояние
= 8,59 кпк; среднее расстояние 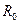 = 7,86 кпк, расстояние в настоящее время – 7,2 кпк. Линейная скорость в перигалактии 250 км/с, в апогалактии – 207 км/с. Правильные периодические изменения скорости галактического движения Солнца должны отражаться на движении планет и, в частности, на движении Земли и Луны.
= 7,86 кпк, расстояние в настоящее время – 7,2 кпк. Линейная скорость в перигалактии 250 км/с, в апогалактии – 207 км/с. Правильные периодические изменения скорости галактического движения Солнца должны отражаться на движении планет и, в частности, на движении Земли и Луны.
Длительность галактического года принимают в пределах круглых чисел (200 ± 20)* 106 лет.
1.1.3. Магнитные поля Галактики.
Магнитные поля (и их неизменный спутник – быстрые частицы) обнаруживаются во Вселенной везде, где только есть возможность их обнаружить.
В результате изучения поляризации света звезд установлено, что в Галактике имеется магнитное поле, силовые линии которого параллельны плоскости Млечного Пути и направлены вдоль ее спиральных ветвей. Индукция магнитного поля в межзвездном пространстве неодинаковая. Она характеризуется средним значением порядка 1 нТл. Верхний предел индукции магнитного ноля в районах созвездий Кассиопеи, Тельца и Стрельца 1….4 нТл, в Крабовидной туманности – 50 нТл.
В астрофизических условиях магнитное поле подобно «организму», питающемуся энергией, которую он черпает из звезд и галактик. Это небольшое количество энергии под влиянием слабого начального пола расходуется на возбуждение нового магнитного поля и именно этот малый расход вызывает непрекращающуюся активность в солнечной системе, Галактике, Вселенной. Магнитные поля создаются благодаря движениям непрерывной среды. Они неизменно порождают сложные проявления активности, которые иначе не могли бы возникать. Как только на возбуждение поля затрачена энергия, появляются почти безграничные возможности для дальнейшего развития активных процессов. Солнечные пятна, вспышки, протуберанцы – вот некоторые проявления активности на Солнце. Квазипериодические колебания солнечной активности с характерными периодами в 11 и 22 года – явление магнитного происхождения. Хотя солнечные магнитные поля вызывают эффекты, качественно влияющие на околосолнечное пространство и Землю, на их возбуждение расходуется 10-4 полной мощности Солнца.
Солнце – звезда среднего возраста, ничем не выделяется среди других звезд Галактики. Магнитное поле Солнца характеризуется индукцией порядка (1÷2)*10-4 Тл. В настоящее время открыто более 200 магнитных звезд, обладающих полями (1÷340)*10-2 Тл. Существуют плотные вырожденные звезды, обладающие мощными магнитными полями. Например, на «белых карликах» обнаружены магнитные поля индукцией 102 -103 Тл. Пульсары обладают магнитными полями, индукция которых достигает 108 Тл.
1.2. Солнце и Солнечная система
1.2.1. Солнце
Солнце – одна из звезд Галактики, вокруг которой вращаются девять планет, включая Землю. Среднее расстояние от Земли до Солнца, составляющее 149,6*106 км или одна астрономическая единица (а.е.). Радиус Солнца составляет 696 000 км или 109 радиусов Земли, масса – 1,99*1030 кг или
332*103 масс Земли, средняя плотность – 1 410 кг/м3 или 0,256 средней плотности Земли. Сила гравитации на поверхности Солнца в 28 раз больше силы гравитации на поверхности Земли.
Солнце – это огромный раскаленный газовый шар, вращающийся в том же направлении, что и Земля. Вращение Солнца неравномерно – на экваторе значительно быстрее, чем у полюсов. Период вращения Солнца у экватора составляет около 25 сут, у полюсов – 33 сут. Одной из особенностей Солнца является наличие на его поверхности пятен. Солнечные пятна представляют собой выход мощных «жгутов» – трубок магнитных силовых линий. Напряженность магнитного поля в крупных пятнах достигает 240 кА/м. Большинство крупных солнечных пятен биполярны. В образовании и размещении пятен на Солнце наблюдается 11-летний цикл, по истечении которого полярность пятен в разных полушариях меняется на обратную. Полный цикл пятнообразования на Солнце составляет 22 года.
Наряду с магнитным полем солнечных пятен, Солнце, по-видимому, имеет и дипольную компоненту, обусловленную её общим вращением. Однако индукция его невелика и вряд ли превышает несколько единиц 10-4 Тл в районе полюсов. Наблюдаемое излучение Солнца возникает в относительно тонком (порядка 700 км) внешнем слое, называемом фотосферой. Его эффективная температура порядка 6 000 К. Температура внутри Солнца превышает 107 К.
Кроме спокойного свечения на Солнце наблюдаются отдельные вспышки. Считают, что они представляют собой «разряды», обусловленные переменными полями в областях солнечных пятен. Солнечную радиацию в целом условно можно разделить на два типа: электромагнитные волны и заряженные частицы. Электромагнитные волны представляют собой ультрафиолетовые лучи, видимый свет и радиоволны. Заряженные частицы образуют так называемый солнечный ветер, скорость которого вблизи Земли достигает 400 км/с при концентрации частиц 1...10 протонов/см3. Потоки плазмы солнечного ветра увлекают за собой в межпланетное пространство и солнечные магнитные поля. Индукция этих полей вблизи орбиты Земли составляет около 5 нТл.
Общее количество энергии, излучаемой Солнцем в 1 с, составляет 3,86*1021 Дж. На долю Земли приходится одна двухмиллионная ее часть. Тем не менее за год Земля получает 6,1*1024 Дж, а за галактический год –
1,22*1033 Дж. Этой энергии вполне хватает для обеспечения протекания любых тектонических явлений на Земле.
1.2.2. Планеты Солнечной системы.
Планеты Солнечной системы принято делить на внутренние – Меркурий, Венера, Земля, Марс, и внешние – Юпитер, Сатурн, Уран, Нептун.
Для внутренних планет характерны сравнительно небольшие диаметр и сжатие; для внешних большие геометрические размеры и сжатие. В табл. 1.1 приведены основные параметры перечисленных выше планет.
Таблица 1.1
Основные параметры планет Солнечной системы
| Параметр | Меркурий | Венера | Земля | Марс | Юпитер | Сатурн | Уран | Нептун |
| Среднее расстояние от Солнца, млн. км | 57,9 | 108,2 | 149,6 | 227,9 | 778,3 | |||
| Период обращения, сут. | 224,7 | 365,26 | 687,0 | 30680 | 60190 | |||
| Период вращения, сут. | 58,6 | 243 (обр.) | 1,026 | 0,410 | 0,426 | 0,448 (обр.) | 0,658 | |
| Угол наклона оси | 28° | 3° | 23°27' | 23°59' | 3°05' | 26°44' | 82°5' | 28°48' |
| Угол наклона орбиты к эклиптике | 7°0' | 3°24' | 0° | 1°51¢ | 1°18' | 2°29' | 0°46' | 1°46' |
| Средний радиус, тыс. км | 2,439 | 6,05 | 6,371 | 3,39 | 69,72 | 57,9 | 24,54 | 25,0 |
| Масса, ед. массы Земли | 0,055 | 0,815 | 0,108 | 317,9 | 95,2 | 14,6 | 17,2 | |
| Объем, ед. объема Земли | 0,06 | 0,88 | 0,15 | |||||
| Средняя плотность, г/см3 | 5,4 | 5,2 | 5,52 | 3,9 | 1,3 | 0,7 | 1,2 | 1,7 |
| Сжатие, отн. ед. | 0,003 | 0,009 | 0,06 | 0,1 | 0,06 | 0,02 | ||
| Сила тяжести, ед. ст. на Земле | 0,37 | 0,88 | 0,38 | 2,64 | 1,15 | 1,17 | 1,17 |
Меркурий очевидно имеет дипольное магнитное поле, силовые линии которого направлены примерно вдоль оси вращения планеты. Индукция поля на поверхности планеты находится в пределах 350–700 нТл, что составляет 1 % напряженности магнитного поля на поверхности Земли. Полярность магнитного поля Меркурия совпадает с полярностью магнитного поля Земли.
Венера. Магнитное поле, если и существует, то по крайней мере в 104 слабее земного. Объясняют это малой скоростью ее вращения. Для Венеры характерна плотная атмосфера, наблюдаемые верхние слои которой испытывают глобальное вращение в направлении, обратном вращению планеты, с периодом порядка 4 сут. Природа этого явления пока не нашла объяснения.
Марс. Обладает магнитным полем, индукция которого на экваторе достигает ~64 нТл. Полярность обратная земной. Угол между осью диполя и осью вращения ~15°. Ось вращения Марса, в отличие от земной, меняет угол своего наклона на ~20° с периодом 105 и 106 лет. Одной из особенностей Марса является наблюдаемые на нем мощные пылевые бури, имеющие планетарный характер. Для образования пылевой бури необходима скорость ветра у поверхности свыше 150 км/ч.
Юпитер. Магнитное поле дипольное, полярность противоположна земной. Ось диполя наклонена к оси вращения на 100,8 и смешена от центра планеты на расстояние 700 км. Индукция магнитного поля в верхней части облачного слоя меняется от 3*10-4 до 14*10-4 Тл. Вблизи поверхности планеты поле становится более сложным: появляются квадрупольные и октопольные компоненты. Особенностью Юпитера является неравномерность вращения отдельных его частей: вблизи экватора «детали» вращаются с периодом 9 ч 50 мин. 30 с, а в высоких широтах – 9 ч 55 мин 41 с. Это расхождение объясняют крупномасштабными изменениями юпитерианских ветров.
1.3. Основные параметры и ротационный режим системы Земля – Луна
1.3.1. Земля.
Землю и ее спутник Луну можно рассматривать в качестве двойной планеты, вращающейся вокруг общего центра. Ниже приведены их основные параметры.
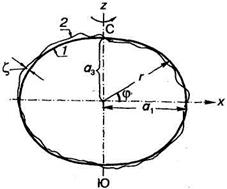
Масса Земли – 5,976*1024 кг, объем – 1,083*1021 м3. Реальная форма Земли очень сложна. В первом приближении ее можно считать эллипсоидом вращения (рис. 1.2). Экваториальный радиус земного эллипсоида а1=6,378160·103 км, полярный радиус а3=6,356778·103 км, радиус равновеликого шара а=6,371023*103 км. Сжатие земного эллипсоида 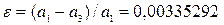 .
.
Уравнение земного эллипсоида можно записать в виде
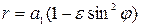
| (1.1) |
где r и 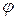 – полярные координаты точек земного эллипсоида.
– полярные координаты точек земного эллипсоида.
В качестве следующего приближения к реальной форме Земли принимают геоид. Геоид представляет собой одну из уровенных поверхностей гравитационного потенциала Земли, совпадающей с невозмущенной поверхностью морей и океанов, продолженную под континенты. Эта поверхность наиболее близко совпадает с земным эллипсоидом, отклоняясь от него не более чем на 120 м. В геодезической практике геоид используется для восстановления истинной поверхности Земли.
|
Рисунок 1.2 - К определению формы Земли
1 – земной эллипсоид, 2 – геоид, 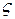 – превышения геоида над эллипсоидом.
– превышения геоида над эллипсоидом.
Из других параметров Земли назовем геоцентрическую гравитационную постоянную и моменты инерции. Геоцентрическая гравитационная постоянная, представляющая собой произведение гравитационной постоянной f на массу Земли, включая ее атмосферу, m,
fm = (3,98603 ±0,00003)*1014 м3/с2.
Моменты инерции: экваториальный А = 8,042*1044 г*см2; полярный
С = 8,068*1044 г*см2, средний I = 1/3(2A+С).
Моменты инерции необходимы для изучения внутреннего строения Земли.
1.3.2. Ротационный режим Земли.
Рассмотрим четыре параметра ротационного режима Земли: прецессию и нутацию земной оси вращения, изменение положения оси вращения (полюсов) по отношению к земной поверхности и изменение угловой скорости вращения Земли  .
.
Прецессия – это медленное движение оси вращения Земли по круговому конусу. Ось этого конуса перпендикулярна плоскости земной орбиты, а угол между осью и образующей конуса равен 23°27'. Период прецессии составляет 25 765 лет.
Еще во II веке до н.э. греческий астроном Гиппарх обнаружил, что точка весеннего равноденствия медленно перемещается относительно звезд навстречу годичному движению Солнца. Благодаря тому, что равноденствие наступает раньше, чем Солнце совершает полный оборот по эклиптике, явление получило название предварения равноденствий, или прецессии.
Колебание оси вращения Земли влечёт изменение положения звёзд относительно экваториальной системы координат. В частности, через некоторое время Полярная звезда перестанет быть ближайшей к северному полюсу Земли яркой звездой, а Турайс будет Южной Полярной звездой примерно в 8100 году н. э.
Прецессионное движение земной оси в основном вызвано притяжением Луны и Солнца, а также неоднородностью плотности распределения масс внутри Земли.
Нутация – небольшие колебания земной оси, накладывающиеся на равномерное прецессионное движение
Нутация земной оси складывается из движений с различными периодами, максимальный из них равен 18,6 года. Максимальное отклонение земной оси от среднего положения достигает 9",21.
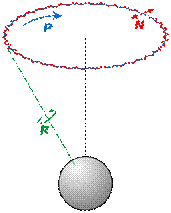
Рисунок 1.3 - Вращение (R), прецессия (P) и нутация (N) планеты
Изменение положения оси вращения (полюсов) по отношению к земной поверхности. Точки, в которых ось пересекает земную поверхность (мгновенные полюса Земли), постоянно перемещаются по земной поверхности вокруг среднего полюса в направлении вращения Земли, то есть с запада на восток. Траектория движения полюса имеет вид спирали, которая периодически то закручивается, то раскручивается. Для примера на рисунке 1.4 показана траектория движения мгновенного Северного полюса за 1996−2000 гг. Его максимальное удаление от среднего отмечалось в мае-июле 1996 г. Затем полюс стал закручиваться, и это продолжалось до 2000 г., когда он подошел на минимальное расстояние к центру спирали. Сейчас полюс раскручивается и удаляется от своего среднего положения.
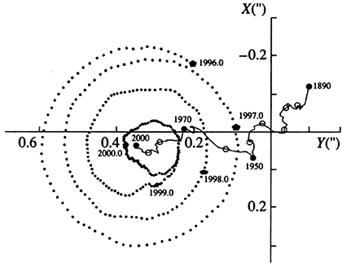
Рисунок 1.4 - Траектория движения мгновенного Северного полюса за 1996−2000 гг.
Самое большое удаление мгновенного полюса от среднего не превышает 15 м. Закручивание и раскручивание траектории полюса объясняется тем, что он совершает два периодических движения: свободное или чандлеровское (названо в честь открывшего его в 1891 г. С. Чандлера) с периодом около 14 месяцев и вынужденное – с годовым периодом. Чандлеровское движение полюсов возникает, если ось вращения Земли отклонена от оси ее наибольшего момента инерции. Движение полюсов, вызванное действием на Землю периодических сил атмосферы и гидросферы, называется вынужденным – именно его и привносят землетрясения и цунами. Период свободного движения зависит не от периода возбуждающей силы, как это характерно для вынужденного движения, а от динамического сжатия и упругих свойств планеты. Сложение этих движений и дает наблюдаемую картину.
Изменение угловой скорости вращения Земли  . В большом масштабе времени угловая скорость вращения Земли постоянно замедляется.
. В большом масштабе времени угловая скорость вращения Земли постоянно замедляется.
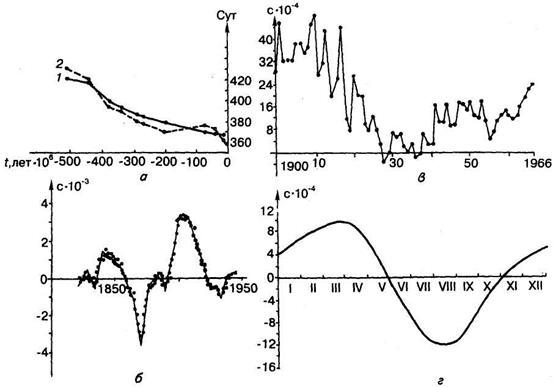
На рис. 1.5, а приведены графики изменения угловой скорости вращения Земли в течение фанерозоя, выраженной количеством суток в астрономическом году. Однако это замедление происходит не линейно, а нарушается периодическими и нерегулярными колебаниями угловой скорости, представление о которых можно получить из графиков, приведенных на рис. 1.3, б, в. График изменения продолжительности года в течении суток приведен на рис. 1.3 г.
|
Рисунок 1.5 – Графики изменения угловой скорости Земли:
а – графики изменения числа дней в году (1 – по замерам астрономического года, 2 – по замерам синодического месяца); б – график изменения продолжительности суток с 1825 по 1950 г.; в – изменение среднегодовой продолжительности суток с 1900 по 1966 г.; г – вид кривых колебания продолжительности суток в течение года.
1.3.3. Луна и приливы на Земле.
Параметры Луны: масса – 7,35*1022 кг, средний радиус – 1738 км, средняя плотность – 3340 кг/м3, период вращения (сидерический месяц) – 27,323661 сут. Луна обращается вокруг Земли по эллиптической орбите, большая полуось которой равна 384,4*103 км, а малая – на 21*103 км меньше. Плоскость орбиты Луны наклонена к эклиптике на угол 5°,9. Характерной особенностью орбиты Луны является непрерывное изменение ее основных характеристик (полуосей эллипса и угла наклона плоскости лунной орбиты к эклиптике), происходящее под действием возмущений, обусловленных притяжением Солнца и других планет, а также отклонениями форм Земли и Луны от сферической. Все это приводит к изменениям условий взаимодействия Земли и Луны.
Под влиянием лунного притяжения в Земле возникают своеобразные приливы, проявляющиеся в виде подъемов и сопутствующих им опусканий земной поверхности на материках или водной поверхности в акваториях морей и океанов, волнообразно перемещающихся по поверхности Земли вслед за движением Луны (рис. 1.4, а). Сложность траектории Луны обусловливает также сложный характер приливных движений в земной коре. Их можно представить состоящими из совокупности волн с периодами, начиная от долей суток и кончая многолетними. Наиболее четко проявляются волны с полусуточными, суточными и двухнедельными периодами. Согласно теоретическим расчетам, для Земли, обладающей свойствами идеальной жидкости, под влиянием лунного притяжения уровневая поверхность Земли (геоид) могла бы подняться максимум на 35,6 см, а опуститься – максимум на 17,8 см, т.е. диапазон колебаний мог бы составить 53,4 см. На лунные приливные деформации геоида накладываются аналогичные солнечные, диапазон изменения которых несколько меньше. Он составляет 24,6 см. Следовательно, суммарное лунно-солнечное влияние может привести к максимальным колебаниям геоида в 78 см. Реальные изменения геоида, в связи с реологическими свойствами верхних оболочек Земли, составляют всего 65 % от приведенной выше величины, т.е. ~51 см.
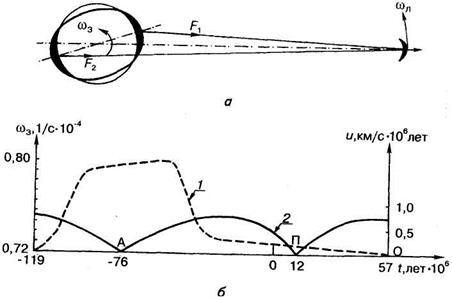
Рисунок 1.4 – Схема образования приливов в Земле (а)
и их роль в изменении угловой скорости вращения Земли (б):
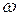 – угловая скорость вращения Земли;
– угловая скорость вращения Земли; 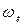 – угловая скорость обращения Луны вокруг Земли;
– угловая скорость обращения Луны вокруг Земли; 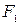 и
и 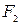 – силы взаимодействия приливных волн с Луной, разность которых создает момент, приводящий к изменению угловой скорости вращения Земли; 1 – изменение угловой скорости вращения Земли;
– силы взаимодействия приливных волн с Луной, разность которых создает момент, приводящий к изменению угловой скорости вращения Земли; 1 – изменение угловой скорости вращения Земли;
2 – изменение ускорения движения Солнца вокруг центра Галактики;
А – апогалактий; П – перигалактий; О – современная эпоха.
1.3.4. Приливы и изменения угловой скорости вращения Земли.
Описанные выше изменения скорости движения Солнца по галактической орбите приводят к закономерному изменению ее круговой скорости обращения. Последняя, в свою очередь, влияет на изменение скорости обращения Луны вокруг Земли, точнее вокруг их общего барицентра.
Первое относительное изменение скорости обращения Луны должно происходить по тем же причинам, по которым изменяется круговая скорость обращения Земли, т.е. в результате уменьшения скорости поступательного движения системы Земля – Луна за время перемещения от апогалактия к перигалактию, как и се увеличение при движении Солнечной системы в обратном направлении. Второе относительное изменение скорости обращения Луны должно происходить в том же масштабе в результате увеличения круговой скорости движения Земли (также и барицентра).
Таким образом, при прохождении Солнечной системы через апогалактий орбитальная круговая скорость Луны должна быть максимальной, а при прохождении через перигалактий – минимальной. Орбитальная круговая скорость Луны должна испытывать периодические колебания, аналогичные колебаниям орбитальной круговой скорости Солнца с тем же периодом, но в противоположных фазах. При этом в течение аномалистического периода (176*106 лет) угловая скорость обращения Луны изменится от значений больших угловой скорости вращения Земли до значений меньших ее и наоборот. Дважды они оказываются равными между собой.
В связи с определенными реологическими свойствами верхних оболочек Земли экстремумы главных приливных волн оказываются смешенными от оси Земля – Луна. Направление этого смещения определяется соотношением угловых скоростей вращения Земли 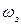 и обращения Луны вокруг барицентра Земля – Луна
и обращения Луны вокруг барицентра Земля – Луна 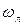 . При смещении экстремумов приливных волн от линии Земля – Луна в направлении вращения Земли под действием лунного притяжения образуется пара сил, тормозящая вращение Земли, а при смещении в обратном направлении возникает момент сил, ускоряющий вращение Земли
. При смещении экстремумов приливных волн от линии Земля – Луна в направлении вращения Земли под действием лунного притяжения образуется пара сил, тормозящая вращение Земли, а при смещении в обратном направлении возникает момент сил, ускоряющий вращение Земли
(см. рис. 1.4, а).
На рис. 1.4, б приведены кривые изменения скорости вращения Земли и ускорения движения Солнца за аномалистический период. Обращает на себя внимание асимметричный вид кривой изменения скорости вращения Земли. Это связано с эксцентриситетом лунной орбиты. Дело в том, что во время увеличения скорости вращения Земли расстояние между Землей и Луной значительно меньше, чем в период замедления. В связи с этим период замедления составляет приблизительно 108*106 лет, а период ускорения – 68*106 лет.
Описанный выше эффект влияния приливов на изменение угловой скорости вращения Земли обусловлен колебанием наибольшего момента инерции Земли, что приводит к последовательной периодической смене ускорений и замедлений вращения Земли с общей тенденцией к ее замедлению. На этот процесс накладываются значительно более слабые эффекты векового замедления Земли, связанные с диссипацией энергии вследствие приливных деформаций земной коры, а также тормозящее влияние солнечных приливов.
В заключение укажем, что результаты изучения влияния приливов в Земле на угловую скорость ее вращения объясняют основную тенденцию последней к уменьшению (см. рис. 1.4, а), но это уменьшение происходит не плавно, а нарушается периодическими колебаниями.
2. ФИЗИЧЕСКИЕ ПОЛЯ ВНУТРЕННЕЕ СТРОЕНИЕ ЗЕМЛИ
2.1. Оболочечное строение Земли
2.1.1. Скорости распространения упругих волн в Земле.
В общих чертах Землю представляют состоящей из следующих концентрических слоев:
1) тонкой коры, структура которой переменна и относительно сложна;
2) менее неоднородной твердой мантии, простирающейся от коры до глубины порядка 2900 км;
3) жидкого внешнего слоя ядра толщиной около 2200 км;
4) вероятно твердого внутреннего ядра радиусом порядка 1200 км. Такие представления основаны на результатах изучения закономерностей распространения в Земле упругих волн, вызванных землетрясениями.
На рис. 2.1, а приведены графики изменения скоростей продольных и поперечных упругих волн от поверхности Земли до ее центра.
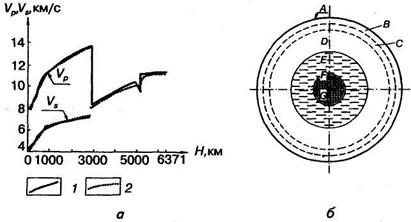
Рисунок 2.1 – Графики распределения скоростей продольных 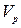 и поперечных
и поперечных 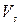 упругих волн в Земле (а) и соответствующие им концентрические оболочки (зоны) Земли (б)
упругих волн в Земле (а) и соответствующие им концентрические оболочки (зоны) Земли (б)
Рядом исследователей предложены модели строения Земли, в основе которых лежат приведенные выше трафики рас пространения упругих волн. Они отличаются только деталями. Поэтому ниже рассмотрена одна из них (тип А), составленная К.Е. Булленом. Согласно этой модели Земля разбита на семь концентрических оболочек (зон), которым присвоены буквенные обозначения: A, B, C, E, F, G. На рис. 2.1, б показана схема расположения названных оболочек Земли (с сохранением относительного масштаба), а в табл. 2. приведены физические параметры этих оболочек. Параметры упругих свойств вещества зон получены, в основном, по данным сейсмологии. При определении плотности использовалось соотношение между скоростью распространения упругих волн в веществе и его плотностью с тем условием, чтобы удовлетворились известные значения средней плотности Земли и ее момента инерции.
Таблица 2 – Параметры модели строения Земли (тип А)
| Зона | Интервал глубин, км | Интервал плотности, г/см3 | Модуль Юнга E×1011, Н/м2 | Коэффициент Пуассона | Давление Р×1011, Н/м2 | |
| Кора | A | 0-33 | (2,84) | (0,91) | (0,267) | 0-0,009 |
| Мантия | В | 33-413 | 3,32-3,64 | 1,60-2,29 | 0,270-0,280 | 0,009-0,141 |
| С | 413-984 | 3,64-4,55 | 2,29-4,68 | 0,280-0,276 | 0,141-0,379 | |
| D | 984-2000 | 4,55-5,11 | 4,68-6,33 | 0,276-0,293 | 0,379-0,87 | |
| Ядро | E | 2998-4000 | 9,98-11,42 | 0,5 | 1,36-2,47 | |
| 4000-4980 | 11,42-12,17 | 0,5 | 2,47-3,20 | |||
| F | 4980-5120 | 12,17-12,25 | - | - | 3,20-3,28 | |
| G | 5120-6371 | 12,25-12,51 | - | - | 3,28-3,61 |
*Значения параметров даны условно
2.1.2. Характеристики зон.
Зона А представляет собой земную кору. В качестве подошвы коры принимают сейсмическую границу Мохоровичича, в окрестности которой происходит изменение скорости продольных упругих волн от 7 до 8 км/с. Это наименее однородная зона. Детально она будет рассмотрена в следующем разделе.
Зоны B, C и D соответствуют мантии Земли. Резкой разницы между ними нет, за исключением того, что в интервале зоны Г наблюдаются повышения значений градиентов нарастания скоростей VP и VS, с глубиной. Границы между зонами соответствуют скачкам этих значений. С зоной В исследователи часто связывают наличие слоя (слоев) «пониженной скорости» и соответствующего ему слоя «инверсии плотности». Эти слои обычно отождествляются с астеносферой, играющей существенную роль в геотектонических построениях. Вопрос о существовании гипотетической астеносферы рассмотрен ниже. К. Е. Буллен, исходя из современных данных, пришел к выводу, что существование слоев пониженной плотности следует считать вполне возможным, но вовсе не доказанным.
Совокупность зон В и С обычно называют верхней мантией, а D - нижней мантией.
Зоны Е, F и G – соответствуют ядру Земли. Зону Е называют внешним ядром. В связи с тем, что сквозь эту зону не проходят поперечные волны, сделан вывод, что вещество в нем находится в жидком состоянии. Большую часть зоны Е рассматривают как достаточно однородную. Согласно теории динамомагнитного поля Земли, зона Е – сосредоточение конвективных потоков, которые создают главную часть магнитного поля.
Зону G – внутреннее ядро – считают твердым, сложенным достаточно однородным веществом.
Зона F – переходный слой между внешним и внутренним ядром – характеризуется наличием резкого скачка в скорости распространения продольных упругих волн.
2.1.3. Состав земных недр.
Проблема состава земных недр в настоящее время является одной из самых сложных, поскольку прямых данных о породах в подкоровом пространстве нет. Исследователи вынуждены ограничиваться гипотезами, основанными на косвенных данных. В частности, полезной является аналогия с составом метеоритов. Известны два класса метеоритов: «железные», состоящие преимущественно из железо-никелевого сплава, и «каменные», состоящие главным образом из силикатов. Каменные метеориты разделяют на две группы: хондриты (-90 %) и ахондриты (- 10%). Состав хондритов удивительно однообразен и подобен составу ультра основных пород на Земле; состав ахондритов – ближе к базальтам. В первом приближении принимается, что состав ядра подобен составу железных метеоритов, а состав мантии – каменных (хондритов). Дальнейшее уточнение состава обычно осуществляется на основании экспериментальных данных о свойствах соответствующих горных пород при высоких температурах и давлениях. Проблема осложняется тем, что до сих пор окончательно не решен вопрос о «горячем» или «холодном» происхождении Земли, хотя большинство исследователей склоняются к представлениям о «холодном» ее происхождении. При этом в качестве механизма образования внутренних оболочек Земли можно принять гипотезу зонной плавки, предложенную А.П. Виноградовым. Отличительной особенностью гипотезы зонной плавки от аналогичной гипотезы гравитационной дифференциации является то, что в процессе зонной плавки вверх поднимаются не более легкие, а более легкоплавкие компоненты.
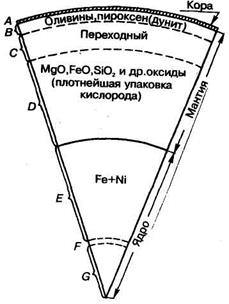
На рис. 2.2 приведен состав отдельных зон Земли в соответствии с гипотезой зонной плавки. Обсуждая этот же вопрос, К.Е. Буллен считает, что зоны B и D можно принять однородными по химическому и фазовому составам. Некоторое отличие зоны С он связывает с фазовыми переходами, а изменение состава считает малым. Химический и фазовый составы в зонах Е и G он также считает одинаковыми, но не чисто Fe-Ni Различные исследователи наряду с Ре и Ni включают в ядро Si, Мg, О, S. Отдается предпочтение представлениям, согласно которым ядро (во всяком случае внешнее) состоит из 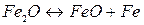 .
.
|
Рисунок 2.2 – Разрез Земли
2.1.4. Гидросфера и атмосфера.
Представление об оболочечном строении Земли было бы не полным, если не отмстить существование гидросферы и атмосферы. Гидросфера занимает около 70 % площади поверхности Земли. Она является составной частью земной коры. Более того, ряд исследователей земную кору акваторий морей и океанов выделяют в особый тип и используют ее для объяснения тектонических процессов на Земле. Поэтому этот вопрос будет более детально рассмотрен в следующем разделе.
Что касается атмосферы, то она, в свою очередь, состоит из нескольких диффузионно разделенных слоев (начиная от поверхности Земли): тропосфера, в которой сосредоточено ~79 % всей массы атмосферы; стратосфера
~20 %; ионосфера ~0,5 % и верхняя атмосфера – слой водорода, переходящий в межпланетную среду. Границы между этими «сферами» выражены не резко, а их форма повторяет сплюснутость Земли. В атмосфере так же, как в гидросфере и твердой Земле наблюдаются приливы. Атмосфера играет существенную роль в преобразовании солнечной энергии и в определении экзогенных геологических процессов на Земле.
2.2. Гравитационное поле Земли и концепция изостазии
2.2.1. Гравитационное поле.
Одной из основных характеристик гравитационного поля является его напряженность или соответствующая ей величина ускорения силы тяжести. Величину ускорения силы тяжести на поверхности Земли получают разными способами: прямым измерением приборами; вычислениями, в которых используется теория движения искусственных спутников в гравитационном поле Земли и др.
Величина ускорения силы тяжести на поверхности Земли состоит из двух составляющих. Одна из них обусловлена притяжением масс Земли, а вторая – центробежной силой вращения Земли вокруг собственной оси. Совокупное действие этих сил приводит к сжатию Земли. Величина сжатия определяется соотношением
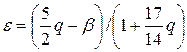
| (2) |
где q=1/289 – отношение центробежной силы к силе тяжести на экваторе (gэ);
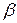 – отношение разности силы тяжести на полюсе и на экваторе к силе тяжести на экваторе.
– отношение разности силы тяжести на полюсе и на экваторе к силе тяжести на экваторе.
Выражение нормального ускорения силы тяжести g0 для земного эллипсоида (эллипсоида Клеро) имеет вид
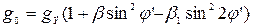
| (3) |
где 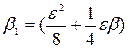 ;
;
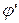 – геодезическая широта.
– геодезическая широта.
В 1971 г. Международным союзом геофизики и геодезии была рекомендована следующая формула для вычисления нормального значения ускорения силы тяжести:
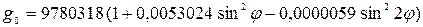
| (4) |
где 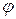 – географическая широта.
– географическая широта.
Отклонения наблюдаемых (или вычисленных) значений ускорения силы тяжести от нормальных называют аномалиями 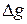 . Аномалии обусловлены плотностными неоднородностями в Земле. Они создают небольшие отклонения уровенной поверхности гравитационного потенциала от земного эллипсоида, превращая его в геоид.
. Аномалии обусловлены плотностными неоднородностями в Земле. Они создают небольшие отклонения уровенной поверхности гравитационного потенциала от земного эллипсоида, превращая его в геоид.
Геоид – это уровенная поверхность гравитационного потенциала, наиболее близко совпадающая с земным эллипсоидом и перпендикулярная в каждой точке вектору силы тяжести. Отклонения геоида от земного эллипсоида 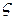 , можно вычислять по формуле Стокса:
, можно вычислять по формуле Стокса:
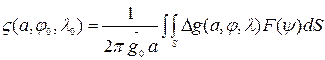
| (5) |
где а, 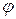 ,
, 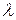 – сферические координаты переменной точки на поверхности Земли, принятой за сферу радиусом а;
– сферические координаты переменной точки на поверхности Земли, принятой за сферу радиусом а;
а, 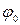 ,
, 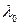 – сферические координаты точки исследования;
– сферические координаты точки исследования;
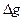 (а,
(а, 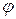 ,
, 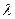 ) – аномалии ускорения силы тяжести;
) – аномалии ускорения силы тяжести;
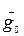 – среднее нормальное значение ускорения силы тяжести на поверхности Земли;
– среднее нормальное значение ускорения силы тяжести на поверхности Земли;
dS – элемент поверхности Земли;
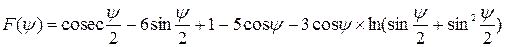 – функция Стокса;
– функция Стокса;
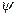 определяется из уравнения
определяется из уравнения 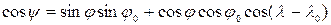 .
.
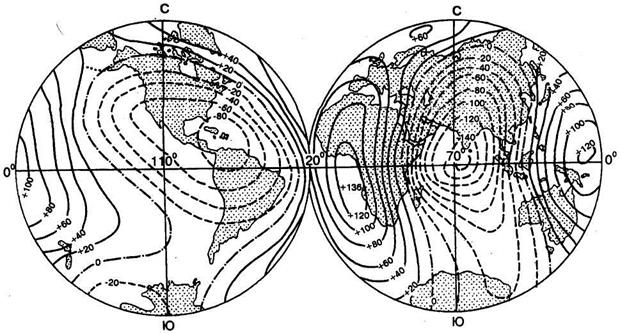
На рис. 2.3 приведена карта высот геоида, вычисленная таким способом.
|
Рисунок 2.3 – Карта высот геоида
2.2.2. Концепция изостазии.
Аномалии ускорения силы тяжести, обусловленные неоднородностями в Земле, осложняя поверхность земного эллипсоида, приводят к уклонению вертикалей от их нормального положения (уклонению отвесных линий). Вертикали имеют существенное значение в геодезии и астрономии, поскольку от них отсчитываются угловые расстояния в сферических координатах. Уклонения линий можно вычислять по распределению аномалий 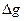 на поверхности Земли, но в процессе решения этой проблемы исследователи еще в прошлом веке столкнулись с любопытным фактом. Вычисленные значения влияния избыточных масс близлежащих гор и дефекта масс в океане оказались существенно больше наблюдаемых. Для объяснения этого факта была принята гипотеза, согласно которой под горными сооружениями наблюдается разуплотнение вещества, компенсирующее влияние массы горы, а под океанами – уплотнение вещества, компенсирующее дефект масс в океане (по отношению к окружающим его горным породам). Так возникло учение об изостазии.
на поверхности Земли, но в процессе решения этой проблемы исследователи еще в прошлом веке столкнулись с любопытным фактом. Вычисленные значения влияния избыточных масс близлежащих гор и дефекта масс в океане оказались существенно больше наблюдаемых. Для объяснения этого факта была принята гипотеза, согласно которой под горными сооружениями наблюдается разуплотнение вещества, компенсирующее влияние массы горы, а под океанами – уплотнение вещества, компенсирующее дефект масс в океане (по отношению к окружающим его горным породам). Так возникло учение об изостазии.
Во время возникновения концепции изостазии в соответствии с господствующими тогда представлениями о «плавлении» земной коры на магме, изучение равновесного состояния Земли было заменено изучением равновесного состояния земной коры. Такой подход, по-существу, сохраняется до сих пор, только оценивают равновесное состояние не земной коры, а литосферы. В последнем случае роль подстилающей кору магмы играет гипотетическая астеносфера. Под изостатическим состоянием земной коры (литосферы) понимают такое ее состояние, при котором она располагается на субстрате так, как если бы она плавала на нем по закону Архимеда. Естественным следствием такого предположения является равенство давлений на некоторой поверхности в субстрате (закон Паскаля), называемой поверхностью компенсации.
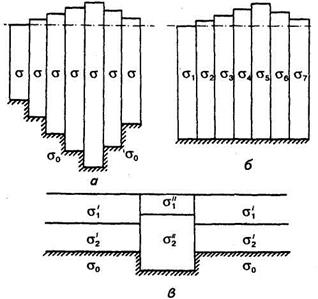
Для практического учета влияния масс, распределенных в земной коре согласно гипотезе изостазии, пользуются различными физико-геологическими моделями, сущность которых видна из рис. 2.4, а, б. Подчеркнем, что каждый фрагмент модели считается уравновешивающимся самостоятельно (локальная компенсация). Ф.А. Венинг-Мейнец предложил гипотезу региональной компенсации, учитывающей взаимное сцепление блоков земной коры. Однако способ расчета изостатического влияния существенно не изменился. Вычисленное с помощью названных выше моделей гравитационное влияние изостатически распределенных масс в верхней части земной коры вводилось в качестве поправок (редукций) в аномалии 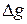 . Полученные таким образом аномалии были названы изостатическими. В основе всех использованных моделей лежит предположение, что распределение масс в земной коре и, следовательно, ее уравновешенность определяются только рельефом земной поверхности.
. Полученные таким образом аномалии были названы изостатическими. В основе всех использованных моделей лежит предположение, что распределение масс в земной коре и, следовательно, ее уравновешенность определяются только рельефом земной поверхности.
Г.Я. Голиздрой развита концепция изостазии равнинных областей, в которой за основу принято тоже равновесное состояние земной коры, но в качестве уравновешивающих факторов наряду с топографическими массами используются неоднородности в верхних частях земной коры, установленные сейсмическими методами. В условиях равнинных областей второй фактор приобретает решающее значение. Одна из моделей, используемых им для оценки изостатического состояния земной коры, приведена на рис. 12, в. В частности, им показано, что в условиях равнинного рельефа Украинского щита при наличии поверхностных неоднородностей в верхних частях земной коры, создающих аномалии гравитационного поля в несколько десятков миллигал, состояние земной коры в целом близко к изостатическому. Следовательно, топографические массы не только не могут быть единственным фактором, определяющим изостатическое состояние земной коры, что признается уже многими исследователями, а, как будет показано ниже, их нельзя считать и основными.
|
Рисунок 2.4 – Физико-геологические модели изостазии земной коры: а — Г. Эри; б — Ф.Драпа; в — Г.Я. Голиздры; s0 — плотность субстрата; s — плотность уравновешенных блоков разной высоты по Г. Эри; s1, s2,… s7 –тоже по Ф. Пратту; s¢1, s¢¢1 — плотность блоков гранитного слоя земной коры; s¢1, s¢¢2 — то же, базальтового слоя по Г.Я. Голиздре
Изостатические аномалии в классическом варианте оказались весьма полезными при решении астрономо-геодезических задач, в частности, при определении уклонения отвеса. Неоднократно предпринимались попытки использования концепции изостазии для создания геотектонических гипотез развития Земли. Детальный обзор ранних предложений сделан Е.Н. Люстихом. В настоящее время можно констатировать следующее. Несмотря на, казалось бы, естественную взаимосвязь между перераспределением масс в литосфере и тектоникой, установить конкретную роль изостатических сил в формировании тектонических структур пока не удалось. Наблюдающиеся в различных геологических регионах современные движения земной поверхности происходят как в направлении выравнивания равновесного состояния земной коры, так и наоборот. Единственной устойчивой закономерностью считают прямую взаимосвязь между нарушениями изостазии земной коры, вычисленной с помощью одной из приведенных выше моделей, и современной тектонической активностью отдельных регионов.
Следует специально подчеркнуть, что рассмотренная выше концепция изостазии земной коры (литосферы) предполагает ротационный режим Земли постоянным, а соответствующую ему фигуру равновесия — неизменной.
Ниже приведены данные о средних значениях ускорения силы тяжести внутри Земли (табл. 2.2).
Таблица 2.2 - Распределение ускорения силы тяжести в Земле
 Интервал глубин, км Интервал глубин, км
| 33-413 | 413-984 | 984-2000 | 2000-2998 | 2998-4000 | 4000-4980 | 4980-5120 | 5120-6371 | |
| Интервал значений g, м/с2 | 9,822 | 9,846-9,960 | 9,960-9,966 | 9,966-10,01 | 10,01-10,73 | 10,73-7,87 | 7,87-4,78 | 4,78-4,31 | 4,31-0 |
2.3. Тепловое поле Земли
2.3.1. Общие сведения
Представления о тепловом поле внутри Земли одни из самых проблематичных, поскольку они основываются на интерпретации фактических данных, относящихся к поверхности Земли. Вследствие многозначности этой интерпретации, описываемые ниже закономерности оказываются тоже во многом гипотетичными. Вместе с тем, тепловое поле Земли может быть прямо или косвенно причастно к протеканию тектонических процессов на Земле. Поэтому сведения о тепловом поле необходимы. Ниже приведены данные
(табл. 2.3) об энергетических процессах, в которых участвует Земля.
Из таблицы следует, что самое большое количество энергии Земля получает от Солнца, но значительная ее часть теряется в атмосфере. Средний поток солнечной теплоты, достигающий поверхности Земли на континентах, порядка 42*104 Вт/м2, по сравнению с потоком теплоты из недр Земли
(62 Вт/м2) все еще достаточно велик, но основная его часть через атмосферу вновь излучается в пространство. Лишь малая доля солнечной энергии проникает на глубину, измеряемую метрами.
В настоящее время принято считать, что главным источником современной тепловой энергии в недрах Земли является радиоактивный распад долгоживущих изотопов. На ранних этапах истории Земли существенную роль в тепловых процессах могла играть освобождающаяся гравитационная энергия. Основной характеристикой теплового поля Земли является поток теплоты через земную поверхность. Тепловой поток через единицу площади поверхности Q определяется произведением градиента температуры на коэффициент теплопроводности. Первый измеряется в натуре на материках в скважинах и горных выработках, в океане – в придонных частях, а второй – на образцах горных пород или in situ. В данном случае это подчеркивается потому, что таким образом учитывается только кондуктивная составляющая теплового потока.
Таблица 2.3 – Основные составляющие энергетического баланса Земли
| Вид энергии | Е, Дж/год |
| Солнечная энергия (получаемая и переизлучаемая обратно) | 1025 |
| Геотермическая потеря теплоты | 1021 |
| Энергия, теряющаяся при замедлении вращения Земли | 3×1025 |
| Упругая энергия, высвобождающаяся при землетрясениях | 1018 |
2.3.2. Распределение теплового потока
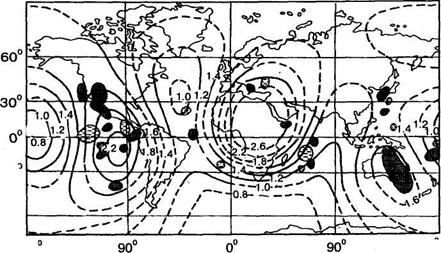
На рис. 2.5 приведена карта теплового потока. Она дает общее представление о глобальном распределении теплового потока. Основной вывод, который можно сделать из анализа этой карты – нет никакой корреляции между «повышениями» и «понижениями» теплового потока и основными поверхностными образованиями Земли – континентами и океанами.
Распределение теплового потока в континентальных и океанических областях находится в тесной корреляции с основными геологическими структурами (табл. 2.4).
На континентах минимальные значения теплового потока с минимальными его вариациями характерны для щитов. Значениями выше среднего теплового потока характеризуются послепалеозойские орогенические регионы и области третичных вулканов. У молодых орогенических поясов средний тепловой поток увеличен, но в этих областях наблюдаются некоторые отклонения, значительно выходящие за рамки средних. Во многом аналогичная картина наблюдается и в океанических хребтах. Им свойственны значительные вариации теплового потока при большом среднем значении; максимальные значения потока в некоторых точках хребтов достигают 335 Вт/м2. В противоположность этому тепловой поток на крыльях океанических хребтов обычно меньше среднего. В океанических котловинах тепловой поток относительно невелик и распределен равномерно. Наименьшие средние значения теплового потока в океане отмечаются в глубоководных желобах.
|

Рисунок 2.5 – Распределение теплового потока на поверхности Земли:
1 – изолинии теплового потока, мккал/(см2×с); 2, 3 – локальные аномалии теплового потока, превышающие 2,0 (2) и меньше 1,0 мккал/(см2×с) (3).
Таблица 2.4 – Статистика результатов измерений теплового потока в основных геологических подразделениях континентов и океанов
| Геологическое подразделение | Число измерений, шт. | Средний тепловой поток, Вт/м2 |
| Континент | ||
| Докембрийские щиты | 38,5 | |
| Последокембрийские неорогенические области | 64,5 | |
| Орогенические области палеозоя | 51,5 | |
| Орогенические области мезозоя третичного периода | 80,4 | |
| Вулканические области третичного периода (без геотермальных районов) | 90,4 | |
| Океан | ||
| Океанические котловины | 53,6 | |
| Подводные хребты | 76,2 | |
| Глубоководные желоба | 41,5 | |
| Другие океанические области | 71,6 |
2.3.3. Перенос теплоты в Земле
Одна из центральных проблем земного теплового потока состоит в объяснении механизма выноса теплоты из недр Земли. Большая часть теряемой Землей теплоты достигает ее поверхности посредством теплопроводности пород земной коры. Однако здесь возникает проблема, которая в изложении М. Ботта представляется так. Если принять тепловой поток равным 62 Вт/м2 и теплопроводность 2,512 Вт/(м*К), то геотермический градиент получится равным 25 °С/км. При сохранении такого градиента температура на глубине 100 км должна достигать 2500 °С, а значит вызывать обширное плавление. Поэтому до того, как достичь 100 км, геотермический градиент должен уменьшиться примерно в 10 раз. Выполаживание кривой зависимости температуры от глубины можно объяснить либо концентрированием внутренних источников теплоты вблизи поверхности Земли, либо более эффективным механизмом переноса теплоты, чем простая теплопроводность, либо совместным действием этих факторов.
При температурах выше 800–1500 °С значительное количество теплоты передается через породу лучеиспусканием. В результате лучистого переноса коэффициент теплопроводности увеличивается на дополнительную
величину Кr. Величина Кr в значительной степени определяется прозрачностью силикатных минералов к несущим тепловую энергию красным лучам видимой области спектра и инфракрасным лучам. Кr является кубической функцией температуры.
Возможен и другой механизм переноса теплоты увеличивающий теплопроводность при высоких температурах. Теплота может передаваться «экситонами» – атомами, возбужденными радиацией. Надо полагать, что интенсивность экситоновой теплопроводности соизмерима с лучистой теплопроводностью. Вполне вероятно, что эффективная теплопроводность верхней мантии глубже 100 км на порядок выше, чем у поверхности. Поэтому геотермический градиент на этих глубинах меньше. Увеличение теплопроводности с глубиной может прекратиться в переходной зоне мантии и ниже из-за увеличения непрозрачности.
Существует гипотеза о наличии тепловой конвекции в Земле. Тепловая конвекция в жидкой среде может вынести наверх большое количество теплоты даже при сравнительно небольшом температурном градиенте. По-видимому, именно конвекцией передается теплота вверх через внешнее ядро.
2.3.4. Оценка температур внутри Земли.
Экстраполяция теплового потока у поверхности Земли дает некоторые сведения о распределении температуры в верхнем 50-км слое мантии. Ниже этого слоя сведения о температуре не достоверны, хотя можно установить для нее некоторые ограничения, исходя из известных физических свойств мантии.
Важный вывод можно сделать и относительно геотермического градиента. Начиная с глубин порядка 60 км, он должен существенно уменьшаться с глубиной. В противном случае температура на глубинах порядка 100 км превысит температуру плавления наиболее тугоплавкого оливина. На поверхности оливин плавится при 1900 °С, а при давлении 5 ГПа (глубина порядка 160 км) – при 2140 °С. По-видимому, это абсолютный верхний предел температуры верхнего слоя мантии. Более вероятный предел температуры определяется температурой образования базальтовой магмы при частичном плавлении ультраосновных пород. На глубине порядка 100 км она составляет 1300 °С, а на глубине 350 км – 2000 °С. Таким образом, большая часть магмы (если не вся) должна формироваться в верхней мантии. В районах активного вулканизма (Гавайские острова, Камчатка) магма образуется на глубинах порядка 60 км. Температура на этих глубинах, по-видимому, достигает 1250–1300 °С.
2.4. Магнитное поле Земли
2.4.1. Современное магнитное поле
В первом приближении геомагнитное поле представляют полем магнитного диполя, помещенного в центр Земли (гипотеза центрального диполя). Магнитный момент такого диполя характеризуется величиной порядка
8·1022 А*м2, а его ось наклонена на 11°,5 к оси вращения Земли. Считают, что лучшее приближение к наблюдаемому геомагнитному полю дает диполь, расположенный в магнитном центре Земли (гипотеза эксцентричного диполя
Наблюдаемое магнитное поле на поверхности Земли Т является суммой полей, имеющих различные причины возникновения:
Т= То+ Тт+ Та+ Те+ δТ,
где То – поле, создаваемое однородной намагниченностью земного шара, называемое дипольным; Тт – недипольное поле, называемое полем мировых магнитных аномалий; Та – поле локальных и региональных магнитных аномалий, обусловленных неоднородной намагниченностью верхних слоев земной коры; Те – поле, обусловленное внешними причинами; δТ – вариации магнитного поля во времени.
Сумма полей То+Тт образует главное поле, а сумму полей То+Тт+Те часто называют нормальным полем Земли. Такое подразделение во многом условно, но оно удобно для характеристики магнитного поля Земли. Сферический гармонический анализ геомагнитного поля, выполненный по современным и древним картам, свидетельствует о том, что с течением времени, начиная с 1840 г. по настоящее время эксцентричный диполь (магнитный центр) систематически смещался на северо-запад и удалялся от географического центра Земли. Величина магнитного момента Мо, начиная с 1829 г. по настоящее время систематически уменьшается примерно от 8,5*1022 до
8,0*1022 А*м2.
Эксцентричный диполь дрейфует в плоскости большого круга Земли, наклоненного к экватору под углом ~31°, со средней угловой скоростью порядка 0°,3 в год.
Представление об изменении магнитного момента диполя за предыдущие тысячелетия дают археомагнитные данные. Около двух тысяч лет тому назад магнитный момент Земли достигал максимальной величины, в полтора раза превышающей нынешнюю, а шесть тысяч лет тому назад был минимальным — около половины нынешнего. Таким образом, намечается период вариации магнитного момента Земли – 7–8 тыс. лет.
В процессе палеомагнитных исследований было открыто очень важное свойство древнего магнитного поля Земли – «инверсия».
Инверсия представляет собой смену направления магнитного момента (вектора напряженности магнитного поля) Земли на обратное. Известно, что перед инверсией напряженность магнитного поля уменьшается в среднем в
7–10 раз. Это сопровождается увеличением амплитуды его вековых вариаций, причем возмущенность поля достигает такого уровня, что происходят кратковременные изменения его полярности. Затем следует сама инверсия поля – обращение вектора напряженности 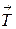 , а далее – постепенное увеличение напряженности поля до его первоначального абсолютного значения. Весь процесс
, а далее – постепенное увеличение напряженности поля до его первоначального абсолютного значения. Весь процесс
| <== предыдущая лекция | | | следующая лекция ==> |
| ПРИЛОЖЕНИЕ 1 | | | Эритроциты |
Дата добавления: 2015-06-10; просмотров: 1419;
