Электропроводность металлов.
Рассмотрим электронную структуру изолированного атома, использовав модель Бора: ядро и вращающиеся вокруг него по соответствующим орбитам электроны. Каждая такая орбита характеризуется определенным значением энергии. Энергетическая структура атомов может быть представлена различными энергетическими уровнями, заселенными определенным количеством электронов (рис.5.5, а). Расстояние между уровнями убывает по мере роста номера уровня (уровни не эквидистантны). Максимальное число электронов на уровне задано правилами квантования. На рис.5.5 это показано цифрами на уровнях Е1, Е2, и т.д.
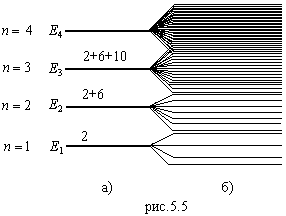 Энергетическая структура всех изолированных атомов одного элемента одинакова. Если взять N атомов, то уровни Е1, Е2, Е3… будут N‑кратно вырож-денными, т.е. будут одинаково повторены N раз.
Энергетическая структура всех изолированных атомов одного элемента одинакова. Если взять N атомов, то уровни Е1, Е2, Е3… будут N‑кратно вырож-денными, т.е. будут одинаково повторены N раз.
Сблизим N атомов так, чтобы они образовали кристалл. Расстояние между атомами в кристалле всегда несколько меньше, чем размер внешних оболочек атома, т.е. валентные электронные оболочки перекрываются. Это означает, что на уровне Ei должно находиться большее, чем раньше, число электронов. Однако это запрещено правилами квантования. Поэтому уровень расщепляется на N невырожденных энергетических уровней (рис.5.5), расстояние между которыми настолько мало, что переход с одного на другой почти не требует затрат энергии. В этом смысле распределение электронов по энергиям можно считать непрерывным. Совокупность уровней, на которые расщепился N-кратный уровень, называется энергетической зоной. Такие зоны показаны на рис.5.5, б.
Соседние зоны, разделенные интервалами энергий, называются запрещенными, так как в них нет разрешенных уровней энергии.
Итак, внутри кристалла внешние электроны:
а) коллективизированы, так как из-за перекрытия орбит они могут переходить от атома к атому;
б) могут занимать уровни внутри энергетической зоны;
в) число уровней внутри зоны определяется числом атомов в кристалле.
Теперь возникает вопрос: как распределяются электроны по уровням внутри зоны, какой статистике подчиняется это распределение.
Функция распределения частиц по энергиям согласно статистике Больцмана
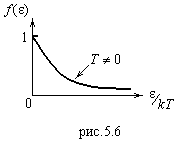
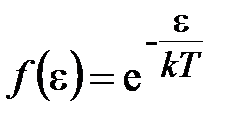
показана на рис.5.6.
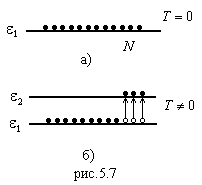
При 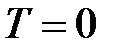 , согласно этой функции, должен быть занят лишь самый низкий уровень энергии (рис.5.7, а). Все N частиц должны быть на этом уровне. Но правила квантования запрещают это, потому что каждый уровень, согласно данным правилам, имеет лишь определенное количество мест. При повышении температуры часть частиц может занять и более высокие уровни энергии (рис.5.7, б). Из этого рассуждения ясно, что электроны не могут подчиняться статистике Больцмана.
, согласно этой функции, должен быть занят лишь самый низкий уровень энергии (рис.5.7, а). Все N частиц должны быть на этом уровне. Но правила квантования запрещают это, потому что каждый уровень, согласно данным правилам, имеет лишь определенное количество мест. При повышении температуры часть частиц может занять и более высокие уровни энергии (рис.5.7, б). Из этого рассуждения ясно, что электроны не могут подчиняться статистике Больцмана.
 Газ коллективизированных электронов – квантовый газ, подчиняющийся статистике Ферми-Дирака. Основные положения этой статистики рассмотрим без вывода.
Газ коллективизированных электронов – квантовый газ, подчиняющийся статистике Ферми-Дирака. Основные положения этой статистики рассмотрим без вывода.
1. Распределение электронов по энергиям следует функции.
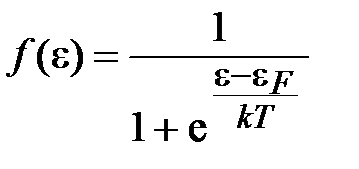 , (5.23)
, (5.23)
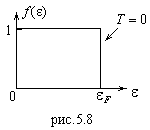 где
где 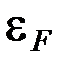 - энергия Ферми. Эта функция при
- энергия Ферми. Эта функция при 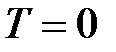 показана на рис.5.8, так как:
показана на рис.5.8, так как:
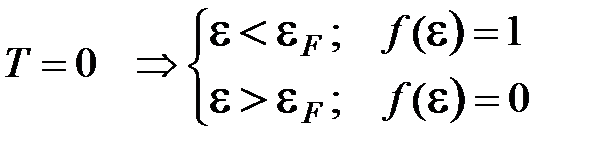 .
.
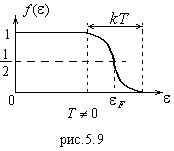 Энергия Ферми – самый высокий энергетический уровень, занятый электронами при
Энергия Ферми – самый высокий энергетический уровень, занятый электронами при 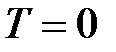 . Все уровни энергии выше
. Все уровни энергии выше 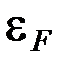 полностью свободны. Все уровни энергии ниже
полностью свободны. Все уровни энергии ниже 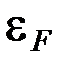 полностью заняты. Если
полностью заняты. Если 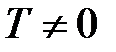 , то функция (5.23) имеет вид, представленный на рис.5.9, так как:
, то функция (5.23) имеет вид, представленный на рис.5.9, так как:
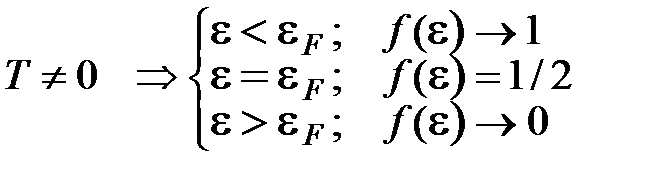
Ясно, что зона “размытия” распределения существует, поскольку энергии 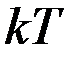 достаточно, чтобы перебросить электроны на свободные энергетические уровни, т.е. по ширине она
достаточно, чтобы перебросить электроны на свободные энергетические уровни, т.е. по ширине она 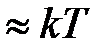 .
.
2. Величина энергии Ферми может быть рассчитана.
Введем фазовое пространство электрона – шестимерное пространство с координатными осями, на которых откладываются пространственные координаты 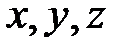 и соответствующие проекции импульса электрона
и соответствующие проекции импульса электрона 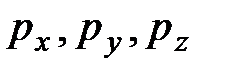 . Кинетическая энергия электрона:
. Кинетическая энергия электрона:
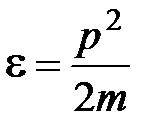 .
.
Импульс электрона:
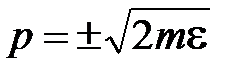 . (5.24)
. (5.24)
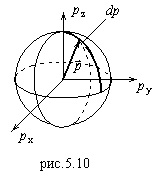
В фазовом пространстве точки, отвечающие значениям 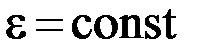 должны помещаться на сфере радиуса (5.24) (рис.5.10). В интервале энергий
должны помещаться на сфере радиуса (5.24) (рис.5.10). В интервале энергий 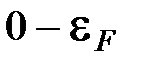 должны при
должны при 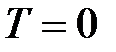 разместиться все N электронов. Рассчитаем число мест для электронов в фазовом пространстве в интервале импульсов
разместиться все N электронов. Рассчитаем число мест для электронов в фазовом пространстве в интервале импульсов 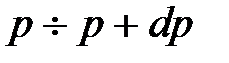 . Это объем сферического слоя ширины
. Это объем сферического слоя ширины 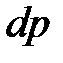 , деленный на объем одной элементарной ячейки в фазовом пространстве и умноженный на 2.
, деленный на объем одной элементарной ячейки в фазовом пространстве и умноженный на 2.
 .
.
Здесь учтено, что в одной фазовой ячейке объема 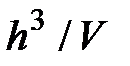 располагаются 2 электрона. Тогда общее число мест, занятых электронами:
располагаются 2 электрона. Тогда общее число мест, занятых электронами:
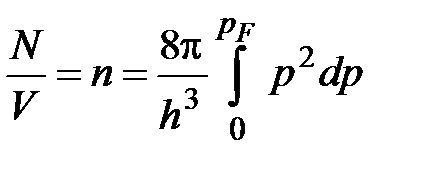 ,
,
где 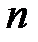 - концентрация электронов в единице объема. Отсюда:
- концентрация электронов в единице объема. Отсюда:
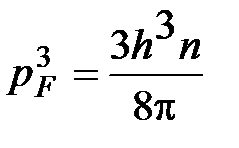 . (5.25)
. (5.25)
Таким образом, величина энергии Ферми равна:
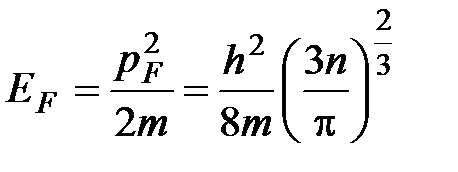 . (5.26)
. (5.26)
Для того чтобы оценить величину 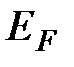 , рассчитаем так называемую температуру Ферми:
, рассчитаем так называемую температуру Ферми: 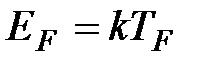 и приведем ее значения в таблице для ряда металлов. Здесь
и приведем ее значения в таблице для ряда металлов. Здесь 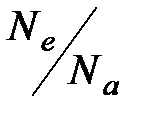 - число электронов на атом,
- число электронов на атом, 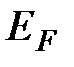 - энергия Ферми,
- энергия Ферми, 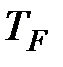 - температура Ферми.
- температура Ферми.
| Вещество | 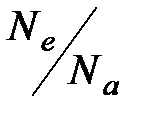
| 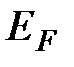 , эВ , эВ
| 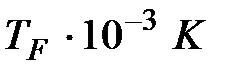
|
| Li | 4.7 | ||
| Na | 3.1 | ||
| Cu | 7.0 | ||
| Ag | 5.5 | ||
| Au | 5.5 |
Расчет проведен для следующих значений:
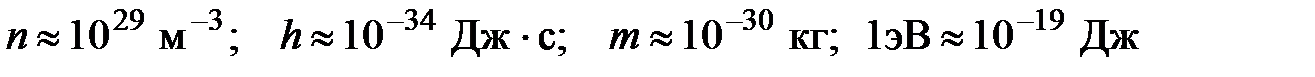 .
.
Видно, что 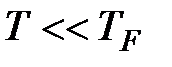 , поэтому зона “размытия” распределения Ферми (рис.5.9)
, поэтому зона “размытия” распределения Ферми (рис.5.9) 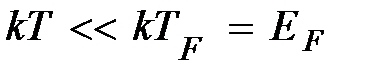 . Практически все электроны в металлах находятся на полностью занятых уровнях энергии. Из графика рис.5.9 видно, что лишь в зоне “размытия” и выше по энергиям есть свободные уровни, остальные электроны не могут изменить своей энергии, т.е. не могут участвовать в процессах теплопереноса. Число термически активированных электронов
. Практически все электроны в металлах находятся на полностью занятых уровнях энергии. Из графика рис.5.9 видно, что лишь в зоне “размытия” и выше по энергиям есть свободные уровни, остальные электроны не могут изменить своей энергии, т.е. не могут участвовать в процессах теплопереноса. Число термически активированных электронов 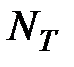 :
:
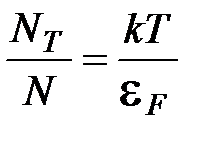 ;
; 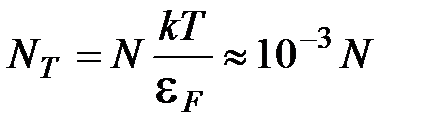 (5.27).
(5.27).
Ранее была выведена формула Друде (5.8) для электропроводности, которая теперь может быть записана в ином виде:
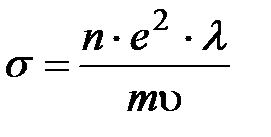 ,
,
 где время релаксации заменено выражением
где время релаксации заменено выражением 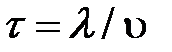 ; здесь
; здесь 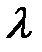 - длина свободного пробега;
- длина свободного пробега; 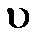 - скорость. В силу вышесказанного
- скорость. В силу вышесказанного 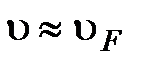 ; так как средняя кинетическая энергия электрона
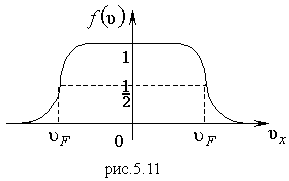
; так как средняя кинетическая энергия электрона 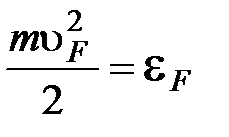 . На рис.5.11 представлена зависимость функции распределения
. На рис.5.11 представлена зависимость функции распределения 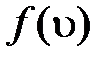 по скоростям от скорости
по скоростям от скорости 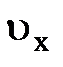 . Из рис. видно, что возможны два знака
. Из рис. видно, что возможны два знака 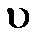 при одном и том же значении энергии. При этом число электронов
при одном и том же значении энергии. При этом число электронов 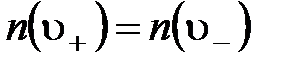 .
.
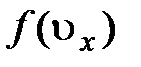
|
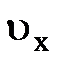
|
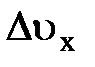
|
| рис. 5.12 |
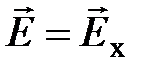 . Электрон приобретает добавочную скорость:
. Электрон приобретает добавочную скорость:
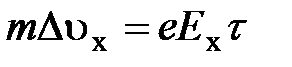 ;
;
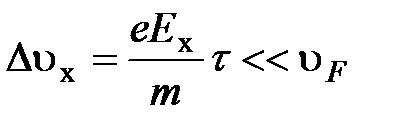 .
.
Оценка дает значение:
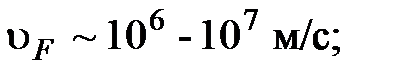
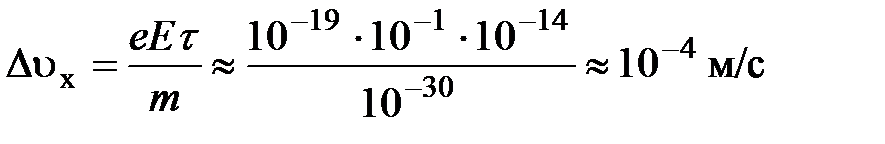 при
при 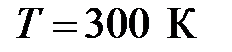 .
.
Распределение 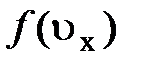 сместится в сторону
сместится в сторону 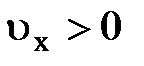 на
на 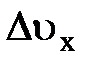 (рис.5.12). Электроны в заштрихованной области при
(рис.5.12). Электроны в заштрихованной области при 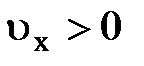 , имея большую энергию, будут стремиться занять места с меньшей энергией в заштрихованной области с
, имея большую энергию, будут стремиться занять места с меньшей энергией в заштрихованной области с 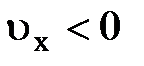 . Появится ток, при этом электроны будут двигаться в направлении, противоположном приложенному полю. Скорость движения электронов определяется их энергией, а она
. Появится ток, при этом электроны будут двигаться в направлении, противоположном приложенному полю. Скорость движения электронов определяется их энергией, а она 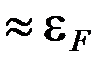 , т.е.
, т.е. 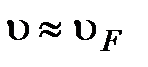 . Видно, что в формуле Друде
. Видно, что в формуле Друде 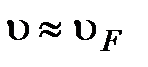 и
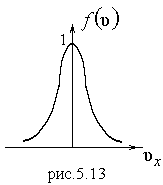
и 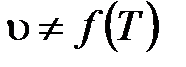 . На рис.5.13 и 5.14 показаны соответствующие рис.5.11 и 5.12 функции распределения для статистики Больцмана. Видно, что в этом случае все электроны изменяют свою энергия при приложении электрического поля.
. На рис.5.13 и 5.14 показаны соответствующие рис.5.11 и 5.12 функции распределения для статистики Больцмана. Видно, что в этом случае все электроны изменяют свою энергия при приложении электрического поля.
4. Как зависит 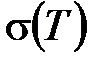 , если принять за основу формулу Друде?
, если принять за основу формулу Друде?
В формуле зависит от температуры лишь одна характеристика 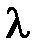 – длина свободного пробега. Экспериментально для меди получены следующие значения
– длина свободного пробега. Экспериментально для меди получены следующие значения 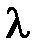 при температурах 300 К и 4 К:
при температурах 300 К и 4 К:
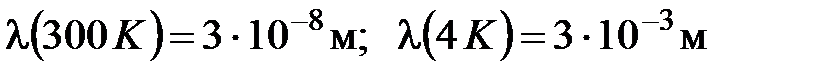 .
.
Видно, что с уменьшением температуры длина свободного пробега увеличивается. Физический смысл такой зависимости предельно прозрачен – уменьшение вероятности столкновения электрона с колеблющимися атомами решетки. Функционально зависимость электропроводности от температуры такова:
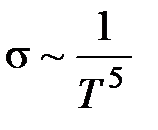 при низких температурах:
при низких температурах: 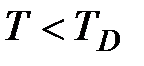 ;
;
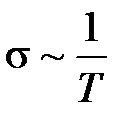 при высоких температурах:
при высоких температурах: 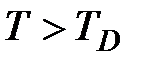 .
.
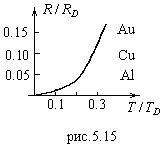

На рис.5.15 приведена зависимость относительного сопротивления меди, алюминия и золота от относительной температуры ( 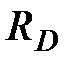 - сопротивление при температуре Дебая,
- сопротивление при температуре Дебая, 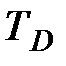 - температура Дебая).
- температура Дебая).
Дата добавления: 2015-06-01; просмотров: 993;
