Краткие сведения по квантовой механике

Теоретическим фундаментом электроники являются современные представления о природе и механизмах излучения, поглощения и распространение света, физической сущности электричества, строения атомов и молекул.

Некоторые из физических явлений можно объяснить с помощью классической физики, в которой электрону приписывают только корпускулярные свойства, а свет представляют в виде потока электромагнитных волн. В целом ряде случаев описание физического явления возможно лишь на основе квантовомеханической теории. Это, в частности, относится и к электронным процессам в проводниках и полупроводниках, лежащих в основе современных электронных приборов.

Зарождение квантовой механики совпало с началом XX века, когда классические представления о природе материи пришли в противоречие с целом рядом экспериментально наблюдаемых явлений:

1. тепловое излучение, в частности изучение абсолютно черного тела.

Из закона Релея-Джинса следует

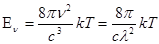, (1)

где ν – частота излучения;

λ = с/ ν – длина волны;

с – скорость света в вакууме;

k – постоянная Больцмана,

т.е. с увеличением частоты излучения, интенсивность излучения также должна увеличиваться, стремясь к бесконечности. Эксперимент же показывает, что по мере увеличения частоты интенсивность излучения увеличивается, достигает максимума, а затем спадает.

Данное принципиальное различие между теорией и экспериментом в области высокочастотного излучения получило в классической физике название «Ультрафиолетовой катастрофы».

2. Фотоэффект, эффект Комптона

Явление вырывание электронов из твердых и жидких веществ под действием света получило название внешнего фотоэффекта.

Эффект Комптона – упругое рассеяние электромагнитного излучения на свободных электронах, сопровождающееся увеличением длины волны. Наблюдается при рассеянии излучения малых длин волн – рентгеновского и гамма-излучения.

3. Устойчивость атома

Согласно законам электродинамики электрон, вращающийся вокруг ядра в его электрическое поле (движущийся с ускорением), должен излучать энергию в виде электромагнитных волн, терять скорость и в конце концов упасть на ядро. Получается, что стационарное состояние планетарной модели атома не возможна, т.е. атом должен быть неустойчив. Кроме того, частота обращения электрона вокруг ядра должна непрерывно меняться, а совокупность атомов должна давать сплошной спектр излучения, что противоречило действительности.

1. Первый шаг в направлении квантовой теории материи совершил Маркс Планк, который предложил в 1900 году гипотезу о том, что излучение и поглощение энергии материей происходит не непрерывно, а дискретно отдельными порциями – «квантами энергии» величиной

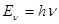, (2)

где h - постоянная Планка;

ν – частота.

2. Вскоре после этого (1907-1908) А. Эйнштейном была развита квантовая теория света, основывающаяся на представлении света в виде потока световых квантов – фотонов.

Согласно КВД каждой частице соответствует волна (или набор волн – волновой пакет), а каждой волне – эквивалентная частица. Например, тепловым колебаниям кристаллической решетки соотсветствуют фононы тепловых колебаний.

Каждый фотон, как и всякая частица, обладает энергией:

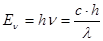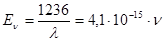, или , (3)

где h - постоянная Планка;

ν – частота;

с – скорость света;

λ – длина волны.

Помимо энергии фотон обладает также массой и импульсом.

Формула для массы фотона может быть непосредственно выведена из формулы, выражающей взаимосвязь массы и энергии в теории относительности:

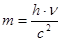. (4)

Масса фотона существенно отличается от массы микроскопических тел и масс других «элементарных» частиц. Это отличие состоит в том, что фотон не обладает массой покоя m₀. В самом деле, для фотона, движущегося в вакууме со скоростью света, применение формулы

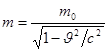, (5)

где m₀ – масса тела при скорости равной 0, т.е. масса покоя;

m – масса движущегося тела;

выражающей зависимость массы от скорости, приводит к абсурду (m= ∞), если считать, что у фотона существует отличная от нуля масса покоя. Таким образом, для фотона m₀=0, т.е. покоящихся фотонов не существует. Но тогда очевидно, что фотон всегда в любом веществе движется со скоростью равной скорости света, т.к. при другой скорости масса и энергия фотона были бы равны нулю, что не согласуется с формулой (4). Этот вывод не противоречит тому, что фазовая и групповая скорости света в веществе отличны от скорости света. Распространение света в среде сопровождается процессами «переизлучения» - фотоны поглощаются и вновь испускаются частицами среды.

Импульс фотона р_ф и его энергия Е_ν в соответствии с формулой теории относительности связаны соотношением

.

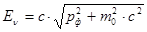Для фотона m₀=0 и

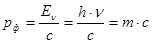. (6)

Если ввести волновое число 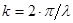(модуль вектора 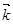, показывающего направление распространения волны в пространстве), то (6) можно переписать в виде

, (7)

где 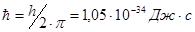- квант действия.

Направление импульса совпадает с направлением распространения света, характеризуемым волновым вектором 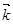, численно равным волновому числу

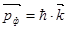. (8)

Т.о., фотон, подобно любой движущейся частице или телу, обладает энергией массой и импульсом. Все эти три корпускулярные характеристики фотона связаны с волновой характеристикой света – его частотой ν.

Одним из экспериментальных подтверждений наличия у фотонов импульса является существование светового давления. С квантовой точки зрения давление света на поверхность какого-либо тела обусловлено тем, что при соударении с этой поверхностью каждый фотон передает ей свой импульс.

Что очень важно, гипотеза Эйнштейна не отвергала волновую природу света, а лишь дополняла ее. Она свидетельствовала о сложной двойственной природе света. Свет одновременно обладает свойствами непрерывных электромагнитных волн и свойствами дискретных фотонов.

С уменьшением длины волны (увеличением частоты) все более отчетливо сказываются квантовые свойства света (красная граница фотоэффекта, фотохимические реакции). Вместе с тем волновые свойства коротковолнового излучения (например, рентгеновского) выражаются весьма слабо. Наоборот, у длинноволнового излучения квантовые свойства видны в малой степени и основную роль играют его волновые свойства. Именно поэтому большая группа оптических явлений (интерференция, дифракция, поляризация и др.) получает свое исчерпывающее объяснение в волновой оптике. Таким образом, если «перемещаться» по шкале электромагнитных волн слева направо, от длинных волн в сторону более коротких, то волновые свойства электромагнитного излучения будут постепенно уступать место квантовым свойствам.

Одновременное существование у света волновых и квантовых свойств, естественно, ставит вопрос об их сочетании и взаимозависимости.

Взаимосвязь между двойственными корпускулярно-волновыми свойствами находит простое истолкование при статическом подходе к рассмотрению вопроса о распространении света. В самом деле, все квантово-оптические явления убеждают нас в том, что свет – это поток дискретных частиц – фотонов, в которых локализованы энергия, импульс и масса излучения. Взаимодействие фотонов с веществом при прохождении света через какую-нибудь оптическую систему (например, дифракционную решетку) приводит к перераспределению фотонов в пространстве и возникновению дифракционной картины на экране, расположенном на пути света прошедшего сквозь систему.

Очевидно, что освещенность Е экрана в различных точках прямо пропорциональна суммарным энергиям фотонов попадающих в эти точки за единицу времени. Для монохроматического света Е = dn/dS, где dn/dS = n_о – число фотонов, попадающих на единичную площадку dS поверхности экрана за единицу времени. Величины n_о и Е пропорциональны вероятности попадания фотонов в рассматриваемую точку экрана.

С другой стороны, решение этой дифракционной задачи на основе волновых представлений о свойствах света показывает, что освещенность Е пропорциональна интенсивности I в данной точке экрана. Так как I~А² , где А – амплитуда световой волны, то Е~А².

Из сопоставления двух выражений для Е , полученных выше, можно сделать следующий вывод:

Квадрат амплитуды световой волны в какой-либо точке пространства является мерой вероятности попадания фотонов в эту точку.

Таким образом, корпускулярные и волновые свойства света не исключают, а, наоборот, взаимно дополняют друг друга. Они отражают две различные, но в тоже время тесно взаимосвязанные закономерности распределения электромагнитного излучения и его взаимодействие с веществом. Корпускулярные свойства обусловлены тем, что энергия, импульс и масса излучения локализованы в «частицах» – фотонах, волновые – статистическими закономерностями распределения фотонов в пространстве, т.е. закономерностями, определяющими вероятности нахождения фотонов в различных точках пространства.

3. Важнейшей вехой на пути к квантовой теории вещества стала теория Нильса Бора (1913г.) о строении атома водорода.

Принципиальным положением этой теории явилось утверждение о неприменимости классической электродинамики к движению электрона в атоме. Взяв гипотезу Планка о квантовой энергии и распространив ее на атомные системы, Бор сформулировал два постулата, явившихся основой его теории:

1. Постулат стационарных орбит (состояний) – существуют стационарные состояния атома, находясь в которых он не излучает энергию.

2. Постулат частот – при переходе атома из одного стационарного состояния в другое испускается или поглощается один фотон.

4. Наконец в 1924 г. Французский физик Луи де Бройль высказал гипотезу о том, что корпускулярно-волновая природа присуща не только электромагнитному излучению, но и отельным микрочастицам вещества – электронам, протонам, атомам и т.д. Это означает, что микрочастицы обладают не только корпускулярными свойствами, но и волновыми.

По де Бройлю свободная микрочастица, обладающая энергией Е и импульсом р , характеризуется также длиной волны

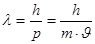(9)

и частотой

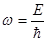или (10)

Вместо длины волны микрочастицу можно характеризовать волновым числом или вектором:

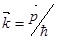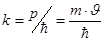; (11)

где m, 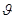– масса и скорость микрочастицы.

Волны, характерные для микрочастиц, параметры которых определяются уравнениями (9), (10) и (11), называются волнами де Бройля. Каждой микрочастице соответствует волна де Бройля (или набор волн), благодаря чему микрочастица в определенных условиях проявляет свои волновые свойства.

Гипотеза де Бройля подверглась многократной экспериментальной проверке. Ее неоспоримым подтверждением стали дифракционные картины, сфотографированные после пропускания пучков электронов через кристаллы, выполнявшие функцию дифракционных решеток.

Интересно отметить, что гипотеза де Бройля дала прекрасное физическое истолкование постулату стационарных орбит Бора. При движении электрона вокруг атомного ядра нельзя указать, в каком именно месте орбиты электрон находится. В этом случае его надо рассматривать не как частицу, а как волну, напоминающую туманное электронное облако, окружающее атомное ядро. На рис.2 схематически изображены электронные волны. Если после обхода по кругу голова волны не совпадает с ее хвостом, то горбы и впадины волны накладываются друг на друга, взаимно ослабляются и волна сама себе гаснет (рис.2,а). Условие стабильности волны состоит в том, что ее голова после обхода по кругу точно подгоняется к хвосту. Для этого необходимо, чтобы на окружности укладывалось целое число длин электронных волн (рис.2,б):

, n=1,2,…

где 2πr_n – длина орбиты.

Из этого уравнения можно найти радиусы орбит r_n, которые в точности совпадают с боровскими.

Гипотеза де Бройля и ее успешное экспериментальное подтверждение показали своеобразие таких материальных образований, какими являются микрочастицы. Совместно с теорией Эйнштейна он завершил развитие представлений о корпускулярно-волновом дуализме материи. Как у света, так и у микрочастиц вещества мы не можем одновременно наблюдать проявление сразу и корпускулярных и волновых свойств. В каждой конкретной ситуации микрообъект показывает только одно из своих свойств – либо корпускулярное, либо волновое. Если физический опыт поставлен так, что микрообъект ведет себя подобно волне, то его корпускулярная природа в таком опыте скрыта, не проявляется. И наоборот.

Своеобразие микрочастиц также в способе описания их поведения. Классическая ньютоновская механика для этого не подходит. Покажем это.

Классическая механика базируется на одном важнейшем постулате: существование жесткой причинно-следственной связи в поведении микрочастицы. Это означает, что в каждый момент времени микрочастица занимает строго определенное положение в пространстве, т.е имеет определенные координаты x, y, z. Одновременно частица обладает и строго определенным импульсом p = mv (его проекции р_x, р_y, р_z). Эта принципиальная возможность сколь угодно точного измерения координат и импульса микрочастицы одновременно считается ее неотъемлемым свойством. Координаты и импульс микрочастицы в каждый последующий момент времени однозначно связаны с соответствующими величинами в предыдущий момент времени и могут быть найдены с помощью классических уравнений движения.

Посмотрим, в какой мере указанный способ описания применим к микрочастице, обладающей волновыми свойствами.

Пусть микрочастица движется вдоль оси х и обладает импульсом р_х. Такой частице соответствует волна де Бройля λ=h/p_х. По свое сущности волна является объектом бесконечно протяженным в пространстве. Это означает, что невозможно для микрочастицы с импульсом p_х указать ее координату х.

Частица не может обладать одновременно и свойствами частицы и свойствами волны, т.к. мы не можем указать точное ее местоположение.

Может возникнуть подозрение, что в таком случае вообще невозможно указать местоположение микрочастицы в пространстве. Это не совсем так. Дело в том, что волновой объект не всегда «размазан» по всему пространству. Из теории колебаний известно, что если некоторое количество волн образуют, так называемый волновой пакет, то за счет взаимной интерференции эти волны гасят друг друга во всем пространстве за исключением некоторой ограниченной области тем меньше, чем шире диапазон Δλ значений длин волн, составляющий волной пакет.

Следовательно, если предположить, что волновые свойства микрочастицы отражает не одна волна де Бройля, а волновой пакет составленный из волн де Бройля, положение микрочастицы в пространстве можно локализовать в пределах некоторой ограниченной области. Правда при этом мы не сможем указать точное значение импульса микрочастицы, т.к. набору волн Δλ соответствует набор Δр_х значений импульса.

Если признавать наличие у микрочастицы волновых свойств, то нужно признать и принципиальную невозможность одновременного задания (измерения) ее координат и импульса. В тоже время можно одновременно указать некоторую область пространства с размерами Δx, Δy, Δz, в которых находится микрочастица и некоторый диапазон значений импульса Δр_х, Δр_y, Δр_z, которым она (микрочастица) обладает.

Связь между размерами пространственной области и диапазоном значений импульса была открыта Гейзенбергом в 1925г.

Δx · Δp_х ≥ h ; Δy · Δp_y ≥ h ; Δz · Δp_z ≥ h (12)

Δx · Δv_х ≥ h/m ; Δy · Δv_y ≥ h/m ; Δz · Δv_z ≥ h/m

Данные соотношения называют соотношениями неопределенностей Гейзенберга. Из этих соотношений следует, что чем точнее определяются координаты микрочастицы, тем неопределеннее становятся составляющие импульса и наоборот.

/Сказать, почему из за ошибки Гейзенберга не сделали атомную бомбу немцы./

Ясно, что отказ от основного постулата классической теории (механики) делает невозможным ее использование для описания поведения микрочастиц. Следовательно, ее необходимо заменить другой теорией, которая бы базировалась на вероятностном представлении о поведении микрочастиц. Такая теория была создана и получила название квантовой механики. В 1925г. Ее сформулировал 24 летний студент Гейзенберг, а в 1926г. Независимую формулировку дал австрийский физик Шредингер.