Смачивание неоднородных поверхностей.
Поверхность реальных твердых тел редко бывает однородной. На смачивание особенно сильное влияние оказывает наличие на твердой поверхности участков с различным поверхностным натяжением. В этом плане реальные поверхности можно классифицировать на две группы – поверхности, неоднородные по химическому составу отдельных участков, и поверхности с участками разной структуры. К первой группе можно, например, отнести поверхности композитных материалов, многофазных сплавов, пористых тел. Неоднородности второй группы обусловлены зависимостью поверхностного натяжения различных кристаллических граней от их ориентировки. Эти различия могут быть весьма велики, особенно для веществ, у которых кристаллическая решетка имеет сравнительно малую степень симметрии и поэтому анизотропия свойств кристалла проявляется особенно резко. Неоднородности структуры присущи поверхностям всех поликристаллических образований.
Влияние ориентировки кристаллических граней на смачивание обнаруживается, например, при контакте насыщенного раствора додециламина в четыреххлористом углероде (с добавкой октанола) с калиевыми квасцами: на грани (100) краевой угол острый, на грани (111) он близок к 90˚, а на грани (110) – тупой. При контакте капель циклогексана с полированными гранями монокристалла LiF краевой угол натекания на грани (100) был равен 45˚, на грани (111) – 26˚.
Влияние неоднородности твердой поверхности на смачивание сильно зависит от размера (масштаба) участков с различными поверхностными натяжениями. Если размеры неоднородных участков очень малы, примерно на порядок меньше предела чувствительности измерительного прибора (например, оптического микроскопа), то локальные искажения периметра смачивания не будут заметны. Периметр капли, сидящей на горизонтальной плоскости, будет практически правильной окружностью. Если же неоднородности велики (на 1 – 2 порядка больше предела разрешения прибора), то периметр смачивания будет представлять ломаную линию. В первом случае можно принять, что эффективное (среднее) значение поверхностного натяжения аддитивно складывается из натяжений участков различной природы с учетом занимаемой ими площади. Тогда можно рассчитать равновесный краевой угол θh при смачивании гетерогенной твердой поверхности, используя те же предположения, которые вводятся при выводе уравнения Юнга для однородной поверхности.
Пусть поверхность состоит из участков только двух типов (I и II). Поверхностные натяжения на границе с газом и жидкостью для поверхности I пусть будут 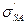 и
и 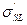 , а для типа II –
, а для типа II – 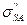 и
и 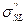 ; φi и φII - доли общей площади, занимаемые участками I и II (φi + φII = 1). В соответствии со сделанным допущением об аддитивности, используя уравнение Юнга, после несложных преобразований получим для расчета равновесных краевых углов на гетерогенной твердой поверхности, которая состоит из участков двух типов, причем размеры этих участков достаточно малы выражение:
; φi и φII - доли общей площади, занимаемые участками I и II (φi + φII = 1). В соответствии со сделанным допущением об аддитивности, используя уравнение Юнга, после несложных преобразований получим для расчета равновесных краевых углов на гетерогенной твердой поверхности, которая состоит из участков двух типов, причем размеры этих участков достаточно малы выражение:
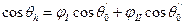 (2)
(2)
В общем случае, когда поверхность состоит из m участков различных типов (m > 2), уравнение (2) записывается в виде
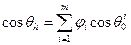 , причем
, причем 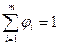 .
.
 Хорошее соответствие уравнения (2) с экспериментальными данными получено, например, при смачивании пластин из смеси линейного полиэтилена и полиметилметакрилата растворами метанола в воде и чистой водой (рис.3).
Хорошее соответствие уравнения (2) с экспериментальными данными получено, например, при смачивании пластин из смеси линейного полиэтилена и полиметилметакрилата растворами метанола в воде и чистой водой (рис.3).
| |
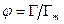 - доля поверхности раздела фаз твердое тело – жидкость, которая занята адсорбированными молекулами, тогда
- доля поверхности раздела фаз твердое тело – жидкость, которая занята адсорбированными молекулами, тогда 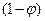 - доля исходной поверхности (Г – адсорбция, соответствующая концентрации раствора с; Гm – предельная адсорбция);
- доля исходной поверхности (Г – адсорбция, соответствующая концентрации раствора с; Гm – предельная адсорбция); 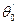 - краевой угол при смачивании поверхности, на которой имеется насыщенный монослой растворенного вещества (Г = Гm);
- краевой угол при смачивании поверхности, на которой имеется насыщенный монослой растворенного вещества (Г = Гm); 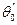 - краевой угол при смачивании поверхности чистым растворителем (Г = 0). Из уравнения Лэнгмюра
- краевой угол при смачивании поверхности чистым растворителем (Г = 0). Из уравнения Лэнгмюра 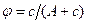 (А – коэффициент пропорциональный отношению скоростей десорбции и адсорбции). Примем, как и выше, что поверхностное натяжение
(А – коэффициент пропорциональный отношению скоростей десорбции и адсорбции). Примем, как и выше, что поверхностное натяжение 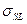 складывается аддитивно из натяжений участков φ и (1 – φ). Тогда получим:
складывается аддитивно из натяжений участков φ и (1 – φ). Тогда получим:
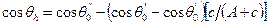 (3)
(3)
Это уравнение доступно для прямой проверки. В ряде случаев оно хорошо согласуется с экспериментальными результатами, например, при избирательном смачивании в системе кальцит – вода – растворы карбоновых кислот в бензоле. Отклонения имеет место в системах, в которых адсорбция на поверхности происходит не равномерно, а с образованием мозаичной структуры.
Если размеры неоднородных участков становятся порядка нескольких мкм и более, условия смачивания резко меняются. Основное отличие заключается в следующем.
Пусть твердая поверхность состоит из участков двух типов I и II и участок I смачивается лучше: 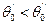 . Пусть в некоторый момент времени линия смачивания проходит через участок I и динамический краевой угол равен
. Пусть в некоторый момент времени линия смачивания проходит через участок I и динамический краевой угол равен 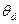 . При натекании переход линии смачивания на участок типа II приведет к увеличению свободной поверхностной энергии. Следовательно, граница участков I и II с разным поверхностным натяжением представляет энергетический барьер для перемещения линии смачивания по твердой поверхности. Напротив, переход линии смачивания на тот участок, который смачивается лучше, происходит самопроизвольно, без затраты внешней работы. Аналогично, можно показать, что при отекании энергетический барьер возникает при переходе линии смачивания с участка, на котором равновесный краевой угол больше.
. При натекании переход линии смачивания на участок типа II приведет к увеличению свободной поверхностной энергии. Следовательно, граница участков I и II с разным поверхностным натяжением представляет энергетический барьер для перемещения линии смачивания по твердой поверхности. Напротив, переход линии смачивания на тот участок, который смачивается лучше, происходит самопроизвольно, без затраты внешней работы. Аналогично, можно показать, что при отекании энергетический барьер возникает при переходе линии смачивания с участка, на котором равновесный краевой угол больше.
Таким образом, наличие достаточно больших неоднородных участков вызывает появление энергетических барьеров на границе между ними и как следствие появление состояний метастабильного равновесия. В результате статические краевые углы могут существенно отличаться от равновесного значения, определяемого уравнением (2). Поскольку положения метастабильного равновесия при натекании и отекании не совпадают, неоднородность твердой поверхности вызывает различие краевых углов натекания и отекания, т.е. она усиливает гистерезис смачивания.
Для расчета высоты энергетических (потенциальных) барьеров при переходе линией смачивания границы неоднородных участков Джонсоном Деттром была развита схема, которая во многих отношениях аналогична их же схеме, применяемой для расчета краевых углов натекания и отекания на шероховатой поверхности. Предполагалось, что горизонтально расположенная плоская поверхность состоит их участков двух типов. Эти участки расположены в виде узких концентрических колец равной ширины. Ширина колец достаточно велика, чтобы на границах участков возникали энергетические барьеры для перехода периметра смачивания Капля, размеры которой значительно больше ширины колец, помещается в общий центр колец. Основные выводы этой работы состоят в следующем.
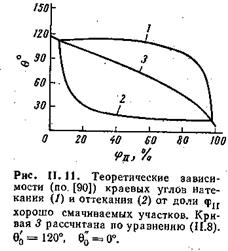 Из расчетов высоты энергетических барьеров следует, что при натекании состояния метастабильного равновесия возникают, когда периметр смачивания доходит до наружного края кольца из того материала, который смачивается лучше (где меньше равновесный краевой угол). При отекании периметр смачивания задерживается у внутренних сторон колец, которые смачиваются лучше. Наличие метастабильных состояний усиливает гистерезис смачивания. Потенциальные барьеры преодолеваются за счет колебаний жидкости, поэтому чем больше энергия капли в момент ее соприкосновения с подложкой, тем меньше соответствующее проявление гистерезиса краевых углов.
Из расчетов высоты энергетических барьеров следует, что при натекании состояния метастабильного равновесия возникают, когда периметр смачивания доходит до наружного края кольца из того материала, который смачивается лучше (где меньше равновесный краевой угол). При отекании периметр смачивания задерживается у внутренних сторон колец, которые смачиваются лучше. Наличие метастабильных состояний усиливает гистерезис смачивания. Потенциальные барьеры преодолеваются за счет колебаний жидкости, поэтому чем больше энергия капли в момент ее соприкосновения с подложкой, тем меньше соответствующее проявление гистерезиса краевых углов.
| |
| |
Соответственно угол натекания может быть достаточной характеристикой смачивания участков с малым поверхностным натяжением, а угол отекания – участков с большим поверхностным натяжением.
Дата добавления: 2015-04-05; просмотров: 1843;
