Друге начало термодинаміки для нестатичних процесів. Нерівність Клаузіуса.

Існують декілька еквівалентних формулювань другого початку термодинаміки:

· Постулат Клаузіуса : "Неможливий процес, єдиним результатом якого була б передача тепла від більш холодного тіла до більш гарячого" ^[1] (такий процес називається процесом Клаузіуса).

· Постулат Томсона (Кельвіна) : "Неможливий круговий процес, єдиним результатом якого було б виробництво роботи за рахунок охолодження теплового резервуара" (такий процес називаєтьсяпроцесом Томсона).

Еквівалентність цих формулювань легко показати. У самому справі, припустимо, що постулат Клаузіуса невірний, тобто існує процес, єдиним результатом якого була б передача тепла від більш холодного тіла до більш гарячого. Тоді візьмемо два тіла з різною температурою (нагрівач і холодильник) і проведемо кілька циклів теплової машини, забравши тепло 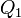у нагрівача, віддавши 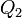холодильника і зробивши при цьому роботу 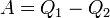. Після цього скористаємося процесом Клаузіуса і повернемо тепло 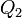від холодильника нагрівачу. У результаті виходить, що ми зробили роботу тільки за рахунок відбирання теплоти від нагрівача, тобто постулат Томсона теж невірний.

З іншого боку, припустимо, що є невірним постулат Томсона. Тоді можна відняти частину тепла у більш холодного тіла і перетворити в механічну роботу. Цю роботу можна перетворити в тепло, наприклад, за допомогою тертя, нагрів більш гаряче тіло. Значить, з невірності постулату Томсона слід невірність постулату Клаузіуса.

Таким чином, постулати Клаузіуса і Томсона еквівалентні.

Інша формулювання другого початку термодинаміки грунтується на понятті ентропії :

· "Ентропія ізольованої системи не може зменшуватися" ( закон неубиванія ентропії).

Таке формулювання грунтується на уявленні про ентропії як про функції стану системи, що також має бути постульовано.

Другий закон термодинаміки в аксіоматичної формулюванні Рудольфа Юліуса Клаузіуса (RJ Clausius, 1865) має наступний вигляд ^[2] :

Для будь квазиравновесной термодинамічної системи існує однозначна функція термодинамічного стану 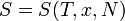, Звана ентропією, така, що її повний диференціал .

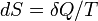У стані з максимальною ентропією макроскопічні незворотні процеси (а процес передачі тепла завжди є незворотнім через постулату Клаузіуса) неможливі. Нерівність Клаузіуса. Ентропія

Припустимо, що аналізованих тіло може обмінюватися теплотою лише з нескінченними тепловими резервуарами, внутрішня енергія яких настільки велика, що при розглянутому процесі температура кожного залишається строго постійною. Припустимо, що над тілом був здійснений довільний круговий процес, тобто по закінченні процесу воно знаходиться абсолютно в тому ж стані, що і на початку. 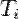Нехай при цьому за весь процес воно запозичило з i-го резервуару, що знаходиться при температурі , Кількість теплоти 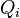. Тоді вірно наступне нерівність Клаузіуса:

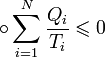
Тут 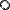позначає круговий процес. У загальному випадку теплообміну із середовищем змінної температури нерівність набуває вигляду

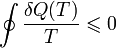
Тут 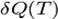- Кількість теплоти, передане ділянкою середовища з (постійної) температурою 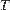. Це нерівність застосовне для будь-якого процесу, здійснюваного над тілом. В окремому випадку квазістатичного процесу воно переходить в рівність. Математично це означає, що для квазістатичних процесів можна ввести функцію стану, звану ентропією, для якої

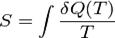
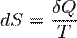тут 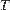- Це абсолютна температура зовнішнього теплового резервуара. У цьому сенсі 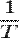є інтегруючим множником для кількості теплоти.

Для неквазістатіческіх процесів таке визначення ентропії не працює. Наприклад, при адіабатичному розширенні газу в порожнечу

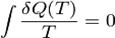однак ентропія при цьому зростає, в чому легко переконатися, перевівши систему в початковий стан квазістатичного і скориставшись нерівністю Клаузіуса. Крім того, ентропія (у зазначеному сенсі) не визначена для нерівноважних станів системи, хоча в багатьох випадках систему можна вважати локально рівноважної і володіє деяким розподілом ентропії.