Екситони. Екситони Ваньє-Мотта. Екситони Френкеля.

. Ексито́н (від лат. excito — збуджую) — квазічастинка, електронне збудження внапівпровіднику чи діелектрику, яке не переносить електричного заряду чимаси.

Фізична природа[ред. • ред. код]

За своєю природою екситон — зв'язаний стан електрона й дірки, що мігрує покристалу.

Хоча екситон складається з електрона та дірки, його треба розглядати як самостійну (не звідну) квазічастинку у випадках, коли енергія взаємодії електрона та дірки того ж порядку, що й енергія їхнього руху, а енергія взаємодії між двома екситонами мала в порівнянні з енергією кожного з них. Екситон можна вважати елементарною квазічастинкою в тих явищах, в яких він бере участь як єдина стійка система, що не зазнає на собі дій сторонніх чинників, які могли б його зруйнувати.

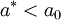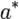Екситон може бути представлений як зв'язаний стан електрона провідності та дірки, розташованих або в одному вузлі кристалічної ґратки (екситон Френкеля, , де — радіус екситона, 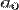— період ґратки), або на відстанях, значно більших за міжатомні (екситон Ваньє-Мотта, ).

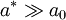В напівпровідниках, за рахунок великої діелектричної проникності існують тільки екситони Ваньє-Мотта, які утворюють воднеподібні серії рівнів. Екситони Френкеля застосовні перш за все до молекулярних кристалів.

Спіновий стан екситонів[ред. • ред. код]

Обидві квазічастинки, які входять до складу екситона: електрон і дірка, є ферміонами, тобто мають напівцілий спін. Згідно з правилами додавання спінів сумарний спін екситона цілий, тобто екситон є бозоном. Екситони із рівним нулю сумарним спіном називаються синглетними. Екситони із сумарним спіном, який дорівнює одиниці, називаються триплетними. При випадковій зустрічі двох квазічастинок із напівцілим спіном імовірність утворення синглетного екситона дорівнює 1/4, трипленого — 3/4. Зазвичай триплетні екситони мають набагато більший час життя, ніж синглетні екситони, оскільки переходи з триплетних станів у синглетний основний стан кристалу заборонені правилами відбору.

Екситони в аморфних матеріалах[ред. • ред. код]

Поняття екситона застосовується також для опису безструмових збуджень у речовинах, які не мають трансляційної симетрії. Такий екситон залишається зв'язаним станом електрона й дірки, але характеризується хвильовим векторомі втрачає властивість когерентності. Переміщення таких збуджених станів речовини відбувається стрибками. Серед невпорядкованих систем, у яких існують екситонні збудження, особливе місце займають органічні аморфні напівпровідники й спряжені полімери.

Екситон Френкеля або екситон малого радіуса — електронне збудження в кристалі, що не переноситьелектричного струму, граничний випадок екситона. Електрон та дірка, що складають екситон Френкеля, належать одному вузлу або сусіднім вузлам кристаличної ґратки, таким чином, радіус екситона становить величину того ж порядку, що й період ґратки.

Екситони Френкеля характерні для молекулярних кристалів, органічні молекули яких слабо взаємодіють між собою восновному стані й доволі сильно в збудженому. Цим забезпечується можливість вільної міграції збудження від однієї молекули до іншої.

Екситонами Френкеля є також збудження кріокристалів.

Зазвичай екситони Френкеля формують вузьку екситонну зону й мають доволі значну ефективну масу.

Названий на честь радянського фізика Якова Ілліча Френкеля.

Теорія[ред. • ред. код]

Нехай молекули в кристалі розташовані періодично, і кожну з них можна описати як дворівневу систему з основним і збудженим станом, хвильові функції яких 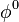та 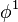, відповідно. Гамільтоніан кристалу має вигляд

,

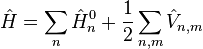де 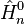- гамільтоніан окремої молекули, розташованої в n-му вузлі ґратки.

Хвильову функцію системи шукають у вигляді

.

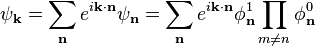Енергія такого збудження дорівнює

,

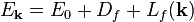де 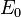- енергія збудження ізольованої молекули,

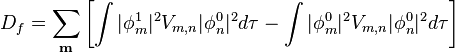
є енергією взаємодії збудженої молекули з незбудженими сусідами, а

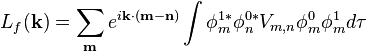
є матричним елементом переносу збудження з m-тої молекули на n-ту.

Завдяки періодичності кристалу вказані суми не залежать від n, а тому 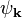є розв'язком задачі. 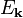задає неперервний спектр збудженнь.

Екситон Ваньє-Мотта — екситон, радіус якого значно більший за характерний період ґратки (на відміну від екситонів Френкеля).

Екситони Ваньє-Мотта існують в напівпровідниках за рахунок великої діелектричної проникності останніх. Велика діелектрична проникність призводить до послаблення кулонівської взаємодії між електроном і діркою, що й є причиною великого радіусу екситона.

Сам термін екситон був запропонований Френкелем в 1931 році. Френкель сформолював ідею існування таких квазічастинок. Уявлення про екситон великого радіусу, як про один з граничних випадів екситона взагалі, базується на теоретичній роботі Ваньє, але остаточно воно було сформульоване в роботах Мотта. Тому така квазічастинка отримала назву екситона Ваньє-Мотта.

Енергетичний спектр екситона[ред. • ред. код]

Тривимірний випадок[ред. • ред. код]

Для розрахунку енергетичного спектру екситона Ваньє-Мотта скористаємось примітивною моделлю. Будемо вважати ефективні маси електрона та дірки ізотропними. Також вважаємо, що відстань між електроном та діркою велика, в цьому випадку можна користуватися методом ефективної маси. Тоді рівняння Шредінгера для такої системи матиме вигляд:

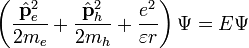
За допомогою заміни змінних відокремлюють поступальний рух центру мас та обертальний рух частинок навколо центру мас, що приводить до рівняння:

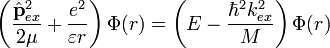
Це рівняння аналогічне рівнянню Шредінгера для атома водню. Звідси витікає, що дисперсійна залежність енергії екситона має вигляд:

,

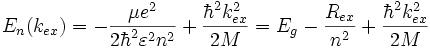де M = me+mh, 1/μ = 1/me+1/mh — зведена маса, r = re — rh.

Величина Rex = μe4/2ħ2с2 за аналогією зі сталою Рідберга для атома водню назвається екситонним Рідбергом.

Таким чином, для екситона у стані спокою, ми отримуємо набір дискретних водневих рівнів, які відповідають енергіям збудження, меншим за Eg (ширина забороненої зони). Для енергій E > Eg + ħ2k2ex/2M розв'язки належатьнеперервному спектру, що вказує на незалежний рух електрона та дірки.