Адиабатический процесс. Политропный процесс.

Адиабатическим называется процесс, при котором отсутствует теплообмен (dQ=0) между системой и окружающей средой. К адиабатическим процессам можно отнести все быстро протекающие процессы. Например, адиабатическим процессом можно считать процесс в двигателях внутреннего сгорания(расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т.д.

Из первого начала термодинамики (dQ=dU+dA) для адиабатического процесса следует, что

dА=-dU, (2.6.1)
т.е. внешняя работа совершается за счет изменения внутренней энергии системы.

Используя выражение для произвольной массы газа перепишем уравнение в виде

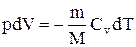. (2.6.2)

Продифференцировав уравнение состояния для идеального газа 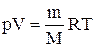, получим

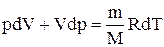. (2.6.3)
Исключим из (2.6.2) и (2.6.3) температуру Т:

.
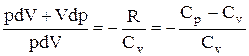Разделив переменные и учитывая, что 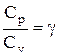найдем

.

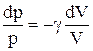Интегрируя это уравнение в пределах от p₁ до р₂ и соответственно от V₁ до V₂, а затем потенцируя, придем к выражению

.

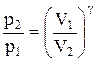или

.

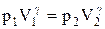Так как состояния 1 и 2 выбраны произвольно, то можно записать

PV^g=const. (2.6.4)
Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.

Для перехода к переменным Т, V или р, Т исключим из (2.6.4) с помощью уравнения Клапейрона-Менделеева:

,

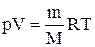соответственно давление или объем:

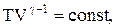(2.6.5)

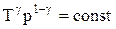. (2.6.6)

Эти выражения представляют собой уравнения адиабатического процесса. В этих уравнениях безразмерная величина

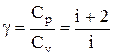(2.6.7)
называется показателем адиабаты (или коэффициентом Пуассона). Для одноатомных газов (Ne, He и др.), достаточно хорошо удовлетворяющих условию идеальности, i=3, g =1,67. Для двухатомных газов (Н₂, N₂, О₂ и др.) i=5, g =1,4. Значения вычисленные по формуле (2.6.7), хорошо подтверждаются экспериментом.

Диаграмма адиабатического процесса (адиабат а) в координатах р, V изображается гиперболой (рис. 2.6.1).

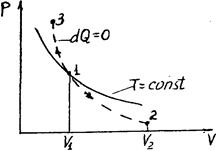Рис. 2.6.1

На рисунке видно, что адиабата ( 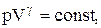) более крута, чем изотерма (pV=const). Это объясняется тем, что при адиабатическом сжатии 1-3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.

Вычислим работу, совершаемую газом в адиабатическом процессе.
Запишем уравнение в виде

.

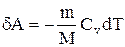Если газ адиабатически расширяется от объема V₁ до V₂, то его температура уменьшается от T₁ до Т₂ и работа расширения идеального газа

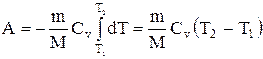. (2.6.8)

Применяя те же приемы, выражение (2.6.8) для работы при адиабатическом расширении можно преобразовать к виду

.

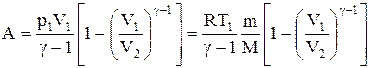Работа, совершаемая газом при адиабатическом расширении 1-2 (определяется заштрихованной площадью, выполненной на рис. 61), меньше, чем при изотермическом. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом - температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты.

Рассмотренные изохорный, изобарный, изотермический и адиабатический процессы имеют общую особенность - они происходят при постоянной теплоемкости. В первых двух процессах теплоемкости соответственно равны С_v и С_p, в изотермическом процессе (dT=0) теплоемкость равна ±¥, в адиабатическом (dQ=0) теплоемкость равна нулю. Процесс, в котором теплоемкость остается постоянной, называется политропным.

Исходя из первого начала термодинамики при условии постоянства теплоемкости (C=const), можно вывести уравнение политропы:

pVⁿ=const, (2.6.9)
где 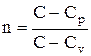- показатель политропы. Очевидно, что при С=0, n=gполучается уравнение адиабаты; при С=¥, n=l - уравнение изотермы; при С=С_p, n=0 - уравнение изобары, при С=С_v , n=±¥ - уравнение изохоры. Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.

2.7 Круговой процесс (цикл).
Обратимые и необратимые процессы.

Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное. На диаграмме процессов цикл изображается замкнутой кривой (рис. 2.7.1).

Цикл, совершаемый идеальным газом, можно разбить на процессы расширения (1-2) и сжатия (2-1) газа. Работа расширения (определяется площадью фигуры 1а2V₂V₁) положительна (dV > 0), работа сжатия (определяется площадью фигуры 2blV₁V₂2) отрицательна (dV < 0). Следовательно, работа, совершаемая газом за цикл, определяется площадью, охватываемой замкнутой кривой. Если за цикл совершается положительная работа 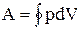>0 (цикл протекает по часовой стрелке), то он называется прямым (рис. 2.7.1,а), если за цикл совершается отрицательная работа 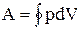<0 (цикл протекает против часовой стрелки), то он называется обратным (рис. 2.7.1,6).

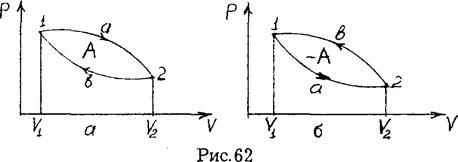
Прямой цикл используется в тепловых двигателях – периодически действующих двигателях, совершающих работу за счет полученной извне теплоты. Обратный цикл используется в холодильных машинах - периодически действующих установках, в которых за счет работы внешних сил теплота переносится к телу с более высокой температурой.

В результате кругового процесса система возвращается в исходное состояние и, следовательно, полное изменение внутренней энергии газа равно нулю.

Работа совершаемая за цикл, равна количеству полученной извне теплоты. Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому

Q=Q₁-Q₂,

гдеQ₁ - количество теплоты, полученное системой, Q₂ - количество теплоты, отданное системой. Поэтому термический коэффициент полезного действия для кругового процесcа

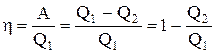. (2.7.1)

Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении, причем если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым.

Любой равновесный процесс является обратимым. Обратимые процессы- это идеализация реальных процессов. Их рассмотрение важно по двум причинам: многие процессы в природе и технике практически обратимы; обратимые процессы являются наиболее экономичными; имеют максимальный термический коэффициент полезного действия, что позволяет указать пути повышения кпд реальных тепловых двигателей.

2.8 Энтропия. Ее статистическое толкование
и связь с термодинамической вероятностью.

Понятие энтропии введено в 1865 г. Р.Клаузиусом. Для выяснения физического содержания этого понятия рассматривают отношение теплоты Q, полученной телом в изотермическом процессе, к температуре Т теплоотдающего тела, называемое приведенным количеством теплоты.

Приведенное количество теплоты, сообщаемое телу на бесконечно малом участке процесса, равно 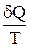. Строгий теоретический анализ показывает, что приведенное количество теплоты, сообщаемое телу в любом обратимом круговом процессе, равно нулю:

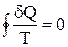. (2.8.1)

Из равенства нулю интеграла (2.8.1), взятого по замкнутому контуру следует, что подынтегральное выражение 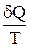есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние. Таким образом,

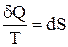. (2.8.2)

Функция состояния, дифференциалом которой является 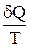, называется энтропией и обозначается S.

Из формулы (2.7.2) следует, что для обратимых процессов изменение
энтропии

DS=0. (2.8.3)

В термодинамике доказывается, что энтропия системы, совершающей необратимый цикл, возрастает:

DS>0. (2.8.4)

Выражения (2.8.3) и (2.8.4) относятся только к замкнутым системам, если же система обменивается теплотой с внешней средой, то ее энтропия может вести себя любым образом. Соотношения (2.8.3) и (2.8.4) можно представить в виде неравенства Клаузиуса

DS 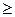0, (2.8.5)

т.е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).

Если система совершает равновесный переход из состояния 1 в состояние 2, то, согласно (2.8.2), изменение энтропии

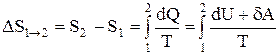, (2.8.6)
где подынтегральное выражение и пределы интегрирования надо выразить через величины, характеризующие исследуемый процесс. Формула (2.8.6) определяет энтропию лишь с точностью до аддитивной постоянной.

Физический смысл имеет не сама энтропия, а разность энтропии.

Исходя из выражения (2.8.6), найдем изменение энтропии в процессах идеального газа. Так как

,

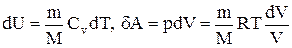то ,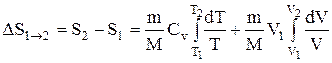

или 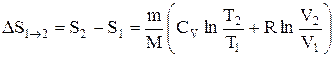, (2.8.7)

т.е. изменение энтропии 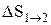идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида процесса перехода 1®2.

Так как для адиабатического процесса dQ=0, то DS=0 и, следовательно, S=const, т.е. адиабатический обратимый процесс протекает при постоянной энтропии. Из формулы (2.8.7) следует, что при изотермическом процессе (T₁=T₂)

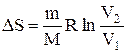
при изохорном процессе (V₁ =V₂)

.

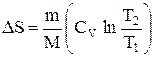Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропии тел, входящих в систему.

Более глубокий смысл энтропии вскрывается в статистической физике, энтропия связывается с термодинамической вероятностью состояния системы. Термодинамическая вероятность W состояния системы - это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние.

Согласно Больцману, энтропия S системы и термодинамическая вероятность связаны между собой следующим образом:

S=kInW, (2.8.8)
где k - постоянная Больцмана. Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Формула Больцмана позволяет дать энтропии следующее статистическое толкование: энтропия является мерой неупорядоченности системы. В самом деле, чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия. В состоянии равновесия - наиболее вероятного состояния системы - число микросостояний максимально, при этом максимальна и энтропия.
Так как реальные процессы необратимы, то можно утверждать, что все
процессы в замкнутой системе ведут к увеличению ее энтропии - принцип возрастания энтропии. При статистическом толковании энтропии это означает, что процессы в замкнутой системе идут в направлении увеличения числа микросостояний, иными словами, от менее вероятных к более вероятным.

Сопоставляя выражения (2.8.5) и (2.8.8), видим, что энтропия и термодинамическая вероятность состояний замкнутой системы могут либо возрастать (в случае необратимых процессов), либо оставаться постоянными (в случае обратимых процессов).

Отметим, однако, что эти утверждения имеют место для систем, состоящих из очень большого числа частиц, но могут нарушаться в системах с малым числом частиц. Для "малых" систем могут наблюдаться флуктуации, т.е. энтропия и термодинамическая вероятность состояний замкнутой системы на определенном отрезке времени могут убывать, а не возрастать, или оставаться постоянными.