Потенциалов
| Потребители Поставщики | В1= 150 | В2= 230 | В3= 160 | В4= 60 | Ui | ||||
| А1= 170 | |||||||||
| А2= 250 | - 1 | ||||||||
| А3= 180 | |||||||||
| Vj |
Шаг З. Проверка первоначального плана на оптимальность
Проверка плана на оптимальность исходит из принципа, что при любом его изменении, т.е. при перестановке перевозок в свободные квадраты, условная цена в пунктах потребления не должна стать меньше, чем в принятом нами плане. Следовательно, для свободных квадратов должно быть выполнено условие
Ui + Cij ≥ Vj . (2.5)
Осуществляем проверку:
для квадрата 1.1 Ui + Cij = 0 + 3 = 3 < 5;
1.2 Ui + Cij = 0 + 5 = 5 > 3;
1.3 Ui + Cij = -1 + 6 = 5 = 5;
1.4 Ui + Cij = -1 + 5 = 4 >2;
1.5 Ui + Cij = 0 + 4 = 4 > 3;
1.6 Ui + Cij = 0 + 5 = 5 > 2.
Проверка показывает, что условие оптимальности не выполняется лишь для квадрата 1.1, и если бы мы отправляли продукт от первого поставщика первому потребителю, то его стоимость в первом пункте потребления была бы ниже, чем в первоначальном плане.
Квадраты, в которых условие оптимальности (2.5) не выполняется, отмечаются знаками плюс.
Шаг 4. Оптимизация плана перевозок
Для оптимизации плана необходимо переместить перевозку в квадрат 1.1. Перемещение производится таким образом, чтобы по отношению к выбранному квадрату образовать связку. Для этого необходимо провести замкнутую ломаную линию, состоящую из горизонтальных и вертикальных линий (по принципу хода ладьи в шахматах), в которой одной из вершин полученного многоугольника является свободный квадрат, не отвечающий условию оптимальности, а остальные вершины должны находиться в занятых квадратах.
После образования связки свободному квадрату и связанным с ним занятым квадратам присваиваем поочередно знаки плюс и минус, начиная со свободного квадрата. Из квадратов со знаком минус перемещаем перевозки в квадраты со знаком плюс. Чтобы не получить отрицательных перевозок, перемещаем наименьшее количество перевозок, которое находится в квадратах связки со знаком минус.
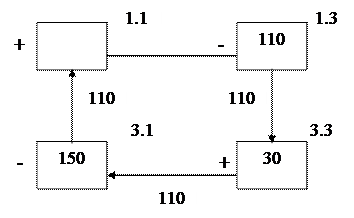
В нашем примере связка образуется из свободного квадрата 1.1, в который необходимо переместить перевозку из занятых квадратов 1.3, 3.3, 3.1. Присваиваем квадрату 1.1 знак плюс, квадрату 1.3 – знак минус, квадрату 3.3 – знак плюс и квадрату 3.1 – знак минус. Полученная связка представлена на рис. 2.1. Наименьшая перевозка со знаком минус находится в квадрате 1.3. Она равна 110 единицам. Это количество и перемещаем. В результате в квадрате 1.1 перевозка будет равна 110 единицам, в квадрате 3.1 – 40 единицам, в квадрате 3.3 – 140 единицам, а квадрат 1.3 станет свободным (рис. 2.2).
 | |||||||||
 | 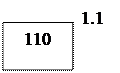 | ||||||||
| |||||||||
 | |||||||||
| | |||||||||
Рис.2.1 Рис. 2.2
Необходимо иметь в виду, что если план не является оптимальным одновременно для нескольких квадратов, в первую очередь производится перемещение перевозок в тот квадрат, в котором условие оптимальности нарушено больше, чем во всех остальных, т.е. в котором разность Vj - (Ui +Cij) максимальная.
Законченный цикл вычислений, приводящий к получению нового варианта прикрепления потребителей к поставщикам, называется итерацией.
Для нового плана вычисляем новые значения потенциалов и проверяем новый вариант на оптимальность, т. е. повторяем шаги 2 и 3.
Все расчеты нового плана прикрепления, потребителей к поставщикам приведены в табл. 2.5.
Из данных, приведенных в табл. 2.5, видно, что новый план прикрепления потребителей к поставщикам является оптимальным.
Таблица 2.5
Дата добавления: 2015-05-19; просмотров: 1053;
