Продолжительность жизни вида

Продолжительность жизни вида зависит от условий (факторов) жизни. Различают физиологическую и максимальную продолжительность жизни.

Физиологическая продолжительность жизниопределяется только физиологическими возможностями организма. Теоретически она возможна, если допустить, что в период всей жизни организма на него не оказывают влияние лимитирующие факторы.

До максимальной продолжительности жизни может дожить лишь малая доля особей в реальных условиях среды. Эта величина варьирует в широких пределах: от нескольких минут у бактерий до нескольких тысячелетий у древесных растений (секвойя). Обычно, чем крупнее растение или животное, тем больше их продолжительность жизни, хотя бывают и исключения (летучие мыши доживают до 30 лет, это дольше, например, жизни медведя).

Смертность и рождаемость у организмов весьма существенно изменяются с возрастом. Только увязав смертность и рождаемость с возрастной структурой популяции, можно вскрыть механизмы общей смертности и определиться со структурой продолжительности жизни. Такую информацию можно получить с помощью таблиц выживания, которые еще называют демографическими таблицами. Эти таблицы содержат сведения о характере распределения смертности по возрастам. Демография изучает размещение, численность, состав и динамику народонаселения, а таблицы она использует для определения ожидаемой продолжительности жизни человека.

Данные таблиц выживания позволяют построить кривые выживания (дожития), так как они отражают зависимость количества доживших до определенного возраста особей от продолжительности этого интервала с самого момента от рождения организмов.

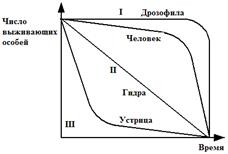Выделяют три типа основных кривых выживания (рис. 2.1), к которым в той или иной мере приближаются все известные кривые.

Кривая I типа, когда на протяжении всей жизни смертность ничтожно мала, резко падая в конце, характерна для насекомых, которые обычно гибнут после кладки яиц (ее и называют «кривой дрозофилы»), к ней приближаются кривые выживания человека в развитых странах, а также некоторых крупных млекопитающих.

Кривая III типа – это случаи массовой гибели особей в начальный период жизни. Гидробионты и некоторые другие организмы, незаботящиеся о потомстве, выживают за счет огромного числа личинок, икринок, семян и т.п. Моллюски, прежде чем закрепиться на дне, проходят личиночную стадию в планктоне, где личинки гибнут в огромных количествах, поэтому кривую III называют еще «кривой устрицы».

Кривая II типа (диагональная) характерна для видов, у которых смертность остается примерно постоянной в течение всей жизни. Такое распределение смертности не столь уж редкое явление среди организмов. Встречаются они среди рыб, пресмыкающихся, птиц, многолетних травянистых растений.

Реальные кривые выживания часто представляют собой некоторую комбинацию указанных выше основных типов. Например, у крупных млекопитающих, да и у людей, живущих в отсталых странах, кривая I вначале круто падает за счет повышенной смертности сразу после рождения.

Экспоненциальная модель численности популяций

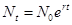→ , (2.5)

где N_t –численность популяции в момент времени; N₀– численность популяции в начальный момент времени t₀; r – показатель, характеризующий скорость размножения (прирост) особей в данной популяции. Экспоненциальный рост возможен только тогда, когда r имеет постоянное численное значение, так как скорость роста популяции пропорциональна самой численности.

Обсуждению важности вывода Мальтуса для популяционной динамики Ч. Дарвин посвятил несколько страниц своего дневника, указывая, что поскольку ни одна популяция не размножается до бесконечности, должны существовать факторы, препятствующие такому неограниченному размножению. Среди этих факторов может быть нехватка ресурса (продовольствия), вызывающая конкуренцию внутри популяции за ресурс, хищничество, конкуренция c другими видами. Результатом яв-ляется замедление скорости роста популяции и выход ее численности на стационарный уровень. Таким образом, экспоненциальный рост численности популяции – это рост численности ее особей в неизменяющихся условиях.

Условия, сохраняющиеся длительное время постоянными, невозможны в природе. Если бы это было не так, то, например, обычные бактерии могли бы дать такую массу органического вещества, которая могла бы покрыть весь земной шар слоем толщиной в два метра за два часа. Однако такого в природе не происходит, так как существует множество ограничивающих факторов. Но есть примеры, когда при замедлении роста, т.е. при снижении r, экспоненциальный рост сохраняется, может он возникать и на коротких отрезках жизни популяций.

Чтобы иметь полную картину динамики численности популяции, а также рассчитать скорость ее роста, необходимо знать величину так называемой чистой скорости воспроизводства(R₀), которая показывает, во сколько раз увеличивается численность популяции за одно поколение, за время его жизни Т:

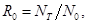(2.6)

где N_T – численность нового поколения; N₀– численность особей предшествующего поколения; R₀– чистая скорость воспроизводства, показывающая также, сколько вновь родившихся особей приходится на одну особь поколения родителей. Если R₀= 1, то популяция стационарная и численность ее сохра­няется постоянной. Скорость роста популяции обратно пропорциональна длительности поколения:

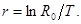(2.7)

Из последнего выражения следует, что чем раньше происходит размножение организмов, тем больше скорость роста популяции. Это в равной степени относится и к популяции человека, отсюда – важность значения этой закономерности в демографической политике любого государства.

Ограниченный рост

Впервые системный фактор, ограничивающий рост популяции, описал Ферхюльст в уравнении логистического роста:

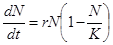. (2.8)

Это уравнение обладает двумя важными свойствами. При малых N численность х возрастает экспоненциально (как в уравнении 2.5) при больших – приближается к определенному пределу K, представляющему собой величину, называемую емкостью популяции, которая определяется ограниченностью пищевых ресурсов, мест для гнездования, многими другими факторами, которые могут быть различными для разных видов. Таким образом емкость экологической ниши представляет собой системный фактор,который определяет ограниченность роста популяции в данном ареале обитания.

Уравнение (2.8) можно также переписать в виде:

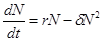, (2.9)

где δ –коэффициент внутривидовой конкуренции (за пищевой ресурс, убежища и т.п.). Решение уравнения (2.9) имеет вид:

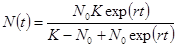(2.10)

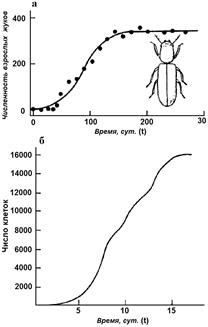Формула (2.10) представляет собой зависимость численности популяции от времени. Примеры экспериментально наблюдаемой динамики популяций, развивающихся по логистическому закону, приведены на рис. 2.2 а, б.

На рис. 2.2 а сплошной линией представлен график функции, которая описывается формулой (2.10). кривая N(t) имеет точку перегиба, с координатами:

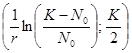
Ордината представляет собой половину максимальной численности, а абсцисса зависит как от емкости популяции K, так и от константы собственной скорости роста r – чем выше генетические возможности популяции, тем скорее наступает перегиб на кривой численности.

Логистическая модель Ферхюльста (2.8) оказалась весьма перспективной. Исследование этого уравнения в случае дискретного изменения численности в популяциях с неперекрывающимися поколениями показало целый спектр возможных типов решений, в том числе колебательные изменения разного периода и вспышки численности.

При описании развития популяций следует отметить биологический факт, заключающийся в том, что в природе популяции имеют не только максимальную численность, определяемую величиной экологической ниши K, но и минимальную критическую численность L. При падении численности популяции ниже этой критической величины из-за неблагоприятных условий, или в результате хищнического промысла, восстановление популяции становится невозможным.

Величина нижней критической плотности различна для разных видов. Исследования биологов показали, что она может составлять всего лишь пару особей на тысячу квадратных километров в случае ондатры, и сотни тысяч особей для американского странствующего голубя. Заранее трудно было предположить, что столь многочисленный вид уже перешел через критическую границу своей численности и обречен на вымирание. Например, для голубых китов критическая граница численности оказалась равной десяткам-сотням. Хищническое истребление этих гигантских животных привело к тому, что их осталось слишком мало в Мировом океане. И хотя охота на них давно запрещена, надежд на восстановление популяции голубых китов практически нет. Кривые показателей численности для трех видов китов приведены на рис. 2.3.

Модели, описывающие как внутривидовую конкуренцию, определяющую верхнюю границу численности популяции, так и нижнюю критическую численность популяции, имеют два устойчивых стационарных решения. Одно из них - нулевое для начальных численностей, которые ниже наименьшей критической численности популяции. Другое равно K - емкости экологической ниши в случае, когда начальная численность выше наименьшей критической величины. Такими «триггерными» свойствами обладает нелинейное уравнение, предложенное А.Д. Базыкиным.

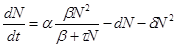(2.11)

В формуле (2.11) первый член в правой части описывает размножение двуполой популяции, скорость которого пропорциональна квадрату численности (вероятности встреч особей разного пола) для малых плотностей, и пропорциональна числу самок в популяции – для больших плотностей популяции. Второй член описывает смертность, пропорциональную численности, а третий – внутривидовую конкуренцию, подобно тому, как это было в логистическом уравнении (2.9).

Зависимости численности от времени и скорости прироста от численности представлены на рис. 2.4 (а, б). Кривые 1-5 соответствуют различным начальным значениям популяции x. x = 0 и x = K – устойчивые стационарные состояния, x = L – неустойчивое, разделяющее области влияния устойчивых состояний равновесия. Величины L и K различны для разных популяций и могут быть определены из наблюдений и экспериментов.

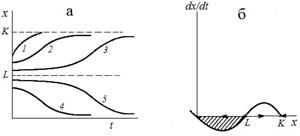
Рис.2.4. Модель популяции с нижней критической численностью. Зависимость численности популяции от времени (а) и скорости роста от численности (б) для модели (2.11). Штриховкой обозначена область вырождения популяции.

Из рис. 2.4 (а) видно, что скорость восстановления популяции после ее падения в силу промысла или неблагоприятных условий зависит от того, насколько близка новая начальная численность к опасной границе L. Если ущерб, нанесенный популяции невелик (меньше половины емкости экологической ниши) популяция быстро восстанавливается по кривой 1, не имеющей точки перегиба. В случае, когда численность оставшейся популяции близка к критической, восстановление происходит сначала очень медленно, популяция надолго «застревает» вблизи опасной границы, а затем уже, «набрав силы», более быстро выходит на устойчивый стационарный уровень K (кривая 3). Кривая 2 представляет промежуточный случай. Кривые 4, 5 иллюстрирует вырождение популяции в случае, когда начальная численность опустилась ниже критической границы. обращает на себя внимание сходства начальных участков кривых 3 и 5. Близость к опасной границе со стороны больших значений (3) и меньших (5) выражается в долгом пребывании системы в неопределенном состоянии, когда малые флуктуации могут легко «перебросить» систему через опасную границу в «благополучную» область возврата к стационарному значению K,или, наоборот, в область вымирания.

В это время сторонний наблюдатель не сможет определить по форме кривой динамики численности, какая судьба ожидает систему. Для самих участников жизненной драмы – нахождения системы вблизи опасной границы – исход не очевиден. Важно понимать, что в этой ситуации чрезвычайно важны любые, даже очень малые усилия, направленные на преодоление критического барьера.

Именно популяции, численность которых близка к нижней критической численности, занесены в Красную книгу. Удастся ли перенести каждый конкретный вид на «Зеленые страницы», куда переносят виды, исчезновение которых удалось предотвратить, зависит от многих обстоятельств, в частности, как от репродуктивных усилий вида, так и от усилий людей, спасающих эти виды.

Анализ S – образной кривой (рис.2.2 (а) или рис.2.4 (а) кривая 2) показывает, что воздействие экологических факторов на скорость роста популя­ции может довести численность популяции до стабильной (r = 0), либо ее уменьшить, т.е. экспоненциальный рост замедляется или останавливается полностью и криваяэкспоненциального роста как бы вырождается в S-образнуюкривую.

В природе так и происходит: экспоненциальный рост наблюдается какое-то достаточно корот- кое время, после чего ограничивающие факторы его стабилизируют и дальнейшее развитие популяции идет по логистической модели, что и описывается S-образной, логистической кривой роста популяции. Однако плато на S-образной кривой далеко не всегда бывает гладким, потому что колебания численности происходят постоянно, что отражается в виде колебаний кривой вокруг асимптоты «К» (рис. 2.5), эти колебания называются флуктуациями численности, которые могут быть сезонными и годовыми. Первые обусловлены абиотическими факторами, вторые – плюс к этому, еще и внутренними, биотическими. Колебания, вызванные биотическими факторами, называют осцилляциями 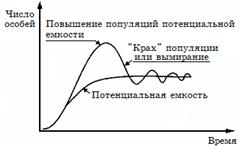(рис. 2.6), они отличаются высокой регуляцией и их даже называют циклами. Многие факторы, природные и антропогенные, вызывающие флуктуации, в значительной мере можно учесть, введя в формулу поправочные коэффициенты. Такие формулы позволяют прогнозировать реальный рост популяции живот ных и подобные процессы в демографии людского населения.

Влияние запаздывания

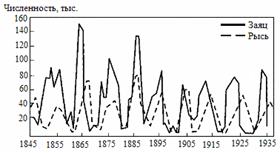Уравнения, которые мы рассматривали до сих пор, предполагают, что процессы размножения и гибели происходят одновременно и популяция мгновенно реагирует на любое изменение внешних условий. Однако в реальности это не так. Всегда имеется некоторое запаздывание, которое вызвано несколькими причинами.

Развитие любой взрослой особи из оплодотворенного яйца требует определенного времени T. Поэтому если какое-нибудь изменение в окружающей среде, например, увеличение ресурса, вызовет внезапное повышение продуктивности взрослых особей, то соответствующе изменение численности произойдет лишь по прошествии времени T. Это означает, что уравнение

dN/dt = f(N), (2.12)

где N – численность взрослых особей, следует заменить уравнением:

dN/dt = f(N_t-T), (2.13)

где x_t-T – численность половозрелых особей в момент t-T.

В реальных популяциях интенсивность размножения и гибели различны в разных возрастных группах. Например, у насекомых откладывают яйца взрослые особи, а конкуренция наиболее выражена на личиночной стадии. Такие процессы, как отравление среды продуктами метаболизма, каннибализм и т.п. в наиболее сильной степени воздействуют на ранние возрастные стадии, а их интенсивность зависит от численности взрослых особей, т.е. отрицательное влияние на коэффициент естественного прироста оказывают особи предыдущего поколения. С учетом этих обстоятельств, логистическое уравнение (2.9) перепишется в виде:

dN/dt = N(r-N_t-T). (2.14)

Наиболее распространенное и изученное в динамике популяций уравнение Хатчинсона учитывает тот факт, что особи размножаются лишь с определенного возраста, и имеет вид:

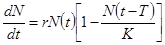(2.15)

Смысл модели (2.15) заключается в том, что уровень лимитирования системы зависит не только от общей численности популяции в данный момент времени t, определяемой емкостью среды, но и от количества половозрелых особей в момент времени t-T. Еще более точное уравнение, учитываю-

щее распределение времени запаздывания:

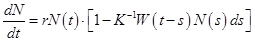. (2.10)

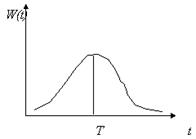
Вид функции распределения времен запаздывания W(t-s) представлен на рис. 2.7. Такого типа уравнения могут иметь колебательные решения.

В технике хорошо известно, что запаздывание в регуляции системы может привести к возникновению колебаний решения. Если система регулируется петлей обратной связи, в которой происходит существенная задержка, то весьма вероятно возникновение колебаний. Если продолжительность задержки в петле обратной связи больше собственного времени системы, могут возникнуть колебания с нарастающей амплитудой, нарушаются их период и фаза. Вопросы регуляции плотности и дискретные модели популяций даны в приложения 3, П.2, П.3.