Кеплердің үшінші (түзетілген) заңы
Дөңгелектік қозғалыс кезінде үдеу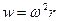 
, мұндағы бұрыштық жылдамдық 
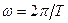, ал 
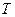- айналу периоды болса, онда үдеу былайша анықталады:
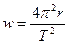(2.1.11)
Массасы m аспан денесінің массасы М орталық денені шеңбер бойымен айнала қозғалысын қарастырайық, олай болса жоғарыдағы өрнекке сәйкес салыстырмалы үдеу мынаған тең:
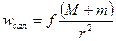, (2.1.12)
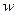және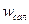 
– екеуі бір шама, яғни үдеу болғандықтан, теңдеулердің оң жақтарын теңестіріп, келесі өрнекті аламыз:
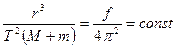(2.1.13)
Аспан дененсінің қозғалысын эллипс бойымен қарастырсақ, сонда (2.1.13) өрнекке ұқсас өрнекті аламыз, бірақ мұнда шеңбер радиусы r үлкен жарты ось а-ға алмастырылады, ал Т дененің эллипс бойымен айналу периодын білдіреді. Осы өрнекті массалары m және m2 екі дене үшін жазайық, олардың эллипстік орбиталарының үлкен жарты осьтері а1 және а2, ал айналу периодтарын Т1 және Т2 деп белгілесек, сонда:
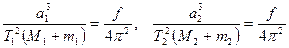(2.1.14)
Бұл Кеплердің 3-ші заңының түзетілген түрі. Егер екі планетаның Күнді айнала қозғалысын қарастырсақ, яғни М1=М2 болса және планеталар массасы Күн массасымен салыстырғанда ескермейтіндей аз болса (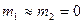 
), онда Кеплердің бақылаулар нәтижесінде алған өрнегіне келеміз:
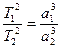(2.1.15)
(2.1.13) және (2.1.14) өнектерінің астрономиядағы маңызы өте зор, өйткені олар аспан денелерінің массаларын аңықтауға мүмкіндік береді.
Дата добавления: 2015-05-16; просмотров: 2184;