RC-генераторы
Для генерирования колебаний низких частот применяются фазосдвигающие RC-цепи, так как они имеют меньшие габариты и вес, чем LC -схемы. Три RC - цепочки (рис. 9.17, а) дают фазовый сдвиг минус 180о между напряжением на входе и выходе. Этот фазовый сдвиг получается на частоте
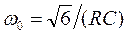. (9.27)
а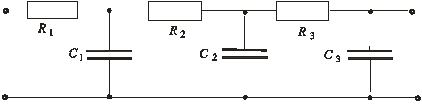 
Трехзвенная RC – цепочка с положительным фазовым сдвигом на 180º приведена на рис. 9.17, б.
б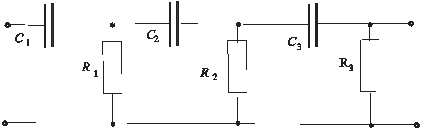 
Рис. 9.17
Частота квазирезонанса:
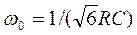(9.28)
Генератор с фазосдвигающими RС- цепочками показан на рис. 9.18
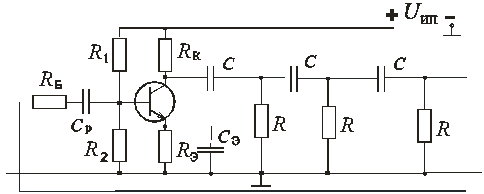
Рис. 9.18
Для данной схемы условие баланса фаз выполняется на частоте
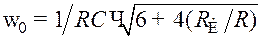(9.29)
баланс амплитуд приводит к условию 
.
RC-генератор с мостом Вина имеет следующий вид, представленный рис. 9.19, АЧХ приведена на рис. 9.20.
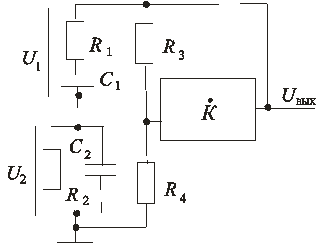
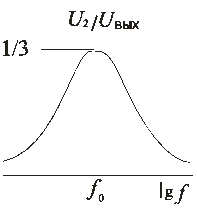
Рис. 9.19 Рис. 9.20
:
Коэффициент передачи цепи обратной связи
, (9.30)
тогда получим
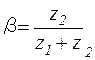, (9.31)
если R1 = R2 = R; С1 = С2 = С, то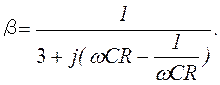 
(9.32)
Чтобы фазовый сдвиг был равен нулю, необходимо чтобы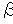 
было вещественным, т.е.
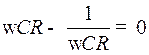, 1=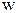 
2С2R2.
Отсюда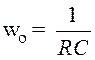 
(9.33)
Схема с использованием моста Вина (рис. 9.21) в зависимости от величины сопротивления RОС, может работать как в режиме избирательного усиления, так и в режиме генерации.
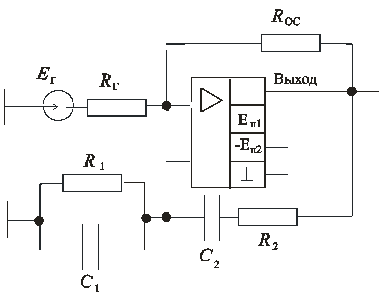
Рис. 9.21
Схема двойного Т- образного моста имеет следующий вид, представленный на (рис. 9.22):
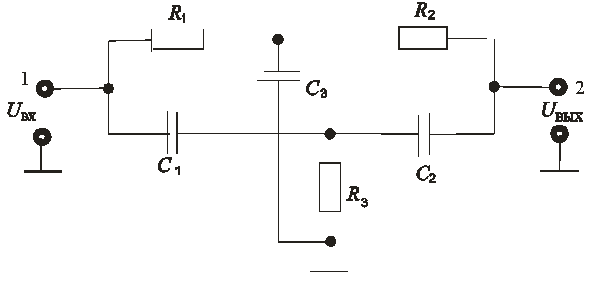
Рис. 9.22
Так как двойной Т-мост имеет характеристику, обратную резонансной (рис. 9.23), то для получения избирательности его необходимо включать в цепь отрицательной обратной связи (рис. 9.24). Сам усилитель не должен вносить частотных искажений.
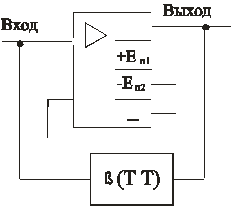
Рис. 9.23 Рис. 9.24
То есть, на резонансной частоте избирательность усилителя и, следовательно, добротность возрастают:
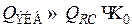. (9.34)
По аналогии с уравнениями для избирательной LC схемы:
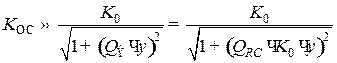, (9.35)
т.е. видно, что избирательность усилителя зависит от коэффициента усиления рис. 9.23.
Устойчивость и качество работы зависят от настройки:
1) мост должен быть сбалансирован так, чтобы на частоте настройки его коэффициент передачи был равен нулю.
2) обе ветви частотных характеристик, построенные в логарифмическом масштабе, должны быть симметричны. Это обеспечивает устойчивость работы и отсутствие паразитных колебаний.
На практике обычно:
R1 = R2 = R; C 1 = C2 = C.
Тогда условие баланса:
; 
; 
; 
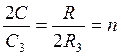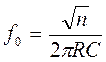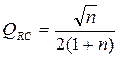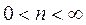` (9.36)
Условие баланса моста сводится к тому, что проходное сопротивление между точками 1 и 2 (рис. 9.22) должно быть равно бесконечности на частоте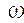 
0 или величина проходной проводимости равнялась нулю.
Это условие приводит к равенствам:
,
.
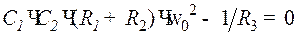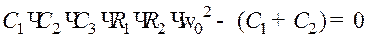Коэффициент передачи моста:
. (9.37)
где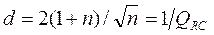 
− затухание,
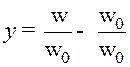– относительная расстройка.
Частотная характеристика:
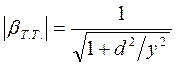. (9.38)
Фазовая характеристика:
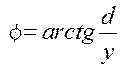; (9.39)
Добротность максимальна при n = 1; QRC = 0,25.
При равенстве всех резисторов и конденсаторов QRC = 0,236.
Условие симметрии выполняется автоматически только при ZГ и ZН =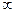 
. Поэтому необходимо учитывать влияние ZГ и ZН. При наличии, например, только СГ или СН симметрирование моста невозможно.
Включение двойного Т-моста «в ножку» с использованием ОУ имеет вид как на (рис. 9.25).
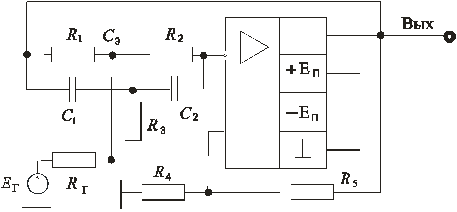
Рис. 9.25
Резонансная частота для данной схемы определяется по формуле:
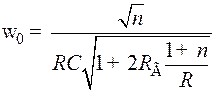; (9.40)
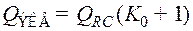; (9.41)
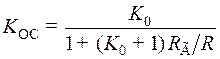; (9.42)
Желательно выбирать RГ поменьше, соблюдая условие: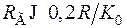 
.
Дата добавления: 2015-05-13; просмотров: 2369;