Переходы металл-полупроводник
Переходы металл-полупроводник используются для создания полупроводниковых диодов (диодов Шотки), а также для создания омических переходов (контактов), являющихся неотъемлемой частью любого полупроводникового прибора.
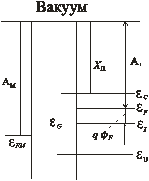
На рис. 1.10, а энергетические зонные диаграммы металла и полупроводника рассмотрены изолированно, металл и полупроводник не приведены в соприкосновение друг с другом и их система не находится в термодинамическом равновесии.
а б
в г
Рис. 1.10
Для полупроводника минимальная энергия для удаления электрона со дна зоны проводимости в вакуум называется энергией электронного сродства 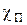 , или истинной работой выхода.
, или истинной работой выхода.
Величина АП, равная разности энергий, соответствующих уровню Ферми полупроводника εF и уровню энергии вакуума, называется термоэлектронной работой выхода. Если обозначить разницу между уровнями Ферми εF и уровнем Ферми в собственном полупроводнике εi через qφF = εF – εi,
то, как следует из рис. 1.10, а, величины χП и АП связаны между собой выражением (для n-полупроводника):
АП = χП + εG / 2 – qφF (1.45)
Таким образом, термоэлектронная работа выхода АП в отличие от χП зависит от степени легирования полупроводника через зависимость
φF = φT ln(Nd / ni ) (1.46)
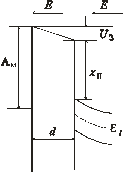
Если металл и полупроводник соединить внешней цепью, то по ней из полупроводника в металл перетечет некоторое количество электронов, установится термодинамическое равновесие, энергия уровня Ферми станет постоянной во всей системе (рис. 1.10, б). В зазоре между металлом и полупроводником и в приповерхностном слое полупроводника возникнет электрическое поле, обусловленное тем, что на внутренней поверхности металла накопятся электроны, а на поверхности полупроводника обнажится заряд нескомпенсированных положительных ионов доноров. Разность потенциалов в зазоре будет определяться соотношением UЗ = dEЗ, где d – толщина зазора, EЗ – напряженность электрического поля в зазоре. Обеднение поверхности полупроводника электронами в приповерхностном слое приведет к изгибу зон вверх.
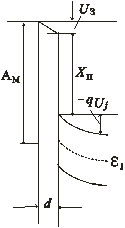
При сближении металла и полупроводника UЗ→0, так как EЗ – конечная величина (рис. 1.10, в). Когда металл и полупроводник в конце концов придут в контакт, то барьер, обусловленный зазором, исчезнет (UЗ = 0) и получится идеальный переход металл-полупроводник (рис. 1.10, г). Высота потенциального барьера для электронов, переходящих из металла в полупроводник, будет в этом случае определяться соотношением:
UВ = (АМ – χП) / q (1.47)
Для большинства реальных контактов идеальная ситуация, изображенная на рис. 1.10, г, никогда не выполняется, так как на поверхности полупроводника обычно существует тонкий диэлектрический слой толщиной 0,5…2,0 нм, который называют промежуточным. Для кремния промежуточный слой является слоем диоксида кремния (оксида) и обусловлен технологическими причинами. Таким образом, реальные контакты больше соответствуют случаю, приведенному на рис. 1.10, б. Однако толщина барьера для электронов, обусловленного слоем оксида, настолько мала, что электроны могут легко туннелировать сквозь него. Кроме того, падение напряжения 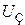 на пленке оксида настолько мало, что уравнение (1.47) является хорошей аппроксимацией для высоты барьера.
на пленке оксида настолько мало, что уравнение (1.47) является хорошей аппроксимацией для высоты барьера.
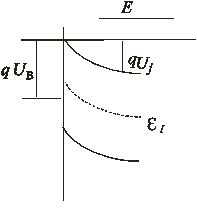
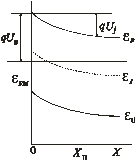
Высота потенциального барьера для электронов, переходящих из полупроводника в металл qUJ, определяется изгибом зон в полупроводнике (рис. 1.10, г), где UJ носит название контактной разности потенциалов. Ее величина, как следует из рассмотрения рис. 1.10:
UJ = (АМ – AП) / q (1.48)
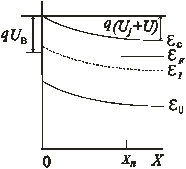
При принятом соотношении Ам >Ап приповерхностная область полупроводника становится обедненной электронами. Под действием электрического поля электроны уходят из этой области, оставляя нескомпенсированный заряд положительных ионов доноров. При достаточно большой высоте барьера концентрация электронов, а также дырок в некоторой приповерхностной области полупроводника (при 0 < Х < Хn) оказывается много меньше концентрации ионов доноров ND (рис. 1.11, а).
а б в
Рис. 1.11
Поэтому такую область называют областью пространственного заряда (ОПЗ), или обедненной областью.
Рассмотрим, что произойдет, если к переходу металл-полупроводник приложить внешнее напряжение U. Так как ОПЗ обеднена носителями заряда, ее сопротивление велико и практически все напряжение U прикладывается к этой области.
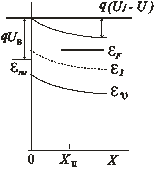
Если к металлу подключен положительный полюс источника напряжения U, то поле в ОПЗ перехода уменьшится, высота потенциального барьера станет равной (UJ – U) и толщина ОПЗ сократится. Это случай прямогосмещения перехода (рис. 1.11, б).
Если к металлу подключить отрицательный полюс источника напряжения U, то напряженность электрического поля в ОПЗ увеличится, разность потенциалов на ОПЗ возрастет до величины (UJ + U). Возросшее электрическое поле будет оттягивать вблизи границы Xn электроны из квазинейтральной области полупроводника и перенесет их через внешнюю цепь в металл, вследствие чего толщина ОПЗ увеличится, как показано на рис. 1.11, в. Такое включение перехода М–П называют обратным.
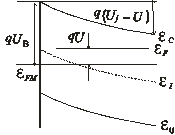
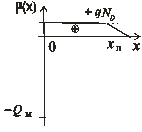
Толщину области пространственного заряда Xn, распределение электрического поля и потенциала в ОПЗ можно определить с помощью решения уравнения Пуассона, предположив, что в ОПЗ концентрация дырок и электронов много меньше концентрации доноров (рис. 1.12, б) 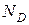 , граница между ОПЗ и нейтральной областью резкая и напряженность электрического поля Е(Хn) = 0 как показано на рис. 1.12, в. Энергетическая зонная диаграмма приведена на рис. 1.12, а.
, граница между ОПЗ и нейтральной областью резкая и напряженность электрического поля Е(Хn) = 0 как показано на рис. 1.12, в. Энергетическая зонная диаграмма приведена на рис. 1.12, а.
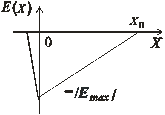 а б в
а б в
Рис. 1.12
Обычно в рабочем диапазоне температур (от – 60 до +125°С) атомы донорной примеси полностью ионизованы, поэтому объемный заряд в ОПЗ
ρ = +qND и уравнение Пуассона принимает вид
ε ε0 (dE / dx) = qND (1.49)
Взяв интеграл с помощью разделения переменных, можно получить
E(x) = qND (x – xn) / (ε ε0) (1.50)
Распределение Е(X) изображено на рис. 1.12, в. Разность потенциалов на ОПЗ составляет (UJ – U), поэтому
UJ – U = – ∫0 xn (x)dx = | Emax| /2 = qND xn2/ (2 ε ε0) (1.51)
Из последнего соотношения можно определить
xn = [(2 ε ε0) (UJ – U)/(qND)]1/2, (1.52)
Emax = 2(UJ – U) / xn = [2qND (UJ – U) /( ε ε0)]1/2 (1.53)
Перейдем к рассмотрению вольт-амперной характеристики (ВАХ) диода Шотки, т.е. функциональной зависимости тока диода от приложенного напряжения. Теория ВАХ диода Шотки базируется на теории термоэлектронной эмиссии электронов.
Обозначим плотность тока термоэлектронной эмиссии электронов из металла в полупроводник JМ-П и, наоборот, из полупроводника в металл JП -М. Как известно, плотность тока термоэлектронной эмиссии из металла в вакуум определяется формулой Ричардсона – Дэшмана.
J = АR T2 exp (–АM / kT) , где (1.54)
АR = 4π g m*k2 /h3 – постоянная Ричардсона; m*– эффективная масса электрона; k – постоянная Больцмана; h – постоянная Планка; Т – абсолютная температура, К.
В приближении свободных электронов m* = m0 = 9,1∙10-31кг, значение АR = 120 A/(см2К2)
Если промежуточный диэлектрический слой между металлом и полупроводником туннельно тонок, то для перехода из металла в полупроводник электронам нужно преодолеть потенциальный барьер высотой qUB, как показано на рис. 1.10, г. Воспользовавшись формулой (1.54) с учетом того, что в данном случае высота потенциального барьера равна не АM, а qUB, запишем:
JМ-П = АR T2exp (– qUB / kT) (1.55)
Поскольку все внешнее напряжение U падает на запирающем слое (ОПЗ), то величина qUB со стороны металла, а значит и JМ-П не зависят от U. В состоянии термодинамического равновесия JМ-П = JП-М и поэтому JП-М = АR T2exp (–qUB / kT). При наличии внешнего прямого смещения высота потенциального барьера для электронов, текущих из полупроводника в металл, уменьшится на величину U, поэтому
JП-М = АR T2exp (–q(UB –U)/ kT) (1.56)
Результирующая плотность тока через диод J = JМ-П – JП-М. Учитывая, что площадь перехода М–П равна S, окончательно записываем выражение для JS ВАХ диода Шотки:
I = S JS [exp (qU / kT) – 1] = IS [exp (U / φT) – 1] (1.57)
В последнем выражении предэкспоненциальный множитель определяется формулой
JS = АR T2exp (–qUB / kT) (1.58)
В соответствии с (1.57) при прямом смещении (U > 0) прямой ток экспоненциально увеличивается с ростом U. При обратном включении (U < 0) ток диода стремится к постоянному значению –IS = – S JS .
В реальных диодах Шотки зависимость высоты барьера qUB значительно слабее зависит от работы выхода АM, чем это следует из (1.47). Это обусловлено тем, что в нижней трети запрещенной зоны полупроводников имеется большое количество поверхностных состояний, которые могут принять на «себя» (захватить) большое количество электронов, переходящих из металла. В этом случае поверхностные состояния, захватывая электроны из объема полупроводника, создают обеднение на поверхности и достаточно сильный изгиб зон, фиксируя уровень Ферми полупроводника в нижней трети запрещенной зоны.
В системе с металлом эти поверхностные состояния, захватывая электроны металла, как бы экранируют объем полупроводника, в результате чего высота барьера qUB слабо зависит от значения АM металла и не обнаруживает четких изменений в функции концентрации доноров. Другое явление заключается во влиянии сил «изображения» при переходе электронов из полупроводников в металл. Это эквивалентно понижению высоты потенциального барьера, которое наиболее сильно сказывается при обратных смещениях перехода М–П, приводя к нарушению постоянства IS.
Структуры, именуемые структурами с барьером Шотки, создаются методами планарной технологии, когда все технологические процессы осуществляются только на одной и той же поверхности полупроводниковой пластины. На поверхность полупроводника, предварительно обработанную химическим травлением, полировкой или сколом в вакууме, наносится слой металла с помощью анодирования, термического испарения и конденсации в вакууме или методами электронно-лучевой бомбардировки. Толщина промежуточного слоя, возникающего между поверхностями полупроводника и металла, либо равна нулю, либо имеет порядок межатомных размеров и является туннельно-прозрачной для электронов.
В табл. 1.3 показаны возможные сочетания полупроводника с металлом и свойства структур,
Таблица 1.3
| Тип проводимости | Соотношения работ выхода | Характер структуры |
| Дырочный Дырочный | Wop > WOM Wop < WOM | Выпрямляющий Омический (невыпрямляющий) |
| Электронный Электронный | WOn < WOM WOn > WOM | Выпрямляющий Омический (невыпрямляющий) |
где Wop,n– работа выхода соответственно дырочного или электронного по- лупроводника;
WOM – работа выхода металла.
Таким образом, вольт-амперные характеристики структур определяются термодинамической работой выхода металла и полупроводника. В зависимости от типа проводимости полупроводника и соотношений работ выхода металла и полупроводника, структура может оказаться невыпрямляющей и ее вольт-амперная характеристика – линейна, или выпрямляющей с нелинейной характеристикой, как в резком электронно-дырочном переходе.
Дата добавления: 2015-05-13; просмотров: 2350;
