Задание 4. Обеспечьте ввод переменных с приглашением. Объявите с инициализацией переменную для полупериметра.

После объявления переменной S для площади необходимо её инициализировать

Набрав слово Math или вызвав подсказчик, видим, что среда требует исправить ошибки.

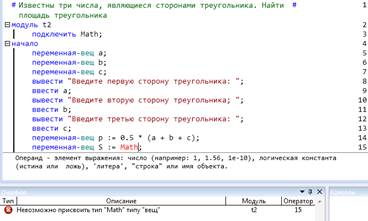
Это легко сделать, поставив точку (операция доступа к методам библиотеки) после имени библиотеки

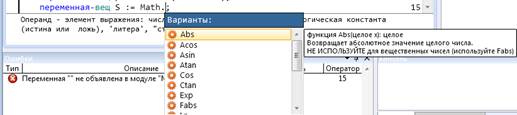
Математическая библиотека включает в себя большое количество функций, для каждой имеется подсказка. Выбрать нужную функцию можно с помощью клавиш управления курсором, а можно начать набирать нужное имя sqrt

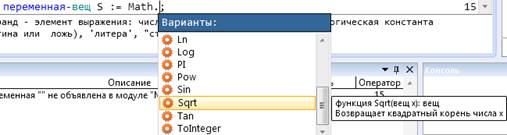
В подсказке приведён прототип функции имя, в скобках список формальных параметров с указанием типа этих параметров, после двоеточия тип возвращаемого значения.

При вызове функции после имени функции следует в скобках список фактических параметров – в нашем случае параметр один – арифметическое выражение.

Задание 5. Объявите с инициализацией переменную для площади. Выведите результат на экран, используя оператор вывода. Для отделения входных данных от результата используйте строковую константу, состоящую из необходимого числа произвольных символов.

Выведите пояснение к результату – надпись, гласящую, что число на экране – площадь треугольника.

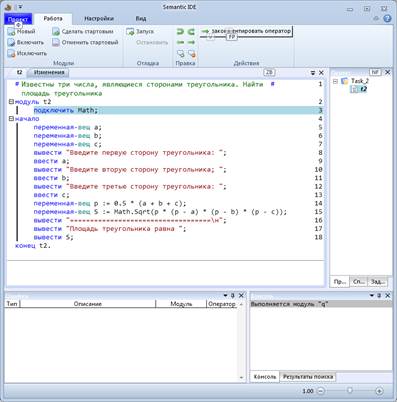
Прежде, чем запускать программу на выполнение и вводить данные, подумаем, что будем вводить.

Можно, конечно, ввести три какие-нибудь числа, но мы не будем знать, правильно ли программа рассчитала, черный ли сообщила результат. Считать на калькуляторе по формуле Герона – не очень увлекательное занятие. Лучше подобрать такие данные, чтобы обойтись без громоздких расчётов.

1.Например, всем известен египетский треугольник – с катетами 3 и 4 и гипотенузой 5. Его площадь равна половине произведения катетов, то есть 6.

2.Если уменьшить длины сторон в 10 раз, то площадь уменьшится в 100 раз, поэтому для набора 0,3, 0,4, 0,5 ожидается результат 0,06.

3.Легко вычислить площадь прямоугольного треугольника с катетами 1, 1 и гипотенузой 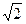(приблизительно 1,41412), площадь равна 0,5

4.Если вспомнить, что площадь правильного треугольника со стороной a равна 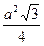, то набор 2, 2, 2 должен дать результат 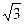(приблизительно 1,73).

5.Кроме того, треугольник со сторонами 1, 2, 3 – собственно говоря, не треугольник, а отрезок длиной три единицы с точкой, делящеё его на две части. И площадь у него должна быть равна нулю.

6.Аналогичный результат – например, для набора 5, 0, 5 или 0, 0, 0.

7.А вот треугольника со сторонами 1, 2, 4 быть не может – нарушено так называемое неравенство треугольника: каждая сторона должна быть меньше, чем сумма двух других сторон. При подсчёте по формуле Герона под корнем окажется отрицательное число, потому что полупериметр равен 3,5, а вычитать придётся 4.

8.И уж совсем негодные данные, содержащие хотя бы одно отрицательное число.

Первые четыре набора – допустимые данные.

Пункты 5 и 6 – примеры пограничных наборов данных, это случаи так называемого вырожденного треугольника

Пункты 7 и 8 – примеры недопустимых наборов данных.

Теперь можно приступать к тестированию. Если бы мы работали в какой-нибудь другой среде, а не в Semantic IDE, то вряд ли к тестированию мы смогли бы приступить так быстро. Даже в такой маленькой программе легко наделать множество опечаток, а найти и устранить их сложно.

Набор текста программы посимвольно более привычен, но и более чреват разнообразными опечатками, его можно сравнить с постройкой небоскрёба из кирпичей. Неровно уложенный кирпич и не заметен, но приводит к угрозе разрушения или даже сразу к разрушению. Семантический редактор предлагает готовые блоки – качественные; Конечно, важно их правильно установить, но редактор сразу проверяет семантически неверные конструкции и подаёт сигнал устранить ошибку.

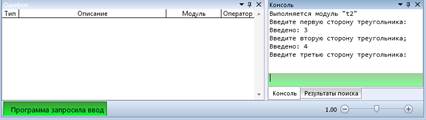
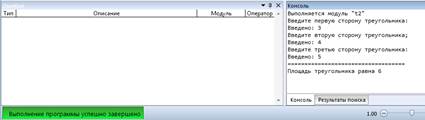
3.3.8 Задание 6. Запустите программу на выполнение. Введите поочерёдно первый, четвёртый, пятый и шестой наборы данных. Убедитесь, что результаты работы программы совпадают с ожидаемыми.

Прежде, чем водить второй и третий наборы, обратим внимание на результат работы четвёртого теста:

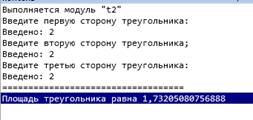
В консоли дробная часть вещественного числа отделена запятой, а в коде обязательно ставить точку. Что же нужно вводить, если возникла необходимость ввести дробные значения?

Будем вводить третий набор, используя запятую:

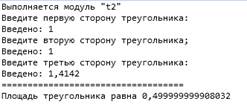
Результат практически совпал с ожидаемым. Тем более, что гипотенуза введена с точностью 4 знача после запятой, остальные отброшены, поэтому результат и меньше, чем ожидаемые 0,5. Правда, очень не на много.

Введем ещё раз третий набор, только используем десятичную точку результат сохранился,