Введение в теорию конечных автоматов

Основные понятия теории автоматов

Все рассмотренные выше устройства относятся к классу комбинационных схем, то есть дискретных устройств без памяти. Наряду с ними в цифровой технике широкое распространение получили последовательностные автоматы или иначе комбинационные схемы, объединенные с элементами памяти.

Под термином автомат можно понимать как некоторое реально существующее устройство, функционирующее на основании как сигналов о состоянии внешней среды, так и внутренних сигналов о состоянии самого автомата. В этом плане ЭВМ может быть рассмотрена как цифровой автомат. Под цифровым автоматом понимается устройство, предназначенное для преобразования цифровой информации. С другой стороны под термином автомат можно понимать математическую модель некоторого устройства. Общая теория автоматов подразделяется на две части - абстрактную и структурную теорию автоматов. Различие между ними состоит в том, что абстрактная теория абстрагируется от структуры, как самого автомата, так и входных и выходных сигналов. В абстрактной теории анализируются переходы автомата под воздействием абстрактных входных слов и формируемые на этих переходах абстрактные выходные слова.

В структурной теории рассматривается прежде всего структура как самого автомата, так и его входных и выходных сигналов, способы построения автоматов из элементарных автоматов, способы кодирования входных и выходных сигналов, состояний автомата.

В соответствии с этим принято различать две модели автоматов: структурная и абстрактная. Абстрактная модель применяется при теоретическом рассмотрении автоматов. Структурная модель служит для построения схемы автомата из логических элементов и триггеров, и предназначена для выполнения функции управления.

Абстрактный автомат – это математическая модель цифрового автомата, задаваемая шестикомпонентным вектором S=(A,Z,W,d,l,a₁),

где А={a_a,…,a_m} – множество внутренних состояний абстрактного автомата, Z=[z₁,…,z_k} и W={w₁,…,w_l} – соответственно множества входных и выходных абстрактных слов, d - функция переходов, l - функция выходов, a₁ – начальное состояние автомата. Абстрактный автомат может быть представлен как устройство с одним входом и одним выходом (рис. 34) на которые подаются абстрактные входные слова и формируются абстрактные выходные слова:

Понятие состояния автомата используется для описания систем выходы которых зависят не только от входных сигналов, но и от предыстории, то есть информации о том что происходило с автоматом в предыдущий интервал времени. Состояние автомата позволяет устранить время как явную переменную и выразить выходные сигналы как функцию состояний и входных сигналов.

По виду функции выходов все множество автоматов можно подразделить на два класса: автоматы Мили и автоматы Мура.

Автоматами Мили или автоматами первого типа называют автоматы, для которых выходной символ w(t) не завит явно от входного символа z(t), а определяется только состоянием автомата в момент времени t. Закон функционирования автомата Мура может быть описана системой уравнений.

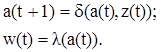
К автоматам второго типа или автоматам Мили, относятся автоматы поведение которых может быть описано системой уравнений.

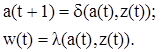
Следовательно, в отличие от автомата Мура для автомата Мили выходной символ w(t) зависит не только от текущего состояния, но и от входного символа.

Между моделями автоматов Мили и Мура существует соответствие позволяющее преобразовать закон функционирования одного из них в другой.

Совмещенная модель автомата (С-автомат). Абстрактный С-автомат – математическая модель дискретного устройства определяемого вектором S=(A,Z,W,U,d,l₁,l₂,a₁), где А, Z, d и а₁ – определены выше, а W={w₁,…,w_l} и U={u₁,…,u_l} – выходной абстрактный алфавит автомата Мили и Мура соответственно, l₁ и l₂ - функции выходов. Абстрактный С-автомат может быть представлен как устройство с одним входом на который поступают слова из входного алфавита X и двумя выходами (рис. 35), на которых формируются абстрактные входные слова из выходных алфавитов W и U.

Отличие С-автомата от моделей автоматов Мили и Мура заключается в том, что он одновременно реализует две функции выходов l₁ и l₂ каждая из которых характерна для одной из двух моделей.

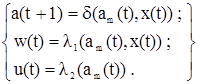
Автомат S называется конечным, если конечны множества A, Z и W и детерминированным, если находясь в некотором состоянии он не может перейти более чем в одно состояние под действием одного и того же входного символа. Состояние а_s называется устойчивым, если для любого z_kÎZ такого, что a_s=d(a_m,z_k) a_s=d(a_s,z_k). Автомат S является асинхронным, если каждое его состояние устойчиво, иначе синхронным.

Автомат называется полностью определенным, если область определения функции d совпадает с множеством пар (a_m,z_k), f функции l для автомата Мили с множеством пар (a_m,z_k), Мура с a_m. У частичного автомата функции d и l определены не для всех пар. Автомат является инициальным если в нем выделено начальное состояние а₁.