Гидравлически наивыгоднейшее сечение канала
Гидравлически наивыгоднейшей называется такая форма поперечного сечения русла, которая при заданных площади сечения канала и шероховатости дает наибольшую пропускную способность.
Если взять ряд живых сечений различной формы, но одинаковой площади  и шероховатости, то наивыгоднейшим из них будет то сечение, которое при том же уклоне будет пропускать наибольший расход.
и шероховатости, то наивыгоднейшим из них будет то сечение, которое при том же уклоне будет пропускать наибольший расход.
Рассматривая формулу расхода  , следует отметить, что при постоянных площади сечения
, следует отметить, что при постоянных площади сечения  и уклоне
и уклоне 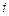 расход
расход  тем больше, чем больше гидравлический радиус
тем больше, чем больше гидравлический радиус 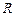 . Но так как
. Но так как 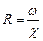 , то максимальной пропускной способностью будет обладать сечение с наименьшим смоченным периметром
, то максимальной пропускной способностью будет обладать сечение с наименьшим смоченным периметром  .
.
Таким образом, вопрос сводится к нахождению формы сечения с минимальной величиной смоченного периметра  при заданной площади сечения
при заданной площади сечения  .
.
В трапецеидальном сечении при одинаковой площади живого сечения  и постоянном коэффициенте заложения откоса
и постоянном коэффициенте заложения откоса  , назначаемом в зависимости от рода грунта, может быть различное соотношение между шириной по дну
, назначаемом в зависимости от рода грунта, может быть различное соотношение между шириной по дну 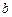 и глубиной
и глубиной 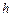 .
.
Наивыгоднейшей с гидравлической точки зрения будет такая форма трапеции, которая при одинаковой площади живого сечения  обладает наименьшим смоченным периметром
обладает наименьшим смоченным периметром  .
.
Найдем такое отношение ширины дна к глубине 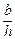 , которое дает минимальный смоченный периметр. Для этого исследуем на минимум функцию
, которое дает минимальный смоченный периметр. Для этого исследуем на минимум функцию  при постоянной площади сечения
при постоянной площади сечения  и постоянном коэффициенте заложения откоса
и постоянном коэффициенте заложения откоса  .
.
Выразив ширину канала по дну 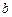 из формулы (7.12) и подставив это значение в формулу (7.14), получим следующее соотношение:
из формулы (7.12) и подставив это значение в формулу (7.14), получим следующее соотношение:
 . (7.18)
. (7.18)
Найдем производную смоченного периметра по глубине;
 .(7.19)
.(7.19)
При минимуме  производная
производная 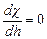 и тогда, соответственно, приняв отношение
и тогда, соответственно, приняв отношение  получим выражение, определяющее соотношение между шириной
получим выражение, определяющее соотношение между шириной 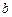 и глубиной
и глубиной 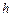 для гидравлически наивыгоднейшего сечения трапецеидальной формы:
для гидравлически наивыгоднейшего сечения трапецеидальной формы:
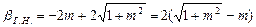 . (7.20)
. (7.20)
Следует отметить еще свойство гидравлически наивыгоднейшего трапецеидального сечения. Если в выражении для гидравлического радиуса (7.15) заменить 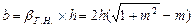 , то после сокращения имеем
, то после сокращения имеем
 , (7.21)
, (7.21)
т.е. для трапецеидальных гидравлически наивыгоднейших сечений гидравлический радиус 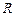 равен половине глубины.
равен половине глубины.
При различных значениях коэффициента  из всех трапеций наивыгоднейшей будет та, которая представляет собой половину правильного шестиугольника, т.е. при
из всех трапеций наивыгоднейшей будет та, которая представляет собой половину правильного шестиугольника, т.е. при 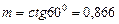 .
.
Дата добавления: 2015-04-29; просмотров: 2247;
