ГИБКОСТЬ ЭЛЕМЕНТОВ

4.3. Гибкость элемента 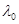принимается:

а) для элементов сплошного сечения – в обеих плоскостях, а для составных элементов – при изгибе в плоскости, нормальной к плоскости соединительных планок, перфорированных листов или соединительной решетки, по формуле

,

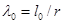где l₀ – свободная длина элемента, см; r – радиус инерции сечения элемента относительно оси, перпендикулярной плоскости изгиба, см;

б) для составных элементов в случае изгиба в плоскости параллельной перфорированным листам, соединительной решетке или соединительным планкам, равной приведенной гибкости 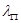, определяемой по формулам:

при соединительных планках или перфорированных листах

;

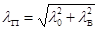при соединительной решетке

,

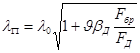но не менее

;

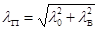где 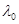- гибкость всего элемента в плоскости соединительных планок, перфорированных листов или соединительной решетки (как сплошного сечения); 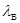- гибкость ветви (за свободную длину ветви l_В принимается расстояние между крайними заклепками соединительных планок, расстояние в свету между приваренными планками, 80% длины отверстия в перфорированном листе или длина панели соединительной решетки); радиус инерции ветви определяется относительно оси перпендикулярной плоскости планок или решетки; F_бр – площадь брутто поперечного сечения всего элемента, см²; F_Д – площадь брутто поперечного сечения всех диагоналей соединительной решетки, попадающих в один поперечный разрез элемента, см²; 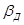- коэффициент, отражающий влияние жесткости диагоналей соединительной решетки: для диагоналей из уголков, а также диагоналей из уголков и полос (крестовая решетка) 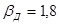; для диагоналей из полос 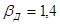; 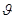- коэффициент, зависящий от гибкости элемента.

Для элементов с гибкостью 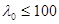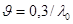; при .

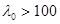
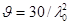Гибкость любого элемента, работающего на растяжение или сжатие, следует определять с учетом всех частей сечения. Например, при подсчете площади, момента инерции и радиуса инерции поперечного сечения элемента учитывается эквивалентная толщина перфорированных листов или соединительных планок 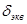, определяемая следующим образом:

для перфорированных листов шириной a_Л, длиной l_Л и толщиной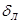

,

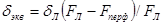где F_Л=a_Лl_Л – площадь листа без учета перфорации, см²; F_перф – площадь перфорации, см²;

для соединительных планок толщиной 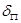и длиной l_ПЛ

,

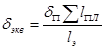где 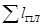- суммарная длина планок по длине элемента, м; l_э – геометрическая длина элемента, м.

СВОБОДНЫЕ ДЛИНЫ ЭЛЕМЕНТОВ

4.4. Свободная длина элемента пояса в плоскости фермы принимается равной расстоянию между центрами смежных узлов фермы; из плоскости фермы (при наличии связей в плоскости рассматриваемых поясов) свободная длина элемента пояса равна панели связей.

4.5. Свободная длина опорных раскосов и стоек определяется, как для элементов поясов (см. п. 4.4). Для частей опорных раскосов и стоек, входящих в состав портальных рам, свободная длина из плоскости фермы определяется в соответствии с указаниями п. 5.3.

Свободная длина других элементов решетки ферм с треугольной, раскосной и полураскосной решетками принимается равной:

в плоскости ферм – расстоянию между центрами прикрепления элемента к фасонкам или к поясам;

из плоскости ферм – расстоянию между центрами узлов элемента или наибольшей части этого расстояния, если полная длина элемента разделена поперечными связями. Для стойки полураскосной фермы, если нет поперечных связей, 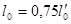( 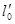- длина элемента между центрами смежных узлов, см).

Свободная длина элементов решетки многорешетчатых и многораскосных ферм принимается равной:

при изгибе в плоскости ферм – расстоянию между центрами пересечений или расстоянию между центром прикрепления к поясу и центром ближайшего пересечения;

при изгибе из плоскости фермы

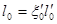. (4.6)

Коэффициент 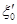находят по графику (приложение 17) в зависимости от числа пересечений и жесткости элементов EI, с которыми пересекается данный элемент. Если жесткость встречного растянутого элемента равна 0,75 и более жесткости рассчитываемого сжатого элемента, то следует пользоваться графиком для пересечений с жесткими элементами; в остальных случаях – графиком для пересечений с плоскими элементами. Если встречный растянутый жесткий элемент в месте пересечения перекрыт накладкой, имеющей жесткость менее 0,75 жесткости рассчитываемого сжатого элемента, то пересечение с таким элементом учитывается, как с плоским.

Пересечения сжатого стержня со сжатым, а также примыкание нерабочего элемента к сжатому элементу уменьшает свободную длину только в плоскости фермы.

Для элементов решетки двух – и многораскосных систем с двухступенчатыми поясами, стойки которых имеют соединительную решетку, раскосы ее не имеют, за длину раскоса 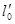принимается часть его, расположенная между стойками или между стойкой и поясом. При определении свободной длины жесткой стойки с соединительной решеткой пересечения ее с гибкими элементами, не имеющими соединительной решетки, не учитываются.

Свободная длина элемента, определяемая по формуле (4.6), не должна приниматься меньше его свободной длины при изгибе в плоскости фермы.

Для многорешетчатых ферм с плоскими раскосами и со стойками жескости коэффициент 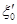находят по графику приложения 18 в зависимости от отношения расчетной высоты фермы к расстоянию между стойками жесткости, независимо от того, были ли поставлены стойки жесткости при сборке или при усилении пролетного строения.

4.6. Свободная длина сжатого пояса фермы (балки) в пролетном строении открытого типа из плоскости фермы

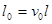, (4.7)

где l – расчетный пролет фермы (балки), см; v0– коэффициент (табл. 4.1), зависящий от параметра :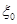

,

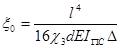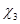- коэффициент размерности, равный 0,01 при расчетах в системе СИ или 1,0 – в СГС; d – длина панели, см; E – модуль упругости, МПа (тс/см2), см. п.2.1; IПС– момент инерции сжатого пояса (среднее значение по длине) относительно вертикальной оси, см4; 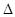- наибольшее горизонтальное перемещение оси, см, верхнего узла неопорной наиболее гибкой полупамы от горизонтальной силы P=1,0 кН (тс), приложенной в этом узле:

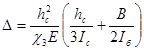; (4.8)

hc– высота стойки (или ребра жесткости), равная расстоянию от центра тяжести сечения сжатого пояса до верха поперечной балки, см; B – расстояние между осями главных ферм (балок), см; Ic– момент инерции сечения стойки (ребра жесткости), соответствующий изгибу из плоскости фермы (среднее значение по высоте), см4; Iб– момент инерции сечения поперечной балки, см4.

Таблица 4.1. Коэффициенты v0

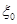
	0	1	5	10	15	30	60
v0	0,696	0,662	0,524	0,433	0,396	0,353	0,321
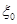
						1000 и более
v0	0,290	0,268	0,246	0,225	0,204	0,174
Примечание. При промежуточных значениях 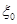коэффициент v0определяется по интерполяции.

 

Коэффициенты v0в зависимости от 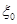для ферм (балок) с параллельными поясами приведены в табл. 4.1.

При полигональном очертании верхнего пояса v0допускается принимать по табл. 4.1. В этом случае, параметр 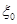нужно определять для полурамы, расположенной посередине пролета, а вместо расчетного пролета фермы (балки) l принимать полную длину сжатого пояса.

4.7. Свободная длина стоек пролетного строения открытого типа l0при изгибе в плоскости фермы равна геометрической длине стойки, а при изгибе из плоскости фермы – удвоенной ее длине.