Деформации и напряжения

Напряжение – мера внутренних сил, возникающих в материале под влиянием внешних воздействий (нагрузок, изменения температуры и пр.). Для изучения напряжений через произвольную точку тела мысленно проводится сечение (рис. 3.1) и отбрасывается одна из половин тела. Действие отброшенной половины на другую половину заменяют внутренними силами.

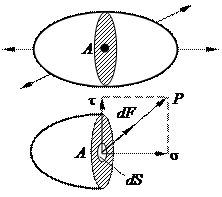
Рис. 3.1. Схема замены внешних сил на внутренние напряжения

В малом элементе сечения площадью dS в окрестности произвольной точки А действует произвольно направленная внутренняя сила dF.
Отношение р = dF/dS называется вектором напряжения в точке А по площадке dS. Составляющие вектора напряжения, действующие по нормали к площадке, обозначаются σ и называются нормальными напряжениями, а действующие вдоль площадки называются касательными напряжениями τ в точке А по площадке dS, причём σ² + τ² = р².

В общем случае напряженное состояние тела в точке А характеризуется совокупностью всех векторов напряжений для всевозможных сечений (площадок, проходящих через точку А), а значит и для любого направления. Напряженное состояние в точке А может быть определено с помощью тензора напряжений и характеризуется девятью компонентами по трем осям координат (три нормальных и шесть касательных). Касательные напряжения попарно равны (τ_ху = τ_ух, τ_хz = τ_zх, τ_уz = τ_zу), т. е. остается всего шесть компонентов. Напряжения выражаются в Па (паскалях).

Т_н = 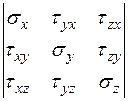. (3.1)

Для тензора характерным является закон, по которому преобразуется его компоненты при повороте осей координат. При повороте системы координат можно отыскать такое ее положение, когда касательные напряжения будут равны нулю. Эти направления называют главными.

Главные направления тензора напряжений определяются условием, зависящим от трех инвариантов I₁, I₂, I₃ .

Первым инвариантом I₁ тензора напряжений является сумма нормальных напряжений:

I₁ = σ_х + σ_у + σ_z = 3σ₀. (3.2)

Среднее значение трёх нормальных напряжений называют гидростатическим давлением:

σ₀ = (σ_х + σ_у + σ_z)/3. (3.3)

Гидростатическому давлению соответствует тензор напряжений, нормальные компоненты которого равны σ₀, а касательные – нулю. Поскольку гидростатическое давление не вызывает в металле пластических деформаций, его исключают из системы напряжений. Оставшуюся часть тензора называют девиатором напряжений S_σ:

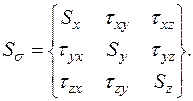(3.4)

Второй инвариант I₂ тензора напряжений определяется следующим выражением:

I₂ = σ_х σ_у + σ_х σ_z + σ_уσ_z – τ²_ху – τ²_уz – τ²_zх. (3.5)

Величины, пропорциональные корню квадратному из второго инварианта девиатора напряжений, называют интенсивностью касательных напряжений τ_i и интенсивностью нормальных напряжений σ_i:

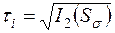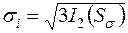, . (3.6)

Напряжения в материале могут возникнуть при физико-химических процессах, при неравномерном распределении температуры (при нагреве и охлаждении металла), а также вследствие фазовых превращений при термической обработке. При этом напряжения, возникающие в объеме всего тела, называют макронапряжениями (или напряжениями Ι рода), а напряжения, возникающие в объеме одного зерна, называют микронапряжениями (или напряжениями ΙΙ рода). Напряжения, возникающие в объемах порядка нескольких параметров кристаллической решетки, называются субмикроскопическими (или напряжениями ΙΙΙ рода). Деформациями называют изменения формы или размеров тела (или части тела) под действием внешних сил, а также при нагревании или охлаждении и других воздействиях, вызывающих изменение относительного положения частиц тела (рис. 3.2).

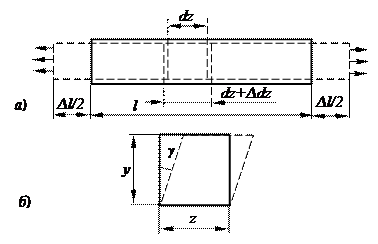
Рис. 3.2. Схема деформации: а) линейная деформация, б) угловая деформация

С геометрической точки зрения деформированное состояние в точке описывается тензором деформации:

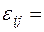
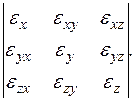(3.7)

Компоненты , характеризуют линейные деформации волокон, расположенных по осям x, y, z: относительные удлинения (или относительные укорочения), а компоненты 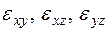– углы поворота двух взаимно перпендикулярных до деформации волокон (или деформации сдвига).

Для компонент деформаций сдвига справедливы равенства:

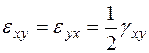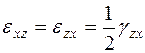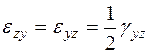, , . (3.8)

При повороте системы координат все компоненты тензора деформации преобразуются по определенным линейным относительно направляющих косинусов соотношениям. В теории деформации и линейных преобразований доказывается, что из всех возможных направлений осей координат существует тройка взаимно перпендикулярных направлений (главных направлений), относительно которых все сдвиговые компоненты деформации равны нулю. Главные направления деформаций определяются тремя скалярными величинами, не зависящими от положения системы координат и поэтому называемыми инвариантами.

Первый инвариант 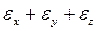используется для записи условия постоянства объема деформируемого металла:

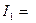
= 0. (3.9)

Второй инвариант тензора деформации имеет вид:

I₂ = 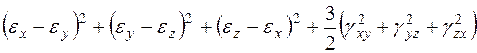. (3.10)

Величина, пропорциональная корню квадратному из второго инварианта, называется интенсивностью деформаций и используется для характеристики деформаций в общем случае деформированного состояния.

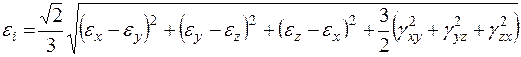. (3.11)

Простейшие схемы деформирования – растяжение, сжатие, сдвиг, кручение, изгиб. Первые две схемы (растяжение и сжатие) могут быть описаны только линейными компонентами, вторые (сдвиг, кручение, изгиб) – только сдвиговыми (угловыми).