Коэффициентом отражения

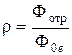(2.6)

и коэффициентом поглощения

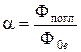, (2.7)

где 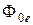– поток (мощность) падающего излучения; Ф_пр – поток прошедшего излучения; Ф_отр – поток отражённого излучения; Ф_погл – поток поглощённого излучения.

Коэффициенты t, r и a зависят от свойств самого тела и длины волны падающего излучения. Спектральная зависимость, т.е. зависимость коэффициентов от длины волны, определяет цвет как прозрачных, так и непрозрачных (t= 0) тел.

Согласно закону сохранения энергии

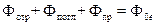. (2.8)

Разделив обе части равенства (2.8) на 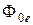, получим:

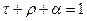(2.9)

Тело, для которого 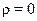, , 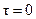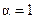называется абсолютно чёрным.

Абсолютно чёрное тело – это тело, которое при любой не разрушающей его температуре полностью поглощает всю энергию падающего на него излучения любой длины волны. Все реальные тела не являются абсолютно чёрными. Однако некоторые из них в определенных интервалах длин волн близки по своим свойствам к абсолютно чёрному телу. Например, в области длин волн видимого света коэффициенты поглощения сажи, платиновой черни и черного бархата мало отличаются от единицы.

Наиболее совершенной моделью абсолютно чёрного тела может служить малое отверстие в замкнутой полости сферической формы. Свет, попадающий через отверстие внутрь полости, будет многократно отражаться от стенок, прежде чем сможет выйти наружу. При каждом отражении свет, независимо от материала стенок, частично поглощается. В результате многократных отражений внутри полости излучение будет практически полностью поглощено, и отверстие снаружи кажется совершенно чёрным. Очевидно, что эта модель тем ближе по характеристикам к чёрному телу, чем больше отношение площади поверхности полости к площади отверстия (рис. 2.1).

Рис. 2.1. Модель абсолютно чёрного тела

Каждое тело может не только испускать, но и поглощать тепловое излучение. Опыты показывают, что чем больше энергии тело излучает при некоторой постоянной температуре, тем сильнее оно поглощает излучение такого же спектрального состава при той же температуре.

Спектральной характеристикой поглощения электромагнитных волн телом является спектральный коэффициент поглощения 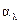– величина, определяемая отношением поглощённого телом потока излучения в малом спектральном интервале (от 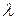до 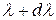) к потоку падающего на него излучения в том же спектральном интервале

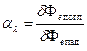. (2.10)

В 1859 г. немецкий физик Густав Кирхгоф (1824-1887гг.) на основании второго начала термодинамики установил один из основных законов теплового излучения.

Закон Кирхгофа: отношение спектральной плотности энергетической светимости равно­весного излучения тела к его спектральному коэффициенту поглощения не зависит от природы тела; для всех тел оно является универсальной функцией длины волны излучения и температуры тела

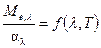. (2.11)

Закон Кирхгофа был подтвержден опытным путём.

Для абсолютно чёрного тела 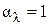. Поэтому из закона Кирхгофа следует, что

,

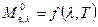где 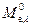– спектральная плотность энергетической светимости абсолютно чёрного тела.

Таким образом, универсальная функция Кирхгофа 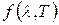представляет собой спектральную плотность энергетической светимости абсолютно чёрного тела. Поэтому выражение закона Кирхгофа (2.11) можно записать в виде

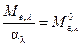. (2.12)

Из формулы (2.12) следует, что:

1) для всех тел отношение спектральной плотности энергетической светимости к спектральному коэффициенту поглощения равно спектральной плотности энергетической светимости абсолютно чёрного тела при тех же значениях 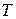и ;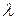

2) спектральная плотность энергетической светимости любого тела в любой области спектра всегда меньше спектральной плотности энергетической светимости абсолютно чёрного тела (при одних и тех же значениях длины волны и температуры);

3) если тело при некоторой температуре не поглощает электромагнитные волны в интервале длин от 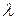до 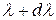, то оно их в этом интервале длин при данной температуре и не излучает;

4) тело, которое при данной температуре сильнее поглощает, должно интенсивнее излучать. Например, при накаливании платиновой пластинки, часть которой покрыта платиновой чернью, её зачернённый конец светится значительно ярче, чем светлый.

Аналитический вид функции 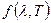для абсолютно черного тела
был установлен учеником Кирхгофа Максом Планком на основе квантовых представлений о природе излучения.

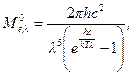(2.13)

где 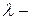длина волны излучения; 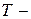температура излучающего тела; 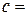3×10⁸ 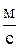– скорость света в вакууме; k = 1,38×10^-23 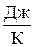– постоянная Больцмана; 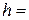6,63×10^-34 Дж×с – постоянная Планка.

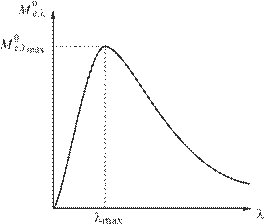
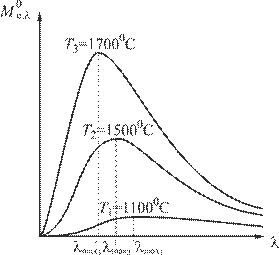
Спектр излучения абсолютно черного тела имеет характерный максимум (рис. 2.2), который при повышении температуры сдвигается в коротковолновую часть (рис. 2.3).

Рис. 2.2. Кривая распределения энергии в спектре абсолютно чёрного тела	Рис. 2.3. Кривые спектральной плотности энергетической светимости при различной температуре излучающего тела

Положение максимума спектральной плотноcти энергетической светимости можно определить из выражения (2.13) обычным способом, приравняв к нулю первую производную:

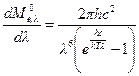
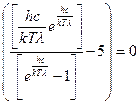. (2.14)

Обозначив 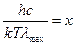, получим:

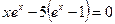. (2.15)

Решение этого трансцендентного уравнения численным методом дает значение 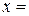4,965.

Следовательно,

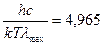, (2.16)

откуда

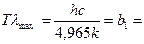2,898· 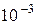м·K, (2.17)

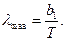(2.18)

где 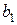– первая постоянная Вина.

Таким образом, функция 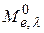достигает максимума при длине волны, обратно пропорциональной термодинамической температуре абсолютно чёрного тела.

Эта зависимость была установлена в 1893 г. немецким физиком Вильгельмом Вином(1864-1928гг.)на основе законовклассической термодинамики и электромагнитной теории света. Её называют законом смещения Вина, подчёркивая тем самым, что с ростом температуры максимум спектральной плотности энергетической светимости сдвигается в сторону меньших длин волн (больших частот).

Из закона Вина следует, что при низких температурах излучаются преимущественно длинные (инфракрасные) электромагнитные волны. По мере же возрастания температуры увеличивается доля излучения, приходящаяся на видимую область спектра, и тело начинает светиться. С дальнейшим ростом температуры яркость свечения увеличивается, а цвет изменяется. Поэтому цвет излучения может служить характеристикой температуры излучения. Примерная зависимость цвета свечения тела от его температуры приведена в табл. 2.1.

Таблица 2.1

Подставив формулу (2.18) в выражение (2.13), Вин показал, что максимальное значение функции 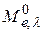пропорционально пятой степени термодинами­ческой температуры тела. Это утверждение носит название второго закона Вина. Он был получен в 1896 году.

Математическое выражение второго закона Вина имеет вид

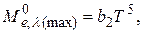(2.19)

где 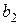– вторая постоянная Вина ( · ).

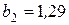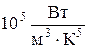В 1911 г. Вильгельм Винбыл удостоен Нобелевской премии по физике за работы по тепловому излучению.

Энергетическую светимость абсолютно чёрного тела можно найти из выражения (2.13) простым интегрированием по длине волны

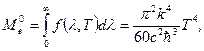(2.20)

где 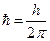– приведённая постоянная Планка,

или

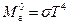(2.21)

где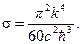

Энергетическая светимость абсолютно чёрного тела пропорциональна четвёртой степени его термодинамической температуры.

Это положение носит название закона Стефана – Больцмана по имени австрийских физиков Йозефа Стефана (1835-1893гг.) и Людвига Больцмана (1844-1906гг.).

Коэффициент пропор­циональности 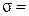5,67×10^-8 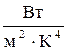называется постоянной Стефана – Больцмана.

Абсолютно чёрное тело является идеализацией реальных тел. Реальные тела испускают излучение, спектр которого не описывается формулой Планка. Их энергетическая светимость, кроме температуры, зависит от природы тела и состояния его поверхности. Эти факторы можно учесть, если в формулу (2.21) ввести коэффициент 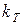, показывающий, во сколько раз энергетическая свети­мость абсолютно чёрного тела при данной температуре больше энер­гетической светимости реального тела при той же температуре

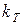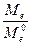= , (2.22)

откуда ,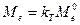

или 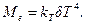(2.23)

Для всех реальных тел 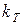<1 и зависит как от природы тела и состояния его поверхности, так и от температуры. В частности, для вольфрамовых нитей электроламп накаливания зависимость 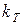от 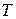имеет вид, представленный на рис. 2.4.

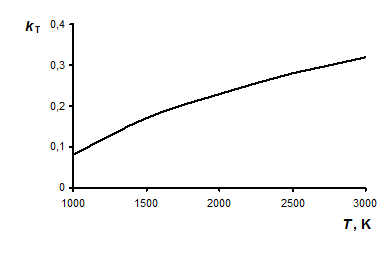
Рис. 2.4. Зависимость 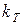от температуры 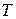тела