Последовательностей.

Пусть имеем участок цепи на рис. 6. Для фазы А этого участка можно записать

.

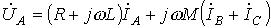(9)

Тогда для симметричных составляющих прямой и обратной последовательностей с учетом, того, что 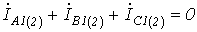, на основании (9) имеем

.

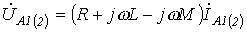Отсюда комплексные сопротивления прямой и обратной последовательностей одинаковы и равны:

.

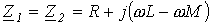Для симметричных составляющих нулевой последовательности с учетом равенства 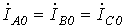соотношение (9) трансформируется в уравнение

,

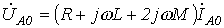откуда комплексное сопротивление нулевой последовательности

.

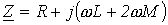В рассмотренном примере получено равенство сопротивлений прямой и обратной последовательностей. В общем случае эти сопротивления могут отличаться друг от друга. Наиболее типичный пример – различие сопротивлений вращающейся машины для токов прямой и обратной последовательностей за счет многократной разницы в скольжении ротора относительно вращающегося магнитного поля для этих последовательностей.