Цикл Карно.
 |
Анализируя работу тепловых двигателей, Карно пришел к выводу, что наивыгоднейшим процессом является обратимый круговой процесс, состоящий из двух изотерм и двух адиабат, так как он характеризуется наибольшим коэффициентом полезного действия. Такой цикл получил название цикла Карно.
Цикл Карно – прямой круговой процесс, при котором выполненная системой работа максимальна.
Пусть некоторая система может вступать в тепловой контакт с двумя тепловыми резервуарами, температуры которых Т1 и Т2, а теплоемкости бесконечно велики (то есть добавление или отнятие некоторого количество теплоты не изменяет температуры). Примем, что система представляет собой идеальный газ, находящийся в цилиндрическом сосуде под поршнем (рис. 8.7.). Считаем, что стенки и поршень теплонепроницаемы.
Пусть сначала система, находящаяся в состоянии с (р1, V1, Т1), приводится в тепловой контакт с первым резервуаром. При сообщении системе теплоты Q1 совершается работа против внешних сил, численно равная Q1, газ расширяется до объема V2.
Затем цилиндр переставляется на изолирующую подставку. Газу предоставляется возможность и дальше расширяться до объема V3, чтобы температура стала Т2.
Переведем цилиндр с поршнем в тепловой контакт со вторым резервуаром с температурой Т2, причем внешние тела совершают работу Q2 над системой, так что объем становится V4.
Вновь изолируем систему и уменьшаем объем до первоначального значения V1, так что температура повысится от Т2 до Т1.
Если все четыре процесса являются обратимыми, то все наши рассуждения справедливы, и система действительно вернется в исходное состояние с (р1, V1, Т1).
Итак, описанный цикл состоит из двух изотермических (1®2 и 3®4) и двух адиабатических расширений и сжатий (2®3 и 4®1) (см. рис.8.8.). Машина, совершающая цикл Карно, называется идеальной тепловой машиной.
 |
Работа, совершаемая при изотермическом расширении:
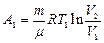 ; А1=Q1. (8.8.1)
; А1=Q1. (8.8.1)
При адиабатическом расширении работа совершается за счет убыли внутренней энергии системы, т.к. Q’=0: 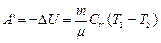
Работа, совершаемая над системой при изотермическом сжатии:
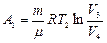 ; А2=Q2. (8.8.2)
; А2=Q2. (8.8.2)
Работа при адиабатическом сжатии: А'' =–DU = 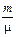 СV(Т2–Т1).
СV(Т2–Т1).
Подсчитаем КПД идеальной тепловой машины.
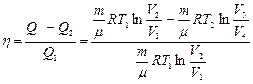 (8.8.3)
(8.8.3)
Запишем уравнения Пуассона для двух адиабатических процессов:
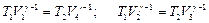
Взяв их отношение, получим: 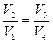 . Выразив в формуле (8.8.3)
. Выразив в формуле (8.8.3) 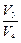 через
через 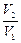 и сократив на ln
и сократив на ln 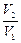 , получим:
, получим:
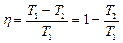 . (8.8.4)
. (8.8.4)
Отсюда сформулируем первую теорему Карно: коэффициент полезного действия обратимого цикла Карно не зависит от природы рабочего тела и является функцией только абсолютных температур нагревателя и холодильника.
Вторая теорема Карно: любая тепловая машина, работающая при данных значениях температур нагревателя и холодильника, не может иметь большего КПД, чем машина, работающая по обратимому циклу Карно при тех же значениях температур нагревателя и холодильника.
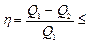
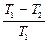 .
.
Термический КПД произвольного обратимого цикла
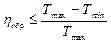 ,
,
где Тmax и Tmin – экстремальные значения температуры нагревателя и холодильника, участвующих в осуществлении рассматриваемого цикла.
Дата добавления: 2015-04-19; просмотров: 1280;
