Измерение горизонтальных углов в теодолитном ходе

Измерения угла выполняется строго по методике, соответствующей способу измерения; известно несколько способов измерения горизонтальных углов: это способ отдельного угла (способ приемов), способ круговых приемов, способ во всех комбинациях и др.

Способ отдельного угла. Измерение отдельного угла складывается из следующих действий:

наведение трубы на точку, фиксирующую направление первой стороны угла (рис.4.16), при круге лево (КЛ), взятие отсчета L₁;

поворот алидады по ходу часовой стрелки и наведение трубы на точку, фиксирующую направление второй стороны угла; взятие отсчета L₂,

вычисление угла при КЛ (рис.4.16):

β_л = L₂ - L₁,

перестановка лимпба на 1^o - 2^o для теодолитов с односторонним отсчитыванием и на 90^o - для теодолитов с двухсторонним отсчитыванием,

переведение трубы через зенит и наведение ее на точку, фиксирующую направление первой стороны угла, при круге право (КП); взятие отсчета R₁,

поворот алидады по ходу часовой стрелки и наведение трубы на точку, фиксирующую направление второй стороны угла; взятие отсчета R₂,

вычисление угла при КП:

β_п = R₂ - R₁,

при выполнении условия |β_л - β_п| < 1.5 * t, где t - точность теодолита, вычисление среднего значения угла:

β_ср = 0.5 * (β_л + β_п).

Измерение угла при одном положении круга (КЛ или КП) составляет один полуприем; полный цикл измерения угла при двух положениях круга составляет один прием.

Запись отсчетов по лимбу и вычисление угла производятся в журналах установленной формы.

Способ круговых приемов. Если с одного пункта наблюдается более двух направлений, то часто применяют способ круговых приемов. Для измерения углов этим способом необходимо выполнить следующие операции (рис.4.17):

при КЛ установить на лимбе отсчет, близкий к нулю, и навести трубу на первый пункт; взять отсчет по лимбу.

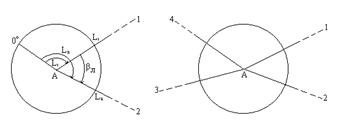
Рис.4.16 Рис.4.17

вращая алидаду по ходу часовой стрелки, навести трубу последовательно на второй, третий и т.д. пункты и затем снова на первый пункт; каждый раз взять отсчеты по лимбу.

перевести трубу через зенит и при КП навести ее на первый пункт; взять отсчет по лимбу.

вращая алидаду против хода часовой стрелки, навести трубу последовательно на (n-1), ..., третий, второй пункты и снова на первый пункт; каждый раз взять отсчеты по лимбу.

Затем для каждого направления вычисляют средние из отсчетов при КЛ и КП и после этого - значения углов относительно первого (начального) направления.

Способ круговых приемов позволяет ослабить влияние ошибок, действующих пропорционально времени, так как средние отсчеты для всех направлений относятся к одному физическому моменту времени.

Влияние внецентренности теодолита на отсчеты по лимбу. Пусть на рис.4.18 ось вращения алидады пересекает горизонтальную плоскость в точке B', а точка B - проекция вершины измерямого угла на ту же плоскость. Расстояние между точками B и B' обозначим l, расстояние между пунктами B и A - S.

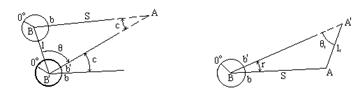
Рис.4.18 Рис.4.19

Если бы теодолит стоял в точке B, то при наведении трубы на точку A отсчет по лимбу был бы равен b. Перенесем теодолит в точку B', сохранив ориентировку лимба; при этом отсчет по лимбу при наведении трубы на точку A изменится и станет равным b'; различие этих отсчетов называется ошибкой центрировки теодолита и обозначается буквой c.

Из треугольника BB'A имеем:

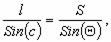
откуда

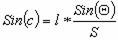
или по малости угла c

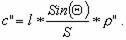(4.18)

Величина l называется линейным элементом центрировки, а угол Q - угловым элементом цетрировки; угол Q строится при проекции оси вращения теодолита и отсчитывается от линейного элемента по ходу часовой стрелки до направления на наблюдаемый пункт A.

Правильный отсчет по лимбу будет:

b = b' + c . (4.19)

Влияние редукции визирной цели на отсчеты по лимбу.

Если проекция визирной цели A' на горизонтальную плоскость не совпадает с проекцией центра наблюдаемого пункта A, то возникает ошибка редукции визирной цели (рис.4.19). Отрезок AA' называется линейным элементом редукции и обозначается l₁; угол Q1 называется угловым элементом редукции; он строится при проекции визирной цели и отсчитывается от линейного элемента по ходу часовой стрелки до направления на пункт установки теодолита. Обозначим правильный отсчет по лимбу - b, фактический - b', ошибка в направлении BA равна r. Из треугольника BAA' можно написать:

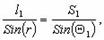
откуда

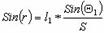
или по малости угла r

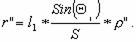(4.20)

Правильный отсчет по лимбу будет

b = b' + r . (4.21)

Наибольшего значения поправки c и r достигают при Θ = Θ₁ = 90^o ( 270^o ), когда .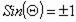

В этом случае

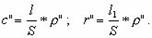
В практике измерения углов применяют два способа учета внецентренности теодолита и визирной цели.

Первый способ заключается в том, что центрирование выполняют с такой точностью, которая позволяет не учитывать ошибку внецентренности. Например, при работе с техническими теодолитами допустимое влияние ошибок центрирования теодолита и визирной цели можно принять c = r = 10"; при среднем расстоянии между точками S = 150 м получается, что l = l₁ = 0.9 см, то-есть, теодолит или визирную цель достаточно устанавливать над центром пункта с ошибкой около 1 см. Для центрирования с такой точностью можно применить обычный отвес.

Центрирование теодолита или визирной цели с точностью 1-2 мм можно выполнить лишь с помощью оптического центрира.

Второй способ заключается в непосредственном измерении элементов l и Θ, l₁ и Θ₁, вычислении поправок c и r по формулам (4.18) и (4.20) и исправлении результатов измерений этими поправками по формулам (4.19) и (4.21).