Распределение энергии по степеням свободы молекул

Термодинамика – наука о наиболее общих свойствах физических макросистем, находящихся в состоянии термодинамического равновесия, и о процессах перехода между этими состояниями. Термодинамика построена на основе фундаментальных начал (законов), которые являются обобщением большого числа наблюдений и выполняются независимо от конкретной природы тел, образующих систему. Однако рассматривая основные понятия термодинамики, мы будем использовать и статистическую интерпретацию.

Основными понятиями термодинамики являются такие понятия как состояние, процесс, цикл, внутренняя энергия, работа, количество теплоты, теплоёмкость, энтропия, свободная энергия, энтальпия, функция Гиббса.

Среднюю кинетическую энергию движения молекулы идеального газа можно определить по формуле:

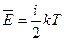(9-1)

Число степеней свободыi определяется числом независимых координат и осей, описывающих движение частицы в пространстве. На каждую степень свободы статистической системы приходится одна и та же энергия, равная 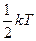. В этом состоит суть теоремы о равнораспределении тепловой энергии по степеням свободы. Для сложных молекул, состоящих из нескольких атомов, число степеней свободы увеличивается за счёт вращательных и колебательных. Если пренебречь изменением потенциальной энергии взаимодействия частиц, то молекулы можно рассматривать как «жёсткие». Для жестких двухатомных молекул число степеней свободы i равно 5 , из них 3 – поступательных ( три независимые координаты х,y,z, описывающие положение частицы в пространстве) и 2 вращательных. (две независимых оси вращения). Для жёстких трёхатомных и многоатомных молекул число степеней свободы равно 6, из них 3 поступательных и 3 вращательных. Для жёстких одноатомных молекул число степеней свободы равно 3 и все они поступательные.

Энергия – величина аддитивная. Поэтому среднюю кинетическую энергию одного моля молекул можно определить, усреднив энергии всех частиц одного моля: 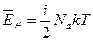, где 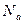- число молекул в одном моле вещества (число Авогадро). Учитывая, что произведение числа Авогадро и постоянной Больцмана равно универсальной газовой постоянной, получим энергию одного моля молекул :

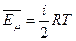(9-2)

Среднюю кинетическую энергию любого количества идеального газа можно определить, усреднив энергии всех рассматриваемых частиц. Учитывая, что количество молекул в одном моле вещества очень велико, следовательно, средние кинетические энергии разных молей молекул практически одинаковы. Тогда средняя кинетическая энергия любого количества вещества может быть определена по формуле:

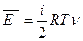(9-3)