Основные свойства газовых смесей

В технике очень часто приходится иметь дело с газообразными веществами, представляющими механическую смесь отдельных газов, например, доменный и светильный газ, отходящие газы из котельных установок, двигателей внутреннего сгорания, реактивных двигателей и других тепловых установок. Воздух также представляет собой газовую смесь, состоящую из азота, кислорода, углекислого газа, водяных паров и одноатомных газов. Поэтому для решения практических задач необходимо уметь определять основные параметры газовой смеси: газовую постоянную, среднюю молекулярную массу, парциальные давления и др.

Под газовой смесью понимается механическая смесь отдельных газов, не вступающих между собой ни в какие химические реакции. Каждый газ в смеси, независимо от других газов, полностью сохраняет все свои свойства и ведет себя так, как если бы он один занимал весь объем смеси. Молекулы газа создают давление на стенки сосуда, которое называется парциальным (частичным). Будем считать, что каждый отдельный газ, входящий в смесь, подчиняется уравнению состояния Клапейрона, т. е. является идеальным газом.

Газовая смесь идеальных газов подчиняется закону Дальтона, который гласит: общее давление смеси газов равно сумме парциальных давлений отдельных газов, составляющих смесь:

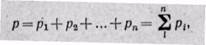(3-1)

где p₁, р₂, ..., р_п — парциальные давления.

Парциальным давлением называют такое, которое имел бы каждый газ, входящий в состав смеси, если бы этот газ находился один в том же количестве, в том же объеме и при той же температуре, что и в смеси.

Параметры газовой смеси могут быть вычислены по уравнению Клапейрона

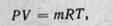
где все величины, входящие в уравнение относятся к смеси газов.

Таким образом, задачей расчета газовой смеси является определение на основании заданного состава смеси средней молекулярной массы, или газовой постоянной, смеси газов, после чего получение всех остальных параметров можно произвести по уравнению состояния для смеси.

Дополнительно часто требуется также определение и парциальных давлений газов, входящих в смесь.

При дальнейшем изложении этой главы все величины без значков будем относить к газовым смесям, а величины со значками — к отдельным газам.

Способы задания смеси газов. Газовая смесь может быть задана массовыми, объемными и мольными долями.

Массовой долей называют отношение массы каждого газа к общей массе смеси:

где g₁, g₂.....g_n—массовые доли;

m₁, m₂,..., т_n—масса каждого газа;

т—масса всей смеси. Сумма массовых долей равна единице:

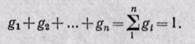
Сумма масс всех газов равна массе смеси:

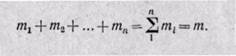
Объемной долейназывают отношение парциального (приведенного) объема каждого газа к общему объему смеси газов:

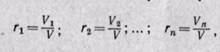
где r₁, r₂,...,r_n— объемные доли; V₁, V₂,..., V_n—парциальные (приведенные) объемы

каждого газа; V — объем смеси газов.

Парциальным объемом газа называют объем, который занимал бы этот газ, если бы его температура и давление равнялись температуре и давлению смеси газов.

Парциальный объем каждого газа можно определить по закону Бойля — Мариотта. При постоянной температуре имеем

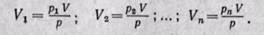
Сложив полученные уравнения, будем иметь

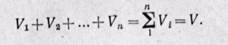
Сумма парциальных объемов газов, составляющих смесь, равна объему смеси газов.

Сумма объемных долей равна единице:

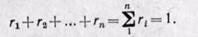
Задание смеси мольными долями равнозначно заданию ее объемными долями.

Действительно, если мольной долей назвать отношение числа киломолей каждого газа (М_i) к числу киломолей смеси газов (М), то, учитывая, что

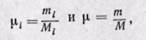
можно написать

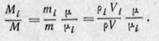
Из закона Авогадро следует, что при одинаковых давлениях и температурах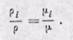

Тогда окончательно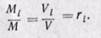

Соотношения между массовыми и объемными долями. Между удельными объемами, плотностями, молекулярными массами и газовыми постоянными какого-нибудь газа и всей смеси в целом на основании закона Авогадро и уравнения Клапейрона — Менделеева существует следующая зависимость:

(3-2)

где р_i — плотность каждого газа; ρ — плотность смеси газов; μi — молекулярная масса каждого газа; μ — молекулярная масса смеси газов.

Можно записать также, что

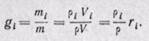
Последние два соотношения позволяют составить несколько уравнений, связывающих массовые и объемные доли:

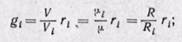(3-2')

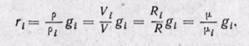(3-2")