Межмодовая дисперсия.

Межмодовая дисперсия возникает вследствие различной скорости распространения у мод, и имеет место только в многомодовом волокне. Для ступенчатого и градиентного многомодового волокна с параболическим профилем показателя преломления ее можно вычислить соответственно по формулам:

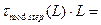
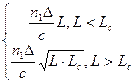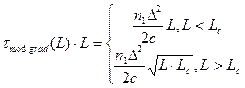; (1.3)

где 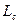- длина межмодовой связи (для ступенчатого волокна порядка 5км, для градиентного – порядка 10км).

Изменение закона дисперсии с линейного на квадратичный связано с неоднородностями, которые есть в реальном волокне. Эти неоднородности приводят к взаимодействию между модами, и перераспределению энергии внутри них. При 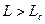наступает установившийся режим, когда все моды в определенной установившейся пропорции присутствуют в излучении. Обычно длины линий связи между активными устройствами при использовании многомодового волокна не превосходят 2км и значительно меньше длины межмодовой связи. Поэтому можно пользоваться линейным законом дисперсии.

Вследствие квадратичной зависимости от D значения межмодовой дисперсии у градиентного волокна значительно меньше, чем у ступенчатого, что делает более предпочтительным использование градиентного многомодового волокна в линиях связи.

На практике, особенно при описании многомодового волокна, чаще пользуются термином полоса пропускания. При расчете полосы пропускания W можно воспользоваться формулой:

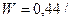τ (1.4)

Измеряется полоса пропускания в МГц/км. Из определения полосы пропускания видно, что дисперсия накладывает ограничения на дальность передачи и верхнюю частоту передаваемых сигналов. Физический смысл W – это максимальная частота (скорость передачи) передаваемого сигнала при длине линии 1км. Если дисперсия линейно растет с ростом расстояния, то полоса пропускания зависит от расстояния обратно пропорционально.