Нелинейные структуры

В качестве примеров нелинейных структур рассмотрим списки, деревья и сети.

Порядок следования (и, соответственно, выборки) элементов таких структур может не соответствовать порядку расположения элементов в памяти. Списки представляют собой пример линейного упорядочения, деревья — двумерного, сети — произвольного. Соответственно различаются методы и средства, обеспечивающие последовательность выборки элементов данных. Обычно для обеспечения возможности прямого доступа к произвольному элементу необходимо использовать вспомогательные структуры типа инвертированных списков.

Списки. Как и массив, список представляет собой совокупность

однотипных элементов. Однако порядок выборки элементов может отличаться от порядка следования в памяти, определенного при размещении. Наиболее очевидный способ установления однонаправленного порядка выборки элементов — это сопоставить каждому элементу списка ссылку, указывающую на следующий элемент. Соответственно, для организации двунаправленного списка, допускающего также выборку в обратном порядке, каждый элемент должен иметь ссылку на предыдущий. Такая организация уже не допускает возможности прямого доступа, например, по номеру элемента.

Кроме того, число элементов списка, как и в случае последовательностей, может быть неизвестно до размещения, и до начала обработки (и, соответственно, размещения) необходимо считать длину списка бесконечной, что ведет к необходимости предусматривать специальную процедуру выделения/освобождения памяти.

Таким образом, с точки зрения физической реализации элемент списка должен быть составным, включающим собственно информативные данные, несущие смысловое значение, и дополнительные данные (ссылки), определяющие порядок доступа к информативным элементам.

Понятие списка достаточно универсально. В общем случае ссылки могут указывать ответвления к другим спискам — подспискам. В зависимости от способа построения списка и предполагаемых путей доступа к элементам различают следующие виды ссылок: перекрестные, боковые, иерархические, множественные, что позволяет изменять «естественный» последовательный порядок прохода по элементам списка.

Деревья. Дерево (рис. 3.7) представляет собой иерархию элементов, называемых узлами. На самом верхнем уровне иерархии имеется только один узел — корень. Каждый узел, кроме корня, связан с одним узлом на более высоком уровне, называемым исходным узлом для данного узла. Каждый элемент имеет только один исходный. Каждый элемент может быть связан с одним или несколькими элементами на более низком уровне, которые называются порожденными.Элементы, расположенные в конце ветви, т. е. не имеющие порожденных, называются листьями.

Существует несколько способов представления структуры дерева. Например, дерево может быть определено как иерархия узлов с попарными связями, в которой:

1. Самый верхний уровень иерархии имеет один узел, называемый корнем.

2. Все узлы, кроме корня, связываются с одним и только одним узлом на более высоком уровне по отношению к ним самим.

Такое определение в части организации связей совпадает со списком, и, в частности, список представляет вырожденный случай дерева, в котором каждая вершина имеет не более одного поддерева.

Еще раз отметим, что деревья здесь рассматриваются как средство и для логического, и для физического представления данных. В логическом описании данных они используются для определения связей между элементами структуры, а при определении физической организации данных — для определения набора указателей, реализующих связи между ними.

Использование ссылок для организации доступа к отдельным элементам структуры не позволяет сократить процедуру поиска, в основу которой положен последовательный перебор. Процедура поиска будет эффективнее, если будет предварительно установлен некоторый порядок перехода кследующему элементу дерева. Такой порядок в ряде случаев определяется в отношении метода обхода и регулярности итераций, определяемой длиной пути и кратностью деления вершины.

Выделяют [2] три метода обхода: сверху вниз, слева направо, снизу вверх.

Регулярность обхода дерева может быть связана с упорядоченными деревьями, к которым относятся сбалансированные и двоичные деревья.

Сбалансированное дерево в каждом узле имеет одинаковое число ветвей, причем процесс включения новых ветвей в узлы дерева идет сверху вниз, а на каждом уровне дерева — слева направо. Для дерева

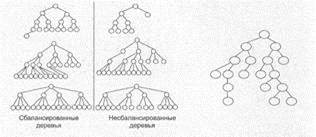
с фиксированным числом ветвей физическая организация данных будет более простой. Однако большая часть логических организаций данных не может быть задана в виде сбалансированной древовидной структуры, и для их представления требуется переменное число ветвей в каждом узле. В то же время индексы могут быть построены в виде сбалансированных древовидных структур.

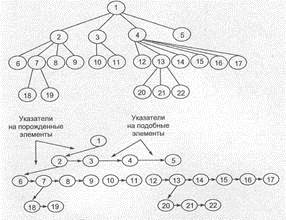
Двоичные деревья — это особая категория сбалансированных древовидных структур, в которой допускается не более двух ветвей для одного узла. Любые связи в дереве можно представить в виде двоичных древовидных структур.

При таком представлении каждый элемент может иметь указатели как на порожденные, так и на подобные элементы.

Различные виды двоичных деревьев, для которых характерно наличие жесткой схемы управления их ростом, достаточно эффективно используются для построения больших поисковых индексов, размещаемых обычно на устройствах внешней памяти. Кроме того, для таких деревьев можно организовать специальное «страничное» хранение поддеревьев, что сократит число физических обращений к устройству.

Заметим, что деревья поисковых индексов являются однородными структурами: каждый узел представлен элементами одного типа. Однако большинство баз должно поддерживать организацию данных, имеющих различную природу. В этом случае при работе с неоднородными

структурами разной глубины, гарантировать регулярность, обеспечивающую эффективность процедур доступа, становится затруднительно.