КРУЧЕНИЕ
Рекомендуемая литература
Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл.5 (§ 5.1–5.4), гл. 11 (§ 11.5);
Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 6 (§ 27, 29–30, 32);
Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 6 (§ 6.1–6.4, 6.6, 6.7).
Основные понятия и формулы
При кручении поперечные сечения стержня поворачиваются вокруг его продольной оси, а продольные волокна при этом искривляются, превращаясь в пространственные кривые. Кручение вызывается парами сил, действующими в плоскости поперечных сечений. В поперечных сечениях стержня возникает одно внутреннее усилие - крутящий момент Мк.
 Рис. 3.1. Правило знаков для крутящего
момента
Рис. 3.1. Правило знаков для крутящего
момента
|
Крутящие моменты в сечениях определяются, как и другие виды усилий, методом сечений. Крутящий момент в сечении равен сумме моментов внешних сил, действующих по одну сторону от сечения, относительно продольной оси стержня. Примем правило знаков для крутящего момента: его положительное направление соответствует повороту сечения по ходу часовой стрелки, если смотреть на сечение со стороны внешней нормали (рис. 3.1).
Напряженное состояние в любой точке поперечного сечения при кручении является чистым сдвигом, и в точках поперечного сечения возникают касательные напряжения.
Касательные напряжения при кручении стержня круглого сечения с радиусом R (или кольцевого сечения с внешним радиусом R) определяются по формуле
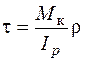 , (3.1)
, (3.1)
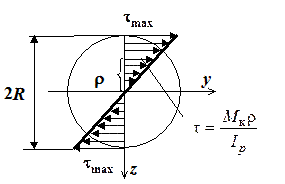 Рис. 3.2. Касательные напряжения
в круглом сечении
Рис. 3.2. Касательные напряжения
в круглом сечении
|
где 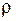 - расстояние от центра до точки, в которой мы определяем t. Эти напряжения направлены перпендикулярно радиусу, соединяющему центр круга с рассматриваемой точкой. Эпюра распределения касательных напряжений на любом диаметре будет иметь вид, показанный на рис. 3.2. Максимальные касательные напряжения, как следует из формулы (3.1), действуют в точках на контуре сечения, они равны
- расстояние от центра до точки, в которой мы определяем t. Эти напряжения направлены перпендикулярно радиусу, соединяющему центр круга с рассматриваемой точкой. Эпюра распределения касательных напряжений на любом диаметре будет иметь вид, показанный на рис. 3.2. Максимальные касательные напряжения, как следует из формулы (3.1), действуют в точках на контуре сечения, они равны
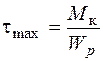 , (3.2)
, (3.2)
где 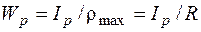 – полярный момент сопротивления.
– полярный момент сопротивления.
Деформацию стержня круглого (кольцевого) сечения при кручении характеризует угол закручивания поперечного сечения на участке длиной 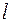 (рис. 3.3)
(рис. 3.3)
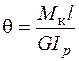 . (3.3)
. (3.3)
 Рис. 3.3. Деформация стержня при кручении
Рис. 3.3. Деформация стержня при кручении
|
Относительная величина этого угла (на единицу длины) 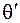 называется погонным углом закручивания
называется погонным углом закручивания
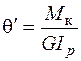 . (3.4)
. (3.4)
Эпюры распределения касательных напряжений в стержнях прямоугольного сечения показаны на рис. 3.4. Максимальные касательные напряжения действуют в точках, расположенных по середине длинной стороны сечения. Они равны
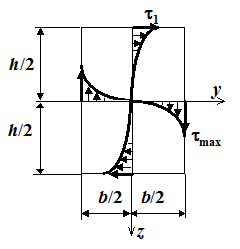 Рис. 3.4. Распределение
касательных напряжений
в прямоугольном сечении
Рис. 3.4. Распределение
касательных напряжений
в прямоугольном сечении
|
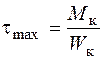 . (3.5)
. (3.5)
Напряжения в точках по середине короткой стороны
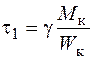 . (3.6)
. (3.6)
Погонный и полный углы закручивания для стержней прямоугольного сечения определяются по формулам
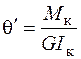 ;
; 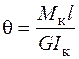 . (3.7)
. (3.7)
Геометрические характеристики сечения, входящие в формулы (3.1)–(3.7), можно найти следующим образом.
Полярный момент инерции и полярный момент сопротивления:
* для круглого сечения
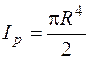 ,
, 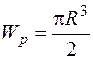 ; (3.8)
; (3.8)
* для кольцевого сечения
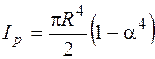 ;
; 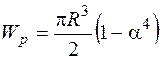 . (3.9)
. (3.9)
Здесь 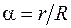 - отношение радиусов внутреннего и внешнего контуров кольца.
- отношение радиусов внутреннего и внешнего контуров кольца.
Для стержня прямоугольного сечения геометрическая характеристика жесткости
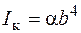 (3.10)
(3.10)
и момент сопротивления кручению
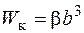 , (3.11)
, (3.11)
где 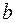 - меньшая сторона прямоугольного сечения, а коэффициенты
- меньшая сторона прямоугольного сечения, а коэффициенты 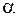 ,
, 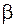 ,
, 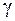 в формулах (3.6), (3.10), (3.11) определяются в зависимости от отношения сторон сечения
в формулах (3.6), (3.10), (3.11) определяются в зависимости от отношения сторон сечения 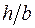 по таблицам, имеющимся в справочной литературе, например в [3, § 6.6].
по таблицам, имеющимся в справочной литературе, например в [3, § 6.6].
Модуль сдвига в формулах (3.3) и (3.7)
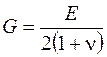 . (3.12)
. (3.12)
Целью расчета вала на кручение, как правило, является удовлетворение двум условиям: прочности и жесткости. Условие прочности в опасной точке вала при кручении записывается так:
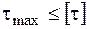 , (3.13)
, (3.13)
где [t] берется либо на основании опытных данных, либо (при отсутствии нужных опытных характеристик) по теориям прочности, соответствующим материалу. Например, из теорий прочности для хрупких материалов, примененных для чистого сдвига, следуют такие результаты:
* из второй теории прочности
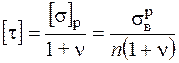 ; (3.14)
; (3.14)
* из теории Мора
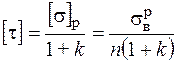 , (3.15)
, (3.15)
где 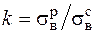 .
.
Из теорий прочности для пластичных материалов при чистом сдвиге получим:
* по третьей теории прочности
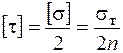 , (3.16)
, (3.16)
* по четвертой теории прочности
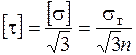 . (3.17)
. (3.17)
Условие жесткости вала при кручении – это условие, ограничивающее деформации стержня, а именно:
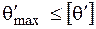 , (3.18)
, (3.18)
где 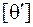 – допускаемый погонный угол закручивания, величина которого нормируется.
– допускаемый погонный угол закручивания, величина которого нормируется.
Удовлетворяя этим двум условиям, можно либо подбирать размеры сечения, либо определять допускаемую нагрузку на стержень.
Дата добавления: 2015-03-07; просмотров: 1460;
