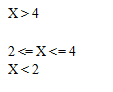Задания для самостоятельной работы. 1. Даны действительные числа c, d

1. Даны действительные числа c, d. Вычислить.

Где x₁ - больший, а x₂ -меньший корни уравнения x² – 3x - /сd/=0

2. Вычислить функцию

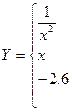
3. Вычислить функцию

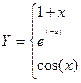
4. Вычислить функцию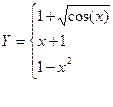

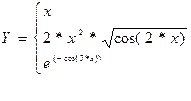
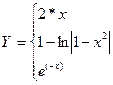
7. Вычислить функцию

8. Вычислить функцию

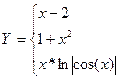
9. Вычислить функцию

10. Вычислить функцию

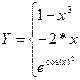
11. Вычислить функцию

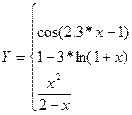
12. Вычислить функцию

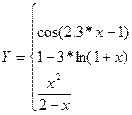
14. Вычислить функцию

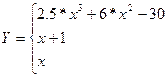
15. Вычислить

sinX, X<0

y=

tgX, X>=0

16. Составить программу вычисления величины M по формулам:

17. Составить программу вычисления функции при заданном x.

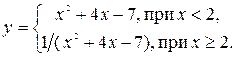
18. Составить программу вычисления функции

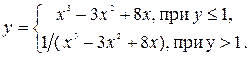
19. Составить программу вычисления функции f(x) вида

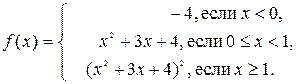
20. Составить программу вычисления значений функции F(x,y) вида

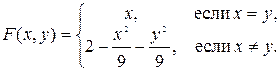
21. Выбрать из чисел 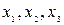наибольшее.

22. Расположить числа 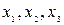в порядке убывания.

23. Составить программу для решения биквадратного уравнения 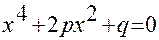при любых действительных p и q.

24. Если среди трех чисел a,b,c имеется хотя бы одно четное вычислить

максимальное, иначе - минимальное

25. Ввести два числа, меньшее заменить полусуммой, а большее – удвоенным

произведением.

26. Ввести три числа A,B,C .Удвоить каждое из них, если A>=B>=C, иначе

поменять значения A и B.

27. Определить является ли точка с координатами X,Y точкой пересечения

диагоналей квадрата со стороной R,одна вершина которого расположена в

начале координат.

28. Определить лежит ли точка с координатами (X,Y) вне круга радиуса R с

центром в точке (A,B) или внутри него.

29.Определить являются ли две точки (X1,Y1, Х2,У2) корнями системы уравнений

ax + by=c

nx + my=d

30. Составьте программу, определяющую, лежит ли точка с указанными координатами X, Y на окружности радиуса R с центром в начале координат.

31. Составьте программу, определяющую, пройдет ли график функции

у=5х² - 7х+2 че­рез заданную точку с координатами (а,Ь).

32. К финалу конкурса лучшего по профессии "Специалист электронного офиса" были допущены трое: Иванов, Петров, Сидоров. Соревнования проходили в три тура. Иванов в первом туре набрал ml баллов, во втором - n1, в третьем - р1. Петров - соответственно m2, n2, р2; Сидоров - mЗ, n3, рЗ. Составьте программу, определяющую, сколько баллов на­брал победитель.

33. Составьте программу, которая по трем введенным вами числам определит

могут ли эти быть длинами сторон треугольника, и если да, то какой получится треугольник с данными длинами сторон (прямоугольный, остроугольный, тупоугольный).

а) на одной диагонали; ^{4 5}

б) на одной вертикали; ^ g

в) на одной горизонтали. •—— —

35. Напишите программу-фильтр, которая при нажатии любых клавиш выводит на экран только буквы и цифры, при этом указывая, что выводится: буква или цифра.

36. Напишите программу, которая по паролю будет определять степень доступности сотрудника к секретной информации в базе данных. Доступ к базе имеют только шесть человек, разбитых на три группы по степени доступа. Они имеют следующие пароли:

9583,1747 — доступны модули базы А, Б, С

3331, 7922 — доступны модули базы Б, С

9455, 8997 — доступен модуль базы С

37. Составьте программу, реализующую эпизод применения компьютера в книжном магазине. Компьютер запрашивает стоимость книг, сумму денег, внесенную покупателем; если сдачи не требуется, печатает на экране "спасибо"; если денег внесено больше, то печатает "возьмите сдачу" и указывает сумму сдачи; если денег недостаточно, то печатает об этом сообщение и указывает размер недостающей суммы.

38. В ЭВМ поступают результаты соревнований по плаванию для трех спорте Составьте программу, которая выбирает лучший результат и выводит его на экран с с нием, что это результат победителя заплыва.

39. Составьте программу, которая по введенному вами k — числу грибов печатает фразу "Мы нашли в лесу k грибов", причем согласовывает окончание слова "гриб" с k. (Количество грибов может быть любым целым числом: 1, 3,

4, 127 и т. п. Окончание фразы определяется значением последней цифры.)

40. Составьте программу, которая для целого числа k (от 1 до 99), введенного

вами напечатает фразу "Мне k лет", где k — введенное число, при этом в нужных случаях слово "лет" заменяя на слово "год" или "года". (Например: при k=70 "Мне 70 лет", при k=l5 "Мне 15 лет", при k=23 "Мне 23 года" и т.п.)

41. Составьте программу для вычисления числа дней в месяце, если даны: номер месяца N — целое число от 1 до 12, целое число А, равное 1 для високосного года и 0 в ном случае.

42. С клавиатуры вводятся длины отрезков а,b,с и d. Оценить их на возможность построения треугольников.

43. Заданы два целых числа. Определить, являются ли они оба четными или оба нечетными или какое из них чет­ное, а какое нечетное.

44. Заданы координаты вершин треугольника и точки. Определить, лежит ли точка внутри треугольника.

45. Написать программу нахождения суммы большего и меньшего из трех чисел.

46. Написать программу, по длинам сторон распознаю­щую среди всех треугольников АВС прямоугольные. Если таковых нет, то вычислить величину угла С.

47. Найти max {min (a, b), min (с, d)].

48. Даны три числа: а, b, с. Определить, какое из них рав­но d. Если ни одно не равно d, то найти max (d - а, d - b, d - с).

49. Даны четыре точки: A1(x1,y1), А2(x2,y2), A3(x3,y3), А4(х4, у4). Определить, являются ли они вершинами парал­лелограмма.

50. Даны три точки: А(х, у,), В(х,,y) и С(x,y,). Опре­делить, расположены ли они на одной прямой. Если нет, то вычислить угол В.

51. Даны вещественные числа а, b, с. Удвоить эти числа, если а< b < с, и заменить их абсолютными значениями, если это не так.

52. На оси ОХ расположены три точки: а, b, с. Опреде­лить, какая из точек, b или с, расположена ближе к а.

53. Даны три положительных числа: а, b, с. Проверить, являются ли они сторонами треугольника. Если да, то вы­числить площадь этого треугольника.

54. Вычислить Х_k-ый член последовательности {Х_n}, где X₀=1,

Xn=n*X_n-1+1/n при n=1,2,3… .

55. С точностью 10^–5 степени вычислить Х - корень уравнения tg(х)=х,

используя метод деления отрезка пополам.

56. Подсчитать k-количество цифр в десятичной записи целого числа n.

57. Дана непустая последовательность натуральных чисел. Определить порядковый номер наименьшего из них.

58. Даны n>0 и последовательность из вещественных чисел среди которых есть хотя бы одно отрицательное число. Найти величину наибольшего среди отрицательных чисел этой последовательности.

59. Даны натуральное число t и вещественные числа a₀, a₁, …,a_n. Вычислить значение многочлена a₀xⁿ+a₁x^n-1+…a _n-1x+a_n и его производной в точке t²+0.5.

60. Вычислить:

1) y=(2n-1)!=1*3*5*…*(2n-1), n>0;

2) y=(2n)!=2*4*…*(2n-1), n>0;

3) y=n! n>0.

61. Вычислить y=Ö3+Ö6+…+Ö96+Ö99

62. Вычислить y=1!+2!+3!+…+n!,где n>0;

63. Числа Фибоначчи (f_n) определяются по формулам

f₀=f₁=1; f_n=f_n-1+f_n-2 при n=2,3,…:

1) определить f – 40-е число Фибоначчи

2) найти f-первое число Фибоначчи, большее m(m>1);

64. Не используя стандартные функции (за исключением аbs), вычислить с

точностью eps>0: y=e^x=1+x/1!+x²/2!+…+xⁿ/n!+… .

Cчитать, что требуемая точность достигнута, если очередное слагаемое по

модулю меньше eps. Все последующие слагаемые можно не учитывать.

65.Вычислить: y=sin1+sin1.1+ sin1.2+…+sin2.

66. Вывести таблицу значений функций sin x и cos x на отрезке [0,1] с шагом 0.1 в следующем виде (считать, что при печати на каждое вещественное число отводится по 6 позиций строки):

67.Вычислить s-сумму квадратов всех целых чисел, попадающих в интервал (ln x, e^x),x>1.

68.Вычислить k-количество точек с целочисленными координатами, попадающих в круг радиусом R(R>0) c центром в начале координат.

69.Дано 15 вещественных чисел. Определить, образуют ли они возрастающую последовательность.

70.Дана последовательность из 10 целых чисел. Определить, со скольких отрицательных чисел она начинается.

71.Определить k-количество трехзначных натуральных чисел,сумма цифр которых равна n (1<=n<=27). Операции деления (l, div и mod) не использовать.

72. При табулировании функции y=ln(x-a) на отрезке [1,10] с шагом h определить второе значение y, больше p.

73.Вычислить сумму ряда, общий член которого задан формулой An=(xⁿ)/n!.

74.В последовательности символов вывести на печать True, если количество

гласных букв больше, чем согласных и FALSE-иначе.

75. В последовательности целых положительных чисел определить

максимальное четное число и его порядковый номер.

76. В последовательности вещественных чисел определить наименьшее

отрицательное число и его порядковый номер.

77. В последовательности целых чисел определить третье положительное число

и подсчитать количество цифр в нем.

78. В последовательности символов выдать на печать TRUE , если значение последнего символа равно Ф.

79. В последовательности чисел выдать на печать TRUE , если значение максимального числа больше числа 10.

80. В последовательности вещественных чисел подсчитать произведение чисел,

кратных 3.

81.В последовательности чисел сравнить, что больше сумма положительных

или произведение отрицательных.

82.В последовательности символов подсчитать количество букв и количество

цифр.

83. В последовательности чисел определить предпоследнее отрицательное число.

83. Составить программу для вычисления суммы

.

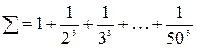84. Составить программу для нахождения суммы

.

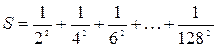85. Составить программу для вычисления величины

,

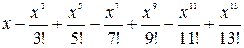86. Составить программу вычисления при заданном x функции y вида

.

87. Последовательность многочленов Н₀(x), Н₁(x), … определяется следующим образом:Н₀(x)=1, Н₁(x)=x, Н_k(x)=xН_к-1(x)-(к-1) Н_к-2(x) (к=2, 3, …).

1) получить Н₃(x), Н₅(x), Н₈(x).

2) даны действительные числа а₀, …, а₈. Получить многочлен

а₀Н₀(х)+…+а₆Н₆.

3) Дано действительное число а.Вычислить Н₀(а)+……+Н₆(а).

88.Даны действительные числа а₀, …, а_n, b₀, …, b_n(a₀,…,a_n попарно различны).Требуется найти многочлен F(x) степени не выше, чем n , такой , что F(a_i)=b_i (i=0,1, …, n).

89. Составить программу для вычисления значения многочлена Чебышева 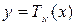при заданном x, используя рекуррентную формулу

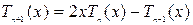, причём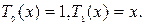

90. Составить программу вычисления величины А, определяемой формулой

.

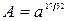91. Составить программы вычисления значений функции y вида

а)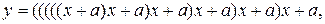

б)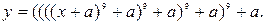

92. Составить программу вычисления суммы вида

.

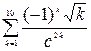92. Cоставить программу для вычисления значения суммы

s= 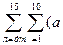^k+1+x^n-1);

93. Составить программу для вычисления выражения

s= 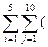x/2)^i/j

для x, изменяющегося от х₀ до х_n с шагом h_n<>1.

94. Cоставить программу для вычисления значения произведения:

p= k²+x/(n+2));

95. Cоставить программу для вычисления значения произведений:

p= 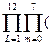L+1)/(10+a^m+L)

для a, изменяющегося от a₀ до a_n c шагом h_a=1.

96. Вычислить значения функции y

y= 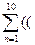x-5)/(n+1))ⁿ⁺¹

для x, изменяющегося от x₀ до x_n с шагом h_x<>1;

97. Вычислить значения функции y=(a*x)! для x, изменяющегося от x₀ до x_n с шагом h_x=1, b, а - с шагом h_a=1;

98. Вычислить значения функции

y=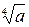+3+ 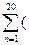a+4)/(2+1/n)ⁿ

для a, от a₀ до a_n с шагом h_a=1.

Составить программу для вывода значений функции z=f(x,y) двух

аргументов x, y действительного типа при x, изменяющихся от x₀ до x_n c

шагом x_n<>1,и y от y₀ до y_n<>1:

99. z=ln((Öx²+y²-b²)/(Ö½x½+sin½y½+b²))

100. z=x²cos(x+y)³+y²sin(x+y)³

101 z=³Öx+5 +⁵Öy+3

102 z= (e^x+1+e^y-1)/e^x+y;

103 z=sin x+ cos y;

104 z=tg x+ ctg y;

105 z=cos x^*sin y+ cos y^*sin x;

106 z=Öcos² x+ sin² y.

СТРОКИ

Символьная информация может быть представлена как отдельными символами так и массивами символов(строками).

Язык Pascal допускает два способа хранения символьных массивов в памяти ЭВМ: распакованный и упакованный. Распакованные массивы символов хранятся в памяти ЭВМ по одному символу в машинном слове, упакованные по одному символу в байте. При описании упакованного массива символов используют служебное слово packed. Описание упакованного массива символов имеет вид:

Var

MAS: Packed Array[1..20] of Char;

Описание распакованного массива символов имеет вид:

Var

M: Array[1..20] of char;

Для преобразования символьного массива из распакованной формы в упакованную и наоборот, из упакованной в распакованную, в язык Pascal

используются две стандартные функции Pack, UnPack.