Задания для самостоятельной работы. 1. Написать программу, которая вводит значения трех переменных: А, В, С
1. Написать программу, которая вводит значения трех переменных: А, В, С
типа word и выводит их сумму.
2. Написать программу, которая вводит значения четырех переменных А, В, С,
D типа integer и выводит их сумму.
3.Написать программу, которая вводит значения двух переменных: А, В
типа integer.
4. Написать программу ввода значений А, В, С и вывести результат выражения
А * (В / 3,14) + (С * 3) в отдельной строке.
5. Написать программу ввода значений R, Y и вывести результат выражения
R * Y2 + (Y/5).
6. Даны два действительных числа a и b . Получить их сумму, разность и
произведение.
7. Составить программу расчета, какую массу соли и воды надо взять для
приготовления раствора массой m г с массовой долей w %.
8. Составить программу исследования положительного вещественного числа А,
в которой определялись бы значения следующих величин: целая часть, дробная часть, значение арифметического квадратного корня, остаток от
деления на 5, символ по целой части числа.
9. Составьте программу, определяющую, сколько времени в минутах затратит студент на дорогу от дома до стадиона, если известна длина этого расстояния S и средняя скорость движения V км/ч? Значения S и V задаются с клавиатуры.
10. Составьте программу, вычисляющую, сколько процентов от А + В — С приходится: а) на А; б) на В; в) на С?
11. Составить программу вычисления времени t встречи автомобилей,
движущихся равноускоренно навстречу друг другу, если известны их скорости 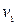 и
и 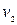 , ускорения
, ускорения 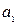 и
и  и начальное расстояние между ними s.
и начальное расстояние между ними s.
12. Даны действительные числа x и y.Получить
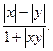
13. Даны два действительных положительных числа. Найти среднее арифметическое и среднее геометрическое этих чисел.
14. Даны  два действительных числа. Найти среднее арифметическое этих чисел и среднее геометрическое их модулей.
два действительных числа. Найти среднее арифметическое этих чисел и среднее геометрическое их модулей.
15. Смешано v1 литров воды температуры t 1 с v 2 литрами воды температуры t2 . Найти объем и температуру образовавшейся смеси.
параллельно.
16. Определить время падения камня на поверхность земли с высоты h.
Даны x, y, z. Вычислить a, b, если.
17. а= 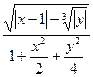
 b=
b= 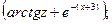
18. а= 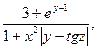 b=
b= 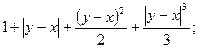
в) а = 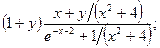 b=
b= 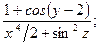
19. а= 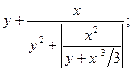

 b=
b= 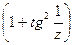

20. Составить программу для вычисления функции y и z по формулам:
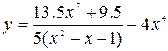
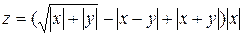
21. Составить программу вычисления величины А по формуле
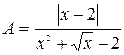
22. Написать фрагмент программы для решения системы из двух уравнений с двумя неизвестными, используя метод определителей:
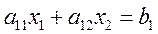 ,
,
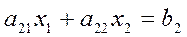 .
.
Метод определителей позволяет найти значения переменных по следующим формулам:
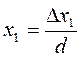 ,
, 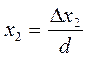 ,
,
23. Вычислить период колебания маятника длины l.
24. Определить силу притяжения F между телами массы m1 и m2 находящимися на расстоянии r друг от друга.
25. Определить время, через которое встретятся два тела, равноускоренно движущиеся навстречу друг другу, если известны их начальные скорости, ускорения и начальное расстояние между ними.
26. Найти сумму членов арифметической прогрессии
a, a+d,…,a+(n-1)d
по данным значениям a, d, n.
27. Вычислить расстояние между двумя точками с координатами
x1 , y1 , и x2 , y2 ,
28.Дано действительное число x. Вычислить 2 x4 – 3 x3+ 4 x2– 5 x+ 6
29. Даны действительные числа x, y. Вычислить
3x2 y2- 2 x y2 -7 x2 y - 4 y2 +15 x y+2 x2 – 3 x + 10 y+ 6
30. Дано действительное число x. Вычислить
а)1 – 2 x + 3 x2 – 4 x3 и b) 1 + 2 x + 3 x2 + 4x3 .
31. Дано число h. Вычислить a и b
а = 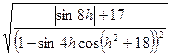 ,
, 
b = 
 1-
1- 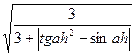
 ,
,
c = 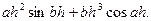
32. Вычислите значение
а) дробной части {x} числаx;
b) остатка от деления натурального числа а на натуральное число b.
33. Составьте программу, которая, используя процедуру Writeln, изображает на экране домик:
*
* *
***********
* *
* *
***********
34. Составьте программу, которая выводит на экран компьютера заставку, аналогичную следующей:
**********************************
* Программа *
* вычисления суммы чисел *
* Автор: Петров В.И. *
**********************************
35. Напишите программу вычисления площади прямоугольного треугольника, значения катетов которого А и В вводятся с клавиатуры. Результат вывести в следующем виде: "Дм значений катетов 4 и 6 площадь прямоугольного треугольника равна 12".
36. Напишите программу вычисления идеального веса человека по формуле: Ид.вес = Рост в см - 100. Значение роста вводите с клавиатуры. Результат вывести в следующее виде: "Для человека ростом 165 см идеальный вес равен 65 кг".
37. Напишите программу получения следующей формы:
*******************************
А * В * А+В * А—В * А/В *
*******************************
6 2 8 4 3.0
*******************************
38. Вы положили деньги в Сбербанк на срочный депозит на три месяца из расчета 60%годовых. Напишите программу, которая вычислит причитающуюся вам через три месяца сумму.
39. Розничная цена мужского костюма составляет Р руб. Торговая скидка в пользу магазина Т% розничной цены. Составьте программу определения оптовой цены костюма.
40. Студент начал решать задачи данного урока программирования, когда электронные часы показывали h1 часов и min1 минут, а закончил, когда было h2 часов и min2 минут. Составьте программу, позволяющую определить, сколько времени студент решал эти задачи. (Будем считать, что задачи решались не дольше суток.)
41. Дано действительное число а. Не пользуясь никакими другими операциями, кроме умножения, получить: а) а4 за две операции; б) а6 за три операции; в) а7 за четыре операции; г) а8 за три операции; д) а9 за четыре операции; е) а10 за
четыре операции; ж) а13 за пять операций; з) а15 за пять операций; и) а21 за шесть операций; к) а28 за шесть операций; л) а64 за шесть операций;
42. Вычислить значение функции х = 3,56(а + b) — 5,8b + 3,8а -1,5 при любых значениях а и b. 21.
43. Даны два целых числа. Найти:
а) их среднее арифметическое;
б) их среднее геометрическое.
44. Известны количество жителей в государстве и площадь его территории. Определить плотность населения в этом государстве.
45. Составить программу решения линейного уравнения ах+Ь=0.
46. Составить программу вычисления значения функции g = 2,8 sin х + \у\ при любых значениях x, y
47. Даны два числа. Найти среднее арифметическое и среднее геометрическое их модулей.
48. Даны два числа. Найти их сумму, разность, произведение, а также частное от деления первого числа на второе.
49. Дано вещественное число х. Не пользуясь никакими другими арифметическими операциями, кроме умножения, сложения и вычитания, вычислить за минимальное число операций 2x4 - Зх3 + 4х2 - 5х + 6.
50. Дано значение х. Получить значение 1 + 2х + Зx2 + 4х3 за минимальное число операций.
51. Найти сумму членов арифметической прогрессии, если известны ее первый член, знаменатель и число членов прогрессии.
52. Составить программу для вычисления пути, пройденного лодкой, если ее скорость в стоячей воде v [км/ч], скорость течения реки v1, [км/ч], время движения по озеру v2 [ч], а против течения v3 [ч].
53. Даны катеты прямоугольного треугольника. Найти его гипотенузу.
100. Даны катеты прямоугольного треугольника. Найти его периметр.
54. Даны основания и высота равнобедренной трапеции. Найти ее периметр.
55. Стороны прямоугольника аи b. Найдите его периметр Р, площадь 5, диагональ d.
56. Стороны параллелограмма а и b, угол между ними х. Найдите периметр Р, площадь S, диагонали d1 и d2.
57. Длины сторон треугольника равны а, b, с. Найдите площадь S, радиус вписанной окружности R, радиус описанной окружности Ro.
58. Длины сторон треугольника a, b, c. Найдите длины На, Нb, Нс его высот.
59. a) Градусная мера угла равна а°. Найдите его радианную меру.
б) Радианная мера угла равна а. Найдите его градусную меру.
60. Найдите длину окружности и площадь круга, радиусы которых R.
61. Радиус окружности равен R. Найдите длины сторон вписанных в эту окружность правильного треугольника, квадрата, правильного шестиугольника.
62. Найдите периметр Р и площадь S правильного п-угольника, вписанного в окружность, радиус которой R..
63. Треугольник задан координатами своих вершин. Найти:
а) периметр треугольника;
б) площадь треугольника;
64. Найти площадь сектора, радиус которого равен 13.7 а дуга содержит заданное число радиан j.
65. Даны действительные положительные числа a, b, c.По трем сторонам с длинами a, b,c можно построить треугольник. Найти углы треугольника.
66. Найти площадь равнобочной трапеции с основаниями a и b и углом a при большем основании a.
67. Треугольник задан длинами сторон. Найти:
а) длины высот;
б) длины медиан;
в) длины биссектрис;
г) радиусы вписанной и описанной окружностей.
68. Дана гипотенуза и катет прямоугольного треугольника. Найти второй катет и радиус вписанной окружности. 
69. Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.
70. Найти площадь кольца, внутренний радиус которого равен 20, а внешний – заданному числу r (r > 20 )
71. Треугольник задан величинами своих углов и радиусом описанной окружности . Найти стороны треугольника.
72. Определить периметр правильного n-угольника, описанного около окружности радиуса r.
73. Даны катеты прямоугольного треугольника. Найти его гипотенузу и площадь.
74. Дана длина ребра куба. Найти объем куба и площадь его боковой
поверхности.
75. Дан правильный треугольник со стороной А, в который вписаны три
одинаковые окружности. Каждая окружность касается двух других и
одной стороны треугольника. Вычислить общую длину окружностей.
76. Задан периметр Р и длины параллельных сторон А, В равнобокой
трапеции. Найти площадь трапеции.
77. Известны длины равных сторон равнобедренного треугольника А и его
высота Н, совпадающая с медианой. Найти площадь описанного вокруг треугольника круга.
78. Даны длины диагоналей параллелограмма А, В и его площадь S.
Определить периметр параллелограмма.
79. Найти площадь выпуклого четырехугольника, в который вписана
окружность, если длины противоположных сторон равны А и С, а периметр четырехугольника равен Р.
80. Даны длины трех сторон треугольника А, В, С. Вычислить в градусах
углы наклона его медиан к соответствующим основаниям.
81. В круг радиусом Р вписана правильная пятиугольная звезда. Найти
площадь этой звезды.
82. В равнобедренном треугольнике известны длины равных медиан М и
угол между ними Х. Вычислить площадь треугольника.
83.Треугольник задан координатами своих вершин (X1, Y1), (X2, Y2) и
(X3, Y3). Найти его периметр и величину наибольшего угла.
84. Найти объем равнобедренной пирамиды с длиной ребра М, основанием
которой является прямоугольник со сторонами К и В.
85.Даны длины трех сторон треугольника А, В, С. Вычислить объем
равнобедренной треугольной пирамиды, построенной на этом треугольнике, если ее высота равна Н.
86.В пирамиду, имеющую в основании прямоугольный треугольник с катетами А и В, вписан шар. Вычислить объем этого шара, если ребро, выходящее из прямого угла основания, имеет длину Н и совпадает с высотой пирамиды.
87.Известны длины параллельных сторон трапеции А, В и расстояние
между ними М. Вычислить объем прямой призмы, содержащей в основании эту трапецию, если высота призмы равна Н.
88.Найти площадь вписанного в ромб круга, касающегося всех его сторон.
Известны длина стороны ромба А и наибольшей диагонали М.
89.Дан равнобедренный треугольник со сторонами А, А, В. Найти длину
вписанной в него окружности.
90.Даны две стороны прямоугольника А и В, на нем построена пирамида,
одно боковое ребро которой перпендикулярно основанию. Длина наибольшего бокового ребра пирамиды равна Е. Найти площадь боковой поверхности.
91.Вычислить площадь кольца, образованного двумя окружностями. Одна
окружность описана вокруг прямоугольного равнобедренного треугольника, а другая - вписана в этот треугольник. Длина катета треугольника равна А.
92.Треугольник задан величинами трех своих углов А, В, С и радиусом
описанной окружности Р. Определить площадь треугольника и сумму длин его высот.
93.Вычислить время Т, через которое упадет тело массой М, брошенное со
скоростью А под углом Н к горизонту.
94.Вычислить общую площадь треугольной призмы высотой Н, имеющей
в основании равносторонний треугольник с длиной стороны А, если призма наклонена к основанию под углом в 60 градусов.
95.Даны длины сторон равнобедренного треугольника А, А, и В. Вычислить расстояние между точкой пересечения медиан и точкой пересечения биссектрис.
96.Центр окружности, вписанной в прямоугольный треугольник, находится на расстоянии Р и Т от вершин острых углов. Найти периметр треугольника.
100.В сектор окружности радиуса Р и углом А вписан круг. Вычислить
площадь круга.
97.Дана длина окружности Р основания конуса и длина образующей Х.
Вычислить объем шара, вписанного в этот конус.
98.Дан диаметр окружности основания Р и длина наклонной образующей
Х. Найти объем вписанного в конус квадрата, одна грань которого
находится в плоскости основания.
99.Составить программу вычисления площади поверхности усечённого
конуса и его объёма.
100.Составить программу вычисления объёма усечённой пирамиды по
формуле:
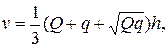
где Q и q- площади оснований , h- высота.
101. Известны длины двух сторон треугольника А,В. Медианы, проведенные к этим сторонам, пересекаются под прямым углом. Найти периметр треугольника.
102. Дана длина ребра куба. Найти объем куба и площадь его боковой поверхности.
103. Определить время падения камня на поверхность земли с высоты h.
104. Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.
105. Треугольник задан координатами своих вершин.
Найти: периметр треугольника, площадь треугольника.
106. Вычислить высоту треугольника, опущенную на сторону а, по известным значениям длин его сторон a, b, c.
107. Вычислить объем цилиндра с радиусом основания r и высотой h.
108. Определить расстояние, пройденное физическим телом за время t, если тело движется с постоянным ускорением а и имеет в начальный момент времени скорость V0
109. Вычислить площадь треугольника по формуле Герона, если заданы его стороны.
110. Определить координаты вершины параболы y=ax2+bx+c. Коэффициенты a,b,c заданы.
111. По данным сторонам прямоугольника вычислить его периметр, площадь и длину диагонали.
112. Даны длины сторон прямоугольного параллелепипеда. Найти его объем и площадь боковой поверхности.
113. Известны координаты двух точек на плоскости. Составить программу вычисления расстояния между ними.
114. Треугольник задан координатами своих вершин. Найти периметр и площадь треугольника.
115. Заданы координаты трех вершин треугольника Найти его периметр и площадь.
116. Найти площадь треугольника, две стороны которого равны а и Ъ, а угол между этими сторонами — у.
117. Дано значение а. Не используя никаких функций и никаких операций, кроме умножения, получить значение а8 за три операции и а10 за четыре операции.
118. Вычислить площадь и периметр правильного N-угольника, описанного около окружности радиуса R (рассмотреть N - целого типа, R - вещественного типа).
119. Определить, во сколько раз площадь круга радиусом R больше площади сегмента, отсеченного хордой длиной А.
120. Найти частное произведений четных и нечетных цифр четырехзначного числа.
121. Найти площадь круга, вписанного в треугольник с заданными сторонами.
122. Окружность вписана в квадрат заданной площади. Найти площадь квадрата, вписанного в эту окружность. Во сколько раз площадь вписанного квадрата меньше площади заданного?
123. Лабораторный анализ установил, что влажность (процентное содержание воды) сахарного песка равна 15 %. Тонну сахарного песка подвергли сушке, и вес его уменьшился на 80 кг. Какова теперь влажность высушенной части товара?


Дата добавления: 2015-01-13; просмотров: 4645;
