Логический синтез вычислительных схем

Рассмотрим логический синтез (создание) вычислительных схем на примере одноразрядного двоичного сумматора, имеющего два входа ("а" и "b") и два выхода ("S" и "Р") и выполняющего операцию сложения в соответствии с заданной таблицей:

где f₁(a,b)=S - значение цифры суммы в данном разряде;

f₂(a,b)=P - цифра переноса в следующий (старший) разряд.

Согласно соотношению (2), можно записать:

S=f₁(a,b)=0*a*b+ 1* ā *b+ 1*a*b +0* ā *b= ā *b+ ą*b;

Р =f₂(a,b) = 1 *a*b + 0* ā *b + 0*a*b + 0* ā* b = a*b.

Логическая схема сумматора, реализующего полученную функцию, представлена на рис. 4.1.

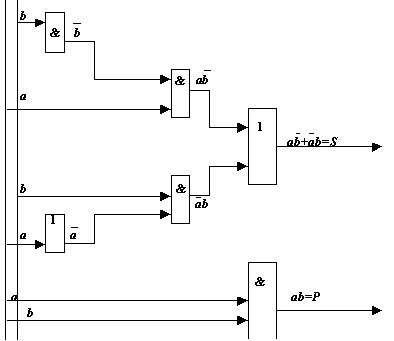
Здесь изображены логические блоки в соответствии с международным стандартом:

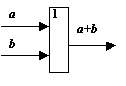схема ИЛИ, реализующая операцию логического сложения

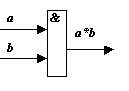схема И, реализующая операцию логического умножения

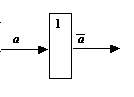схема НЕ, реализующая операцию инверсии

Примечания:1. В ряде случаев перед построением логической схемы устройства по логической функции последнюю, пользуясь соотношениями алгебры логики следует преобразовать к более простому виду (минимизировать).

2. Для логических схем ИЛИ, И и НЕ существуют типовые технические схемы, реализующие их на реле, электронных лампах, дискретных полупроводниковых элементах. Для построения современных ЭВМ обычно применяются системы интегральных элементов, у которых с целью большей унификации в качестве базовой логической схемы используется всего одна из схем: И НЕ (штрих Шеффера), ИЛИ НЕ (стрелка Пирса) или И ИЛИ НЕ.