Иерархические структуры

Дерево (или иерархическая структура) – это конечное множество Т элементов, такое, что выполняются следующие условия:

1. имеется один специально выделенный элемент, называемый корнем дерева;

2. остальные элементы (кроме корня) содержатся в m ≥ 0 попарно не пересекающихся множествах Т₁, ....Т_m, каждое из которых в свою очередь является деревом. Деревья Т₁, ....Т_m являются поддеревьями данного дерева.

Пример дерева показан на рисунке 5:

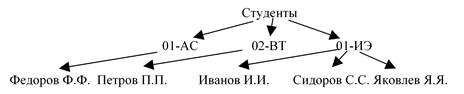
Рисунок 5

Данное дерево представляет состав студентов, например, некоторого факультета, с указанием учебных групп, в которых они числятся. Формально, в соответствии с данным выше определением, в этом дереве можно выделить следующие компоненты:

1. исходное множество Т = {Студенты, 01-АС, 02-ВТ, 01-ИЭ, Федоров Ф.Ф., Петров П.П., Иванов И.И., Сидоров С.С., Яковлев Я.Я.};

2. в качестве корня выступает элемент Студенты;

3. непересекающиеся множества в составе:

· Т₁ = {01-АС, Федоров Ф.Ф.};

· T₂ = {02-ВТ, Петров П.П.};

· Т₃ = {01-ИЭ, Иванов И.И., Сидоров С.С., Яковлев Я.Я.}.

Очевидно, множества Т₁, Т₂, Т₃ также являются деревьями с корнями, соответственно, 01-АС, 02-ВТ, 01-ИЭ. В силу этого можно говорить о том, что данные деревья имеют в составе поддеревья:

· корень – 01-АС, множество Т₁ = {Федоров Ф.Ф.};

· корень – 02-ВТ, множество Т₁ = {Петров П.П.};

· корень 01-ИЭ, непересекающиеся множества Т₁ = {Иванов И.И.}, Т₂ = {Сидоров С.С.}, Т₃ = {Яковлев Я.Я.}.

Аналогичным образом, можно рассматривать вершины, соответствующие фамилиям и инициалам студентов, как вырожденные деревья, представленные только корнями. Для них выполняется условие, когда число непересекающихся подмножеств остальных элементов множества Т равно 0: m = 0.

Таким образом, в дереве рисунка 5 можно выделить несколько деревьев (для лучшего понимания они выделены в отдельные рисунки, корни показаны полужирным шрифтом). Поскольку деревья выделялись последовательно, с каждым шагом выделения деревьев свяжем уровень, начиная с нулевого:

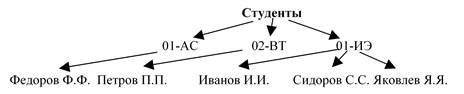
а) исходное дерево – нулевого уровня

б) поддеревья первого уровня

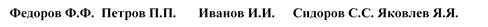
в) поддеревья второго уровня

Рисунок 6

По аналогии с терминологией линейных списков (см. раздел Линейные списки), можно интерпретировать шифры учебных групп (т.е. корни поддеревьев данного дерева) как вторичные ключи, определяющие множества элементов – студентов, числящихся в указанных группах. Фамилии и инициалы студентов можно рассматривать как первичные ключи.

Дадим некоторые определения, которые понадобятся нам в дальнейшем:

1. уровень иерархии – показывает, на каком по счету шаге выделения дерева сформированы данные корни деревьев;

2. подобные элементы – элементы (вершины дерева), расположенные на одном уровне иерархии. Такие элементы, как правило, имеют одинаковую внутреннюю структуру;

3. порожденные элементы– элементы (вершины дерева), расположенные на следующем уровне иерархии;

4. родительские элементы– элементы (вершины дерева), расположенные на предыдущем уровне иерархии.

Введенные понятия прокомментированы на рисунке 7:

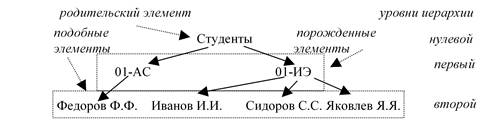
Рисунок 7

Традиционными способами организации хранения иерархических структур являются: множественные ссылки на порожденные элементы, ссылки на подобные и порожденные элементы; кольцевые структуры; справочники; битовые отображения.