Теоретическая часть. Метод крутильного баллистического маятника, используемый в данной работе для определения скорости пули
Метод крутильного баллистического маятника, используемый в данной работе для определения скорости пули, основан на применении закона сохранения момента импульса и основного уравнения динамики вращательного движения твердого тела. Моментом импульса материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением (рис. 11.1):

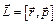 , (11.1)
, (11.1)
где: 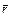 − радиус-вектор, проведенный из точки О в точку А,
− радиус-вектор, проведенный из точки О в точку А, 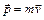 −импульс материальной точки А. Модуль вектора момента импульса:
−импульс материальной точки А. Модуль вектора момента импульса:
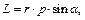 , (11.2)
, (11.2)
где: α – угол между векторами.
При вращении твердого тела вокруг неподвижной оси Z каждая его частица массой mi движется по окружности постоянного радиуса ri с некоторой скоростью υi. Момент импульса отдельной частицы тела равен:
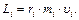 (11.3)
(11.3)
Момент импульса твердого тела относительно заданной оси есть сумма моментов импульса отдельных частиц тела:
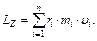 (11.4)
(11.4)
Т.к. 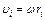 , то следует, что:
, то следует, что:
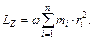 (11.5)
(11.5)
Таким образом, момент импульса твердого тела относительно оси Z равен произведению момента инерции тела относительно той же оси на угловую скорость вращения.
Если продифференцировать по времени это выражение, то получаем уравнение:
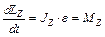 (11.6)
(11.6)
где: ε – угловое ускорение тела, 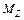 – момент сил, действующих на тело относительно оси Z. Данное уравнение называется основным уравнением динамики вращательного движения и в векторном виде может быть представлено следующим образом:
– момент сил, действующих на тело относительно оси Z. Данное уравнение называется основным уравнением динамики вращательного движения и в векторном виде может быть представлено следующим образом:
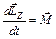 (11.7)
(11.7)
В замкнутой системе момент внешних сил равен нулю и, следовательно, 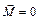 , поэтому:
, поэтому: 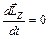 , откуда
, откуда
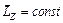 . (11.8)
. (11.8)
Это выражение представляет собой закон сохранения момента импульса: момент импульса замкнутой системы не изменяется со временем.
Примером применения закона сохранения момента импульса и уравнения динамики вращательного движения является удар (соударение) тел, в результате которого одно из них начинает вращаться.
Удар – это столкновение двух и более тел, при котором взаимодействие длится очень короткое время. Абсолютно упругий удар – столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию. Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое. При ударе в телах возникают столь значительные внутренние силы, что внешними силами, действующими на них, можно пренебречь. Это позволяет рассматривать соударяющиеся тела как замкнутую систему и применять к ней законы сохранения.
 Соударение пули с баллистическим крутильным маятником является примером такого взаимодействия. Крутильный маятник представляет собой симметричное тело, подвешенное на тонкой нити (рис.11.2). Если повернуть его в горизонтальной плоскости на угол φ, то в закручивающейся нити подвеса возникают силы, возвращающие тело в начальное положение. При небольших углах закручивания момент этих сил пропорционален величине угла:
Соударение пули с баллистическим крутильным маятником является примером такого взаимодействия. Крутильный маятник представляет собой симметричное тело, подвешенное на тонкой нити (рис.11.2). Если повернуть его в горизонтальной плоскости на угол φ, то в закручивающейся нити подвеса возникают силы, возвращающие тело в начальное положение. При небольших углах закручивания момент этих сил пропорционален величине угла:
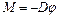 . (11.9)
. (11.9)
где: D – постоянная упругих сил (постоянная кручения).
Когда горизонтально летящая пуля попадает в маятник и застревает в нем – происходит неупругий удар. После удара маятник начинает совершать крутильные колебания относительно тонкой нити. Угол поворота системы определяется уравнением, которое следует из основного закона динамики вращательного движения:
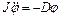 . (11.10)
. (11.10)
где: J – момент инерции колебательной системы.
Решением этого уравнения является:
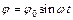 , (11.11)
, (11.11)
где: φ0 – максимальный угол отклонения маятника, ω – частота колебаний маятника. Согласно закону сохранения момента импульса начальные условия для данной системы имеют вид:
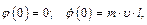 (11.12)
(11.12)
где: m –масса «пули», υ – ее скорость, ℓ – расстояние от оси вращения маятника до точки попадания «пули».
Можно определить, что:
 (11.13)
(11.13)
где: 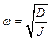 и период колебаний
и период колебаний 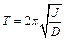 . Из (11.12) и (11.13) следует:
. Из (11.12) и (11.13) следует:
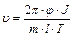 . (11.14)
. (11.14)
Момент инерции для данной колебательной системы можно рассчитать следующим образом:
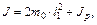 (11.15)
(11.15)
где: m0 – масса груза, ℓ1 = 0,0525 м – расстояние от оси вращения до центров масс грузов, 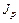 – момент инерции рамки.
– момент инерции рамки.
Период колебаний свободной рамки:
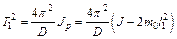 (11.16)
(11.16)
Отсюда следует, что:
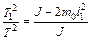 . (11.17)
. (11.17)
Из этого соотношения можно определить момент инерции колебательной системы:
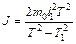 . (11.18)
. (11.18)
Скорость «пули» можно определить из (11.14), используя (11.18):
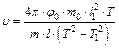 . (11.19)
. (11.19)
Дата добавления: 2015-03-03; просмотров: 740;
