РАЗРАБОТКА НЕФТЯНЫХ И ГАЗОВЫХ

Рис. 12. Последовательное соединение зон.

Рассмотрим передаточную функцию системы, составленной из последовательно соединенных зон. Пусть система включает несколько зон, последовательно соединенных между собой. Тогда в соответствии с определением передаточной функции W_c можно записать

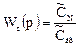
где 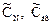— соответственно выходная и входная концентрации, преобразованные по Лапласу.

Умножив и разделив правую часть последнего равенства на 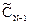, получаем

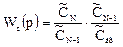
Аналогично, умножив и разделив правую часть уравнения на 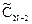, , 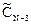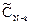приходим к следующему уравнению:

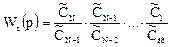
Сомножители 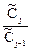(j =1,2 … N) представляют собой не что иное,

как передаточные функции отдельных зон. Тогда уравнение можно записать в виде

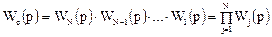
Итак, согласно полученному соотношению, передаточная функция системы W_c(p) из последовательно соединенных зон равна произведению передаточных функций W_j(p) отдельных зон.

Определим среднее время пребывания 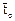в системе, составленной из последовательно соединенных зон. Для этого воспользуемся передаточной функцией системы W_c(p). Пусть N = 2. Тогда

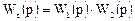
и первый начальный момент системы есть

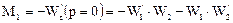
Так как при р= 0 W_l = М₁ = 1 и W₁^’ = Μ₁; W₂^' = -М₂ (здесь М₁ и М₂ - первые начальные моменты первой и второй зон соответственно), то

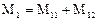
Рассматривая аналогично случаи Ν— 3, 4,..., получаем следующую формулу для среднего времени пребывания в системе:

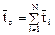
Найдем теперь дисперсию функции отклика системы, составленной из последовательно соединенных зон. Аналогично предыдущему будем использовать передаточную функцию системы. Рассмотрим случай N = 2. Тогда второй начальный момент есть

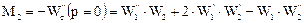
Так как W₁(p=0)=l, a W₂(p = 0) = -Μ₂, то

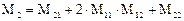
Отсюда находим дисперсию функции отклика системы:

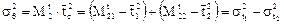
где 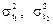— дисперсии функции отклика составляющих зон.

Аналогично рассматривая случаи N = 3, 4, ..., получаем следующее соотношение для дисперсии функции отклика системы из N зон:

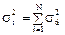
Соответственно безразмерная дисперсия есть

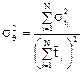
РАЗРАБОТКА НЕФТЯНЫХ И ГАЗОВЫХ