Задание

Упражнение 1. Снять зависимость тока диода 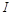от анодного напряжения 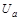. Зависимость 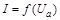представить графически и сравнить с теоретической зависимостью, для чего построить график зависимости квадрата анодного тока от куба напряжения между анодом и катодом диода.

Упражнение 2. Вычислить величину удельного заряда электрона 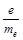на основании уравнения Богуславского–Ленгмюра по формуле (10) и подсчитать ошибку вычисления.

Контрольные вопросы

1. Что называется электровакуумными приборами? Типы электровакуумных приборов.

2. В чем заключается явление термоэлектронной эмиссии? Как определяется работа выхода электрона из металла?

3. Электровакуумный диод: схема, устройство и принцип работы («выпрямление» переменного тока).

4. Роль объемного пространственного заряда в работе диода.

5. Вольт-амперная характеристика вакуумного диода.

6. Режим насыщения анодного тока (когда достигается)?

7. Вывод формулы Богуславского–Ленгмюра.

8. Как можно определить удельный заряд электрона (методика определения).

9. Принцип работы транзистора Т в схеме эксперимента.

10. Объяснить принцип работы экспериментальной схемы.

11. Как измеряется анодный ток ?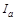

12. Как измеряется анодное напряжение ?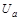

13. Методика расчета ошибки вычисления удельного заряда.

14. На каком участке вольт-амперной характеристики можно использовать формулу Богуславского–Ленгмюра? Почему?

ПРИЛОЖЕНИЕ 1

Закон степени 3/2

Для диода, работающего в режиме объемного заряда, анодный ток и анодное напряжение связаны нелинейной зависимостью, которая выражается законом трех вторых.

Рассмотрим зависимость силы тока, протекающего в вакууме между электродами, от приложенной разности потенциалов. Электроды будем считать плоскими, а ось 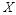направим нормально поверхности электродов. Потенциал катода примем за нуль 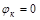, а потенциал анода обозначим 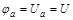(рисунок 1П1).

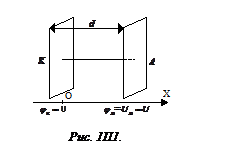
Допустим, что площади пластин катода и анода достаточно велики и при расчете плотности тока вблизи линии, соединяющей центры электродов, можно пренебречь изменением величин в направлениях, перпендикулярных этой линии, считая все величины зависящими только от координаты .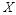

Уравнение Пуассона для потенциала имеет вид:

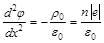, (1П1)

где 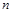– концентрация электронов.

Закон сохранения энергии для электронов, движущихся между анодом и катодом, запишется как:

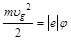, (2П1)

где 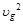– скорость движения электронов в точке с потенциалом .

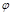Объемная плотность тока в этой точке:

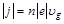. (3П1)

Все величины в правой части (3П1) являются положительными. Вычислив из уравнения (2П1) скорость 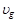, и подставив в уравнение (3П1), находим:

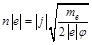. (4П1)

С учетом уравнения (4П1) уравнение Пуассона преобразуется к виду:

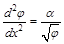, (5П1)

где 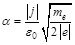– постоянная.

Умножая обе части уравнения (5П1) на 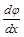, получаем:

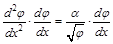. (6П1)

Учитывая, что:

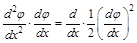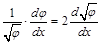; , (7П1)

уравнение (6П1) запишется в виде:

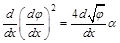. (8П1)

Теперь можно проинтегрировать обе части полученного уравнения (8П1) по 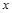в пределах от 0 до того значения 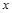, при котором потенциал равен 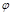. Тогда:

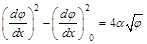, (9П1)

где учтено, что .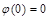

Выше было показано, что напряженность поля на катоде равняется нулю, а, следовательно, и 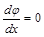. Поэтому получаем:

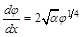(10П1)

или

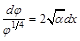. (11П1)

Интегрируя обе части уравнения (11П1) в пределах от 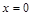, 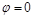до 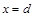, 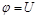получаем:

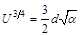. (12П1)

Возводя обе части в квадрат и учитывая, что: 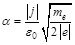, получаем:

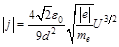(13П1)

или

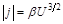, (14П1)

где .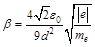

Учитывая, что плотность тока есть:

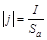, (15П1)

где 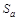– действующая площадь анода, получим зависимость силы тока, протекающего в вакууме между электродами, от приложенной разности потенциалов:

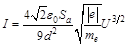. (16П1)

Расчет аналогичной задачи для коаксиальных цилиндрических электродов, для концентрических сферических электродов приводит к такому же виду зависимости объемной плотности тока от разности потенциалов в степени три вторых. В случае коаксиальных сферических электродов выражение, называемое «законом 3/2» или уравнением Богуславского–Ленгмюра имеет вид:

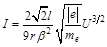. (17П1)

где 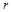– радиус анода, 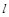– длина катода, 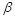– коэффициент, зависящий от отношения радиусов анода и катода.

Теоретическое рассмотрение вопроса о зависимости анодного тока от величины анодного напряжения в вакуумном диоде было проведено при следующих допущениях:

1) начальные скорости электронов, эмитируемых катодом, настолько малы, что можно считать их равными нулю;

2) анодный ток далек от насыщения;

3) объемный заряд создает такое распределение потенциала, что непосредственно у поверхности катода напряженность электрического поля равна нулю.

ЛАБОРАТОРНАЯ РАБОТА № 4

ИЗУЧЕНИЕ РЕЛЕКСАЦИОННЫХ ПРОЦЕССОВ В RC-ЦЕПИ

Цель работы: изучение зависимости тока и напряжения от времени в цепях, содержащих RC-элементы.

Приборы: универсальный лабораторный стенд, осциллограф, омметр, сменная плата, соединительные провода со штекерами.