Мал. 2.1. Мал. 2.2.
Розмірність напруженості електричного поля в системі СІ: [Е] = Н/Кл = В/м. Графічно електричне поле зображують за допомогою ліній напруженості (силових ліній). Силові лінії - лінії, дотичні до яких в кожній точці електричного поля збігаються з вектором напруженості у цій точці. Силові лінії електростатичного поля незамкнені: вони починаються на позитивних зарядах і закінчуються на негативних або продовжуються у нескінченність (мал. 2.1). Густота
силових ліній, тобто їх число на одиницю площі, пропорційна до модуля напруженості.
Скалярну фізичну величину, яка дорівнює dN = E*dS*cosα, називають потоком вектора напруженості електричного поля через поверхню площею dS. Тут 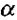 - кут, утворений вектором нормалі до поверхні п і вектором Е (мал. 2.2).
- кут, утворений вектором нормалі до поверхні п і вектором Е (мал. 2.2).
Поряд з напруженістю для характеристики електричного поля використовують ще одну векторну величину -електричну індукцію D. Електрична індукція не залежить від діелектричних властивостей середовища, а отже, не змінюється при переході з одного середовища в інше. Для поля у вакуумі:
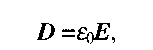 (2.2)
(2.2)
де 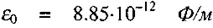 - абсолютна діелектрична
- абсолютна діелектрична
проникність вакууму (електрична стала).
Для ізотропного середовища з відносною діелектричною проникністю ε
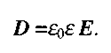 (2.3)
(2.3)
Розмірність електричної індукції в системі СІ: [D] =(Кл2/Н*м2)*Н/Кл = Кл/м2.
Електростатичне поле потенціальне, тобто робота його сил по переміщенню електричного заряду q між двома точками не залежить від форми траєкторії, а визначається лише початковим та кінцевим положеннями заряду. Як відомо, робота сил потенціального поля дорівнює зменшенню потенціальної енергії:
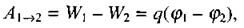 (2.4)
(2.4)
де ф - потенціал. Потенціал - скалярна фізична величина, яка характеризує здатність поля здійснювати роботу і визначається відношенням потенціальної енергії пробного заряду, вміщеного в дану точку поля, до величини цього заряду
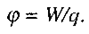 (2.5)
(2.5)
Розмірність потенціалу:  . Безпосередній фізичний зміст має не сам потенціал, оскільки він, як і потенціальна енергія, визначається з точністю до сталого доданка, а різниця потенціалів. Різниця потенціалів U називається напругою:
. Безпосередній фізичний зміст має не сам потенціал, оскільки він, як і потенціальна енергія, визначається з точністю до сталого доданка, а різниця потенціалів. Різниця потенціалів U називається напругою:
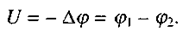 (2.6)
(2.6)
Геометричне місце точок, що мають однаковий потенціал, називають еквіпотенціальною поверхнею (на мал. 2.1 зображені пунктирними лініями). При переміщенні заряду вздовж еквіпотенціальної поверхні 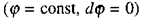 робота над зарядом не виконується. Це означає, що сили електричного поля, а отже, і лінії напруженості перпендикулярні до еквіпотенціальних поверхонь.
робота над зарядом не виконується. Це означає, що сили електричного поля, а отже, і лінії напруженості перпендикулярні до еквіпотенціальних поверхонь.
Зв'язок між напруженістю і потенціалом. Розглянемо переміщення позитивного точкового заряду dl на достатньо малу відстань з точки 1 в точку 2, на якій силу  можна вважати постійною (мал. 2.3). Тоді робота
можна вважати постійною (мал. 2.3). Тоді робота
 (2.7)
(2.7)
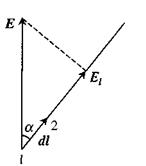
Мал. 2.3
де а - кут між векторами переміщення та сили. Припустимо, що через - точки 1 та 2 проходять еквіпотенціальні поверхні з потенціалами 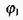 та
та 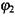 , тому з іншого боку згідно з (2.4)
, тому з іншого боку згідно з (2.4)
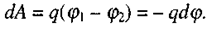 (2.8)
(2.8)
Прирівнявши цей вираз та (2.7), матимемо:
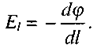 (2.9)
(2.9)
Це рівняння виражає зв'язок напруженості електричного поля з потенціалом: проекція вектора напруженості поля на заданий напрям дорівнює швидкості зменшення потенціалу в цьому напрямі. Можна сказати, що вектор напруженості електричного поля в будь-якій точці дорівнює градієнту потенціали, взятому зі знаком "-".
 (2.10).
(2.10).
Таким чином, вектор напруженості електричного поля збігається з напрямком найбільшої зміни потенціалу. Знак "-" у формулі (2.10) показує, що вектор Е спрямований в бік зменшення потенціалу.
Якщо поле однорідне (Е - const), то остання формула набирає вигляду, відомого з шкільного курсу фізики:
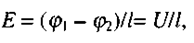 (2.11)
(2.11)
де l - відстань вздовж напрямку Е між точками з потенціалами  та
та 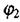
Принцип суперпозиції електричних полів.Розглянемо сукупність точкових електричних зарядів 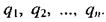 Кожний із цих зарядів створює власне електричне поле Е, незалежно від наявності інших зарядів. Для знаходження результуючого електричного поля в заданій точці застосовується принцип суперпозиції, який полягає в тому, що електричні поля окремих зарядів складаються. Напруженість Е результуючого електричного поля системи точкових зарядів визначається векторною сумою напруженостей полів еі, створених окремими зарядами:
Кожний із цих зарядів створює власне електричне поле Е, незалежно від наявності інших зарядів. Для знаходження результуючого електричного поля в заданій точці застосовується принцип суперпозиції, який полягає в тому, що електричні поля окремих зарядів складаються. Напруженість Е результуючого електричного поля системи точкових зарядів визначається векторною сумою напруженостей полів еі, створених окремими зарядами:
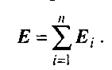 (2.12)
(2.12)
Потенціал результуючого поля (р дорівнює алгебраїчній сумі потенціалів % полів, створених окремими точковими зарядами:
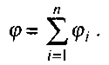 (2.13)
(2.13)
Формули (2.12) та (2.13) використовують для обчислення напруженості та потенціалу електричного поля, створеного будь-якими зарядженими тілами.
Дата добавления: 2015-03-03; просмотров: 899;
