Деформація поздовжнього розтягування чи стиснення

Розглянемо деформацію тіла у випадку, коли один кі­нець його закріплений, а до другого прикладено зовнішню силу F, яка розтягує це тіло.

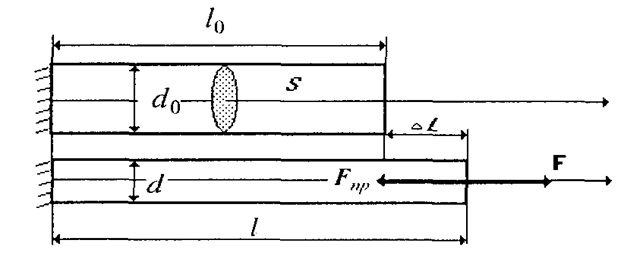
Мал. 1.2. Деформація розтягу бруска.

Відносна деформація у цьому випадку дорівнюватиме

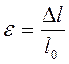
де Δl - зміна довжини зразка під дією зовнішньої сили, l₀ -первісна довжина зразка.

У статичному стані зовнішня сила F урівноважується силами пружності F_пр , що виникають у тілі при деформації (мал. 1.2).

Закон Гука матиме вигляд:

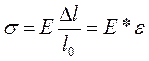(1.3)

де σ=F/S - нормальне напруження, оскільки діюча сила перпендикулярна до площі перерізу зразка S. Модуль пруж­ності Е зветься модулем Юнга. Із закону Гука випливає, що Е =σ , якщо ε=1, тобто якщо Δl = l₀ . Інакше кажучи, мо­дуль Юнга Е дорівнює нормальному напруженню, яке ви­никло б у зразку при збільшенні його довжини вдвічі, якщо б для таких великих деформацій був справедливий закон Гука.

Зауважимо, що при стисненні зразка модуль Юнга від­повідає такому напруженню, при якому довжина зразка прямує до нуля. Розтяг (або стиснення) зразків завжди су­проводжується їх поперечним звуженням (або розширен­ням), тобто зміною їх поперечних розмірів: Δd=d-do. Відношення відносної зміни поперечного розміру до відносної зміни поздовжнього розміру називається коефіці­єнтом Пуассона

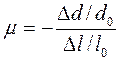, (1.4)

Оскільки Δd < 0 при Δl > 0, то μ > 0. Для матеріалів, що погано стискаються, μ ≈1/2. Майже всі біологічні ма­теріали, в тому числі і стінки кровоносних судин, майже не стискаються, тому для них μ ≈1/2. Далі ми будемо розгля­дати тільки ізотропні середовища, реологічні властивості яких однакові у всіх напрямках.

Деформація всебічного розтягу або стиснення (об'ємна деформація)

Об'ємна деформація виникає при рівномірному роз­поділі стискуючих або розтягуючих сил по поверхні тіла (мал.1.3а).

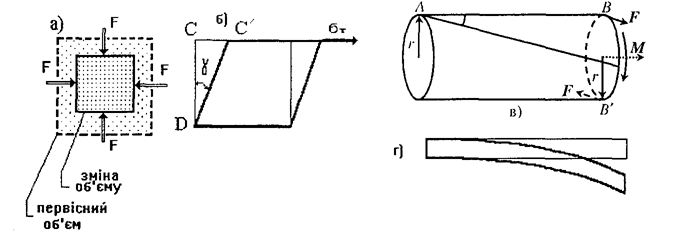
Мал. 1.3. Види деформацій: а) об'ємна деформація, б) деформація зсуву, в) кручення, г) згину.

Закон Гука у цьому випадку матиме вигляд:

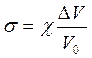
де χ- модуль об'ємної пружності, ΔV та V₀- зміна об'єму тіла та первісний об'єм відповідно. Прикладом напруження, що викликає об'ємну деформацію, є трансмуральний тиск, що дорівнює різниці тисків всередині і зовні судини Р_тр = Р_в - Р₃. Тоді закон Гука набуває вигляду

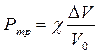(1.5)