Электрические соотношения в идеальном трансформаторе

Назовем идеальным такой трансформатор, в котором:

1) отсутствуют потери энергии (активные сопротивления обмоток равны нулю и потери на вихревые токи в стали магнитопровода также равны нулю);

2) магнитная проницаемость µ_с = ∞ стали магнитопровода, в листах стали магнитопровода нет разъемов и стыков;

3) все линии магнитной индукции проходят целиком по магнитопроводу и каждая линия сцепляется со всеми витками первичной (w₁) и вторичной (w₂) обмоток.

При соблюдении последнего условия электромагнитная связь между первичной и вторичной цепями является полной и коэффициент электромагнитной связи обмоток трансформатора «С» равен единице.

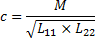(1)

Где L₁₁ и L₂₂ – собственные индуктивности, а M – взаимная индуктивность обмоток

ЭДС первичной и вторичной обмоток такого трансформатора при синусоидальных переменных потоках соответственно равны:

(ЭДС первичной обмотки) e ₁ = - w₁ (d Ф/dt); (1)

(ЭДС вторичной обмотки) e ₂ = - w₂ (d Ф/dt); (2)

где w ₁ и w ₂ , - число витков в первичной и вторичной обмотках трансформатора.

Ф – амплитуда магнитного потока трансформатора.

Действующие значения этих ЭДС:

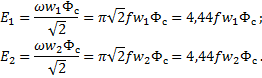(3)

где ω – круговая частота равная 2πf;

f – линейная частота, Гц.

Так как в идеальном трансформаторе падения напряжения отсутствуют, то напряжение и ЭДС равны друг другу:

U₁ = E₁ ; U₂ = E₂ (4)

где U – напряжение;

Е – ЭДС;

I – ток;

W – число витков;

Ф – магнитный поток;

Р – мощность..

На основании выражений (3) и (4) определяется параметр: коэффициент трансформации «К» как:

K = U₁/U₂ = E₁/E₂ = I₂/I₁= W₁/W₂ (5))

Поскольку в идеальном трансформаторе потери активной и реактивной энергии отсутствуют, то:

Р₁=U₁ × I₁ = U₂ × I₂ = Р₂ (6)

Таким образом, в идеальном трансформаторе первичное и вторичное напряжение прямо пропорциональны, а первичный и вторичный токи обратно пропорциональны числам витков соответствующих обмоток. В реальном трансформаторе полученные соотношения несколько нарушаются, однако в трансформаторах с ферромагнитными магнитопроводами эти отклонения при нагрузках, близких к номинальным, относительно малы.