Сітка споживача
| Набір товарів | N1 | N2 | N3 | N4 |
| Котлети, шт. | ||||
| Пиріжки, шт. |
За даними табл. 2.1 можна побудувати відповідний графік (рис. 2.2). Крива на цьому графіку називається кривою байдужості. Крива байдужості для певного споживача – це усі ті комбінації товарів, які забезпечують однаковий рівень задоволення, тобто між наборами товарів N1, N2, N3, N4 споживач не вбачає ніякої різниці.
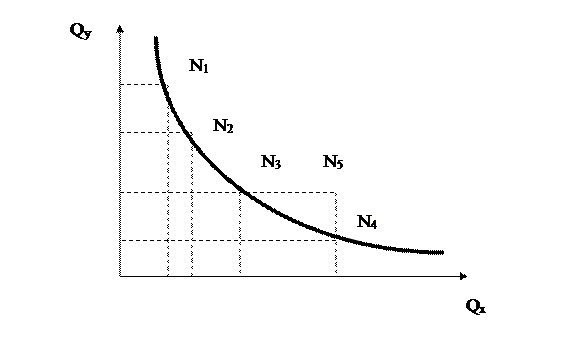

Рис. 2.2. Крива байдужості
Набір товарів, що відповідає координатам точки N5, забезпечує рівень задоволення споживача більший, ніж будь-який набір, що належить кривій байдужості. Однак можна знайти інші набори, що мають таку саму корисність, як і набір у точці N5 . Тому через будь-яку точку, що відповідає певному набору товарів, можна провести криву байдужості. Ці криві утворюють карту кривих байдужості (див. рис. 2.3).
Карта кривих байдужості має певні властивості, а саме:
1. Набори товарів на кривих, більше віддалених від початку координат, відповідають вищому ступеню споживацького задоволення, ніж ті, що лежать на менш віддалених кривих.
2. Криві байдужості не перетинаються. Якщо припустити, що криві байдужості U1 і U2 перетнулися, то вони мають спільну точку А. Тоді набір товарів А має таку саму корисність, що і набір В, що належить кривій U1, та набір С, що міститься на кривій U2 . За принципом транзитивності В = С. Однак це неможливо, оскільки ці точки належать до різних кривих байдужості.


Рис. 2.3. Карта кривих байдужості
Аналізуючи криві байдужості, слід звернути увагу на здатність товарів до взаємозамінювання. Зменшення споживання котлет на певну кількість може бути компенсоване збільшенням споживання пиріжків і навпаки. При цьому споживач буде перебувати на одній і тій самій кривій байдужості, тобто отримуватиме однакове задоволення. Гранична норма заміщення(субституції) – це кількість товару Y, від якого споживач відмовився б, щоб отримати ще одну одиницю товару X, залишаючись на цій кривій байдужості.
Як бачимо з рис. 2.4, зменшення обсягу споживання товару Y на ΔQу (Qу2 - Qу1) компенсується збільшенням споживання товару X на ΔQx (ΔQx2 – Qx1 ). Тому граничну норму заміщення (MRSxy) можна розрахувати таким чином:
MRSxy =– (ΔQу/ ΔQx). (2.3)
Не важко помітити, що при пересуванні вниз по кривій байдужості гранична норма заміщення зменшується. В основі цього процесу лежить дія закону спадної граничної корисності. Гранична корисність (МU) – це приріст задоволення, який отримує людина, споживаючи додаткову одиницю товару. Граничну норму заміщення можна легко виразити співвідношенням граничної корисності товару X та Y, тобто
ΔQx MUx = – ΔQy MUy; (2.4)
MRSxy = – (ΔQу/ ΔQx) = MUx / MUy . (2.5)
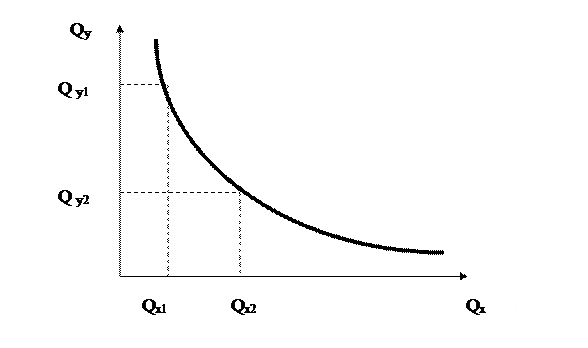
 Рис. 2.4. Гранична норма заміщення
Рис. 2.4. Гранична норма заміщення
Оскільки при збільшенні обсягів споживання якогось товару ступінь задоволення потреб споживача зростає, то від кожної нової порції він матиме менше задоволення, ніж від попередньої. Цю залежність і відображає закон спадної граничної корисності. При пересуванні по кривій байдужості вниз споживання товару X зростає, і його гранична корисність зменшується, а споживання товару Y зменшується, і його гранична корисність зростає, тому дріб у формулі буде зменшуватися.
Дата добавления: 2015-01-13; просмотров: 1541;
