Реферат
Для описание сотовых сухопутных подвижных систем электросвязи (ССПСЭ) используется терминология принятая в рекомендациях МСЭ-R. Для связи базовых станций (БС) и мобильных станций (МС) организуется радиоинтерфейс. Для обозначения системы радиоинтерфейсов введен термин – система подвижной радиосвязи (СПР). Как правило, СПР используют радиоволны диапазона №9 по международной классификации. Фрагмент классификационной табл1.
Табл.1.
| Диапазон радиочастот | Диапазон радиочастот | |||
| Номер | название, обозначение | границы, МГц | границы, дм | название, обозначение |
| очень высокие, ОВЧ | 30…300 | 100…10 | метровые, М | |
| ультравысокие, УВЧ | 300…3000 | 10…1 | дециметровые, ДМ |
Радиоволны эти диапазонов имеет два механизма распространения:
- земная волна распространяется в пределах прямой видимости (радиогоризонта) вдоль поверхности земли;
- тропосферная радиоволна распространяется на сотни км. за счет рассеяния энергии в тропосфере;
Дальность радиогоризонта зависит от высоты подвеса антенн. Как правило, высота антенны БС (h1) составляет десятки – сотни метров, высота антенны МС (h2) – несколько метров. Для инженерных расчетов дальность радиогоризонта может быть определена выражением:
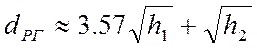 ,
,
где 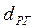 выражено в километрах, h1, h2 – в метрах.
выражено в километрах, h1, h2 – в метрах.
В городских условия здания практически исключают возможность прямой видимости между антеннами БС и МС, и мощность принятого сигнала оказывается значительно ниже, чем в свободном пространстве.
Например, в среднем, дополнительное ослабление в городе на чистоте f = 900 МГц составляет 20…30 дБ при протяженности трассы от 1 до 10 км. Это ослабление вызвано в основном отражением и рассеянием энергии сигнала на крупных строениях. Принимаемый сигнал имеет многолучевую структуру и подвержен глубоким замиранием.
Согласно основному уравнению передачи, уровень мощности принимаемого сигнала:
pс = pо (f, r) + V (t),(1.1)
где pо (f, r) = pП + q1 + q2 – (асв + а1 + а2) –уровень мощности сигнала в точке приема при распространении в свободном пространстве;
pП– уровень мощности передатчика БС;
q1, q2 – коэффициент усиления передающей и приемной антенны соответственно, выраженный в децибелах;
а1, а2– потери в фидере передающей и приемной антенны соответственно;
асв = (4 π r / λ)2 –ослабление свободного пространства;
r – протяженность трассы;
λ – рабочая длина волны;
V (t) – множитель ослабления поля свободного пространства.
Рельеф местности существенно влияет на уровень сигнала. Известны два основных метода для учета его влияния: детерминированный и статистический. Первый позволяет рассчитать ослабление сигнала на трассах с конкретным профилем местности. Применяется для линии связи по схеме «от точки к точке», например, для РРЛ. В этом случае медианное значение мощности сигнала в точке приема – это то, которое превышается в течении 50% времени наблюдения (например, месяца). В СПР, где БС должна обеспечить связь на территории соты часто применяют статистический метод, при котором параметры рельефа (высота препятствий, их форма и взаимное расположение, наклон местности и т.п.) считаются случайными величинами. Рельеф местности в соте оценивают параметрами, усредненными на участках трассы протяженностью 5…10 км.
Выбор энергетических параметров радиоинтерфейса должен обеспечить уверенный прием в зоне обслуживания БС. В точках, расположенных на границах соты, уровень принимаемого сигнала будет различаться из-за неодинакового влияния застройки и рельефа местности. Поэтому в СПР определяет усредненную медианную мощность сигнала (УММС) путем усреднения по двум параметрам; по времени и по местоположению (по числу точек приема). УММС – это такое значение, которое превышается в течение 50% времени месяца и в 50% точек приема, находящихся на данном расстоянии от передающей станции.
1. МОДЕЛИ ДЛЯ ПРЕДСКАЗАНИЯ УРОВНЯ СИГНАЛА
1.1. Модель Окамуры
Существует ряд моделей для прогнозирования уровня радиосигнала в СПР. Модель Окамуры разработанана основании оригинальных экспериментальных исследований автора. Модель Окамуры включает понятие «квазигладкая» местность. Это территория протяженностью в несколько километров, на которой средняя высота неровностей не превышает 20 метров.
В модели Окамуры приняты базовые значения высоты антенны МС h1 = 3м и эффективной высоты антенны БС h2 = 200 м, причем последняя определяется над уровнем квазигладкой поверхности. Для квазигладкой местности уровень УММС
РМ (r) = рO (¦, r) – аМ (¦, r) + H1 (h1, r) + H2 (h2, ¦)(1.2)
где аМ (¦, r) – дополнительное ослабление сигнала в городе (медианное значение), определенное для квазигладкого городского района при базовых высотах антенн БС и МС; H1 (h1, r) – коэффициент «высота - усиление антенны БС», учитывающий, что высота антенны БСможет отличаться от значения 200м; H2 (h2, ¦) – коэффициент «высота-усиление антенны МС», учитывающий влияние реальной высоты антенны МС.
|
|
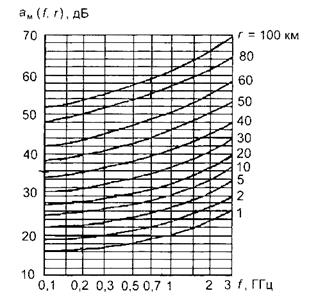
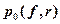 может быть рассчитан по (1.1). Все остальные величины в (1.2) Окамура получил экспериментально, и они представлены в виде графиков, дополнительное ослабление сигнала в городе также определяется графически на рис.1.
может быть рассчитан по (1.1). Все остальные величины в (1.2) Окамура получил экспериментально, и они представлены в виде графиков, дополнительное ослабление сигнала в городе также определяется графически на рис.1.
Экспериментально установлено (рис.2.), что влияние высоты антенны БС зависит от расстояния между МС и БС и практически не зависит от частоты в диапазоне 200…2000 МГц. На рис. 2 номера кривых соответствуют трассам: (1) 70 км 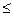 r < 100 км; (2) r = 40 км; (3) r= 20 км; (4) 1 км
r < 100 км; (2) r = 40 км; (3) r= 20 км; (4) 1 км 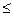 r < 10 км; (5) r=1 км; (6) r=100 км; (7) r=70 км; (8) r=10 км; (9) r=20 км; (10) r=40 км.
r < 10 км; (5) r=1 км; (6) r=100 км; (7) r=70 км; (8) r=10 км; (9) r=20 км; (10) r=40 км.
|
При r 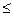 10 км мощность принимаемого сигнала изменяется пропорционально квадрату высоты антенны, а при r
10 км мощность принимаемого сигнала изменяется пропорционально квадрату высоты антенны, а при r  30 км пропорционально кубу
30 км пропорционально кубу  высоты, так что
высоты, так что
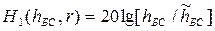 при r
при r 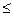 10 км (1.2а)
10 км (1.2а)
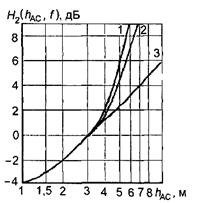
 при r> 30 км (1.2б)
при r> 30 км (1.2б)
При r>dРГуровень сигнала на входе приемника определяет дифракционная составляющая электромагнитного поля. При этом чем выше установлены антенны БС, тем больше уровень принимаемого сигнала. Как правило, высота антенны БС составляет десятки - сотни метров, высота антенны МС – несколько метров. На практике дальность радиогоризонта равна примерно 25 км и 50 км при высоте антенны БС соответственно 50 м и 200 м.

Экспериментально установлено (рис.3), что влияние высоты антенны МС не зависит от протяженности трассы, поскольку эти антенны расположены ниже уровня городской застройки. На рис. 3 кривая 1 соответствует крупному городу, кривая 2- среднему городу при f=400 МГц и кривая 3 – среднему городу при f=2 ГГц. Кроме того, при hАС <3 м влияние антенны МС одинаково на всех частотах и не зависит от характера застройки.
Экспериментальные данные позволяют записать
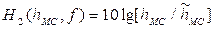 (1.3)
(1.3)
При установке антенны МС выше трех метров значение коэффициента 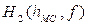 становится зависимым от характера застройки. Для среднего города этот коэффициент зависит от частоты. При
становится зависимым от характера застройки. Для среднего города этот коэффициент зависит от частоты. При 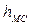 >3 м для среднего города имеем:
>3 м для среднего города имеем:
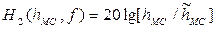 при f=400 МГц
при f=400 МГц
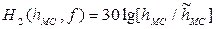 при f=2000 МГц.
при f=2000 МГц.
Для крупных городов коэффициент «высота-усиление антенны МС» не зависит от частоты и при 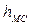 >3 м остается справедливым соотношение (1.3).
>3 м остается справедливым соотношение (1.3).
Модель Окамуры позволяет для местности, которая не относится к квазигладкой, введением поправочных коэффициентов в (1.1)рассчитывать ожидаемый уровень медианой мощности сигнала с учетом характера местности:
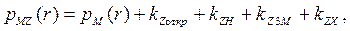 (1.4)
(1.4)
где 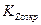 - поправочный коэффициент для пригородной зоны и открытой местности;
- поправочный коэффициент для пригородной зоны и открытой местности;  - поправочный коэффициент для трассы с наклоном;
- поправочный коэффициент для трассы с наклоном; 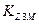 - поправочный коэффициент для участка «земля-море»;
- поправочный коэффициент для участка «земля-море»; 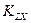 - поправочный коэффициент для холмистой местности.
- поправочный коэффициент для холмистой местности.
В пригородной зоне потери сигнала при распространении меньше, чем в городе, поскольку в ней ниже здания и меньше препятствий. Как установил Окамура, эти потери уменьшаются с ростом частоты, то есть коэффициент 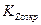 растет. Его значения можно определить по табл.2.
растет. Его значения можно определить по табл.2.
Табл.2.
| f, МГц | 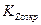 , дБ , дБ
| |
| Пригород | Открытая местность | |
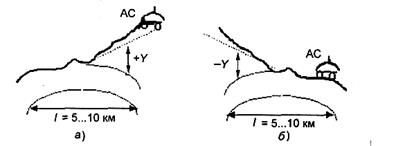
Под трассами с наклоном подразумевают трассы, на которых рельеф плавно понижается (или повышается) на расстоянии 5 км и более. Для нее определяют средний угол наклона 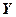 (рис.4,а). Угол считается отрицательным, если МС расположена на нижнем участке трассы (рис.4, б).
(рис.4,а). Угол считается отрицательным, если МС расположена на нижнем участке трассы (рис.4, б).
|
|
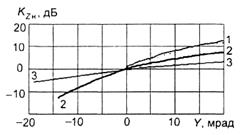
 (рис.5.).
(рис.5.).
|
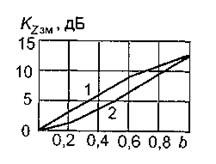
Мощность сигнала возрастает, если трасса пересекает водную поверхность. Коэффициент 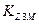 зависит от отношения b=rв/r, где rв – протяженность трассы над водой. Кривая 1 на рис.6 определяет
зависит от отношения b=rв/r, где rв – протяженность трассы над водой. Кривая 1 на рис.6 определяет 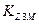 для случая, когда водная поверхность ближе к приемной станции, кривая 2 – к передающей.
для случая, когда водная поверхность ближе к приемной станции, кривая 2 – к передающей.
 | |||
| |||
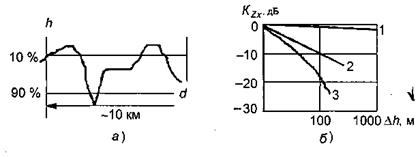
При распространении сигнала над холмистой поверхностью потери распространения увеличиваются по сравнению со случаем квазигладкой местности. Значение  (рис.7,б) зависит от
(рис.7,б) зависит от 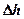 - средней высоты неровностей, которая может быть определена по рис.7,а как разность между высотами h (90%) и h (10%). Здесь h (90%) и h (10%) – значения высот местности на трассе протяженностью около 10 км, превышаемые в 90% и 10% точек профиля соответственно. Значения
- средней высоты неровностей, которая может быть определена по рис.7,а как разность между высотами h (90%) и h (10%). Здесь h (90%) и h (10%) – значения высот местности на трассе протяженностью около 10 км, превышаемые в 90% и 10% точек профиля соответственно. Значения 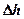 определяют по табл.3., причем условие квазигладкой местности нарушается при
определяют по табл.3., причем условие квазигладкой местности нарушается при 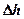 >20м.
>20м.
Табл.3.
| Тип местности | 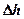 , м , м
| Тип местности | 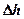 , м , м
|
| Слегка холмистая равнина | 20…40 | Горы | 150…300 |
| Холмистая равнина | 40…80 | Высокие горные массивы | 300…700 |
| Холмы | 80…150 | Очень высокие горные массивы | Свыше 700 |
| |||
 |
Зависимость от длины трассы.В общем случае при удалении МС от БС мощность сигнала, принятого на МС уменьшается по закону
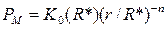 ,(1.5)
,(1.5)
где 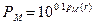 ;
;
n – показатель затухания; R* = 1 км – эталонная длина трассы; 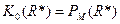 .
.
На основании обработки экспериментальных результатов предложено следующее аналитическое представление для мощности принимаемого сигнала:
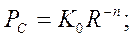 (1.6)
(1.6)
где К0 - медианная мощность сигнала на расстоянии одного километра от БС которую можно рассчитать по (1.2), R - расстояние между БС и МС выраженное в километрах, n – показатель затухания. Для свободного пространства n = 2. В городских условиях показатель n зависит от расстояния и высоты антенны БС как показано на рис.8.
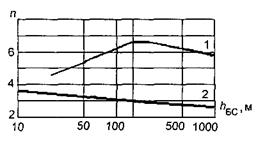
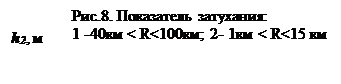
Если расстояние между БС и МС не превышает 15 км, то n = 4 при малой высоте антенны БС, а при больших высотах – n ~ 2.5, т.е. близко к значению в свободном пространстве. Если же R > 40 км, то сигнал резко затухает с увеличением расстояния. В большинстве задач принимают n = 4 в условиях городской застройки. По (1.6) медианная мощность сигнала
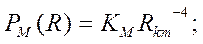 (1.7)
(1.7)
где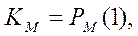 - медианная мощность сигнала на расстоянии 1 км от БС;
- медианная мощность сигнала на расстоянии 1 км от БС;  в км.
в км.
Влияние рабочей частоты. Представим
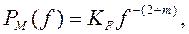 (1.8.)
(1.8.)
где 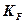 - коэффициент пропорциональности, значение которого можно определить при энергетическом расчете аналогично
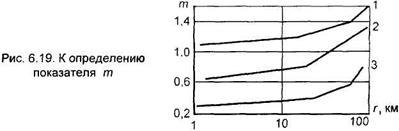
- коэффициент пропорциональности, значение которого можно определить при энергетическом расчете аналогично 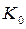 ;m- показатель, установленный экспериментальным путем; f – рабочая частота
;m- показатель, установленный экспериментальным путем; f – рабочая частота
|
|
1.2. Модель Хата.
Результаты экспериментальных измерений Окамуры положены в основу модели Хата. Эмпирические зависимости, используемые в модели Окамуры в виде графиков, в этой модели представлены в виде аппроксимирующих их формул. Согласно этой модели вместо (1.2) представим уровень УММС как
 (1.9)
(1.9)
где 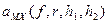 - суммарное ослабление радиосигнала при распространении для модели Хата при статистическом учете параметров местности (а -выражено в децибелах, R– в километрах):
- суммарное ослабление радиосигнала при распространении для модели Хата при статистическом учете параметров местности (а -выражено в децибелах, R– в километрах):
· для города
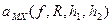 =А+Вlg
=А+Вlg 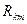 ; (1.10)
; (1.10)
· для пригородной зоны
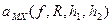 =А+Вlg
=А+Вlg 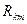 -С; (1.11)
-С; (1.11)
· для открытой местности
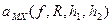 =А+Вlg
=А+Вlg 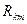 -D;(1.12)
-D;(1.12)
Здесь аппроксимирующие коэффициенты:
А=A(f,h1,h2)=69,55+26,16lg(f)-13,82lg(h1)-a(h2);
В=B(h1)=[44,9-6,55lg(h1)]
С=С(f)=2[lg(f/28)2]+5,4;
D=D(f)=4,78(lgf)2-19,33lg(f)+40,94;
a(h2) – параметр, учитывающий влияние высоты антенны МС.
Для крупных городов этот параметр слабо зависит от частоты, для средних и малых городов этот параметр зависит от частоты, однако используются две аппроксимирующие формулы:
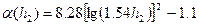 при f ≥ 200 МГц;
при f ≥ 200 МГц;
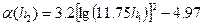 при f ≥ 400 МГц;
при f ≥ 400 МГц;
для средних и малых городов этот параметр зависит от частоты;
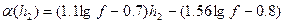
В формулах для аппроксимирующих коэффициентов принято: f – частота излучения БС в МГц; 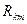 - расстояние между БС и МС в км;
- расстояние между БС и МС в км; 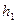 и
и 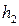 - высоты установки антенны БС и МС. Модель Хата применяют при изменении параметров в пределах, указанных в табл.4.
- высоты установки антенны БС и МС. Модель Хата применяют при изменении параметров в пределах, указанных в табл.4.
Табл.4.
| параметр | частота | высота антенны БС | высота антенны МС | протяженность трассы |
| обозначение | f, МГц | h1, м | h2 , м | R |
| основная область | от 150 до 1500 | от 30 до 200 | от 1 до 10 | от 1 до 20 км |
| расширенная область | от 1.5 до 400 | от 2 до 80 км |
Область применения модели Хата меньше области использования модели Окамуры. Аппроксимирующие выражения по модели Хата совпадают с результатами Окамуры с точностью до 1 дБ в пределах основной области и с меньшей точностью в пределах расширенной области.
Для предсказания уровня сигнала на трассах короче 1 км существуют другие модели.
1.3. Модели Ли
В моделях Ли местность классифицируют по двум признакам:
· по инфраструктуре, сформированной человеком (характер застройки): открытая территория, пригородная зона, городская застройка;
· по естественным свойствам (характер трассы): гладкая, холмистая, трасса над водной поверхностью, трасса через лиственные леса.
Модель «от зоны к зоне» создана на основании анализа результатов измерений уровня сигнала (локального среднего), опубликованных разными авторами для зон с различным характером застройки. В ее основе два следующих экспериментальных параметра модели:
р1 - уровень сигнала в точке, отстоящей от БС на 1 милю (или 1 км);
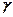 - наклон кривой потерь распространения. Численно равен ослаблению сигнала при увеличении длины трассы в 10 раз; единица измерения – дБ на декаду (дБ/дек).
- наклон кривой потерь распространения. Численно равен ослаблению сигнала при увеличении длины трассы в 10 раз; единица измерения – дБ на декаду (дБ/дек).
Согласно этой модели, уровень мощности на входе приемника МС
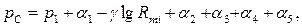 (1.13)
(1.13)
где 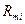 - протяженность трассы, выраженная в милях (миля = 1,6 км);
- протяженность трассы, выраженная в милях (миля = 1,6 км); 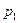 и
и 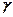 - параметры модели, определенные при типовых энергетических параметрах аппаратуры указанных в табл.5.
- параметры модели, определенные при типовых энергетических параметрах аппаратуры указанных в табл.5. 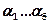 – поправочные коэффициенты; вводятся в случае, когда технические параметры отличаются от типовых параметров модели (табл.5).
– поправочные коэффициенты; вводятся в случае, когда технические параметры отличаются от типовых параметров модели (табл.5).
Табл.5.
| Параметры | стандартные значения | поправочные коэфициенты |
| Уровень мощности передатчика БС - рБС | рБС * = 40 дБм | 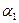 = рБС – 40 = рБС – 40
|
| Высота антенны БС – h1 | h1* = 100 фут (30м) | 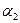 = 20lg(h1/h1*) = 20lg(h1/h1*)
|
| Коэффициент усиления антенны БС – g1 | g1* = 6 дБ | 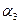 = g1 – 6 = g1 – 6
|
| Высота антенны МС – h2 | h2*=10фут (3м) | 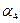 =10lg(h2/h2*) =10lg(h2/h2*)
|
| Коэффициент усиления антенны МС – g2 | g2*=0 дБ | 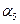 = g2 = g2
|
|
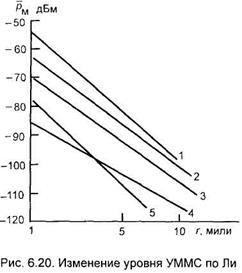
Для определения параметров модели использованы результаты измерений мощности сигнала на трассах. Зависимости уровня мощности сигнала, измеренные для этих трасс показаны на рис.10.
|
 Эти результаты получены при определенных стандартных параметрах, указанных в табл.6.
Эти результаты получены при определенных стандартных параметрах, указанных в табл.6.
Табл.6.
| № | трасса | р1, дБм | 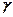 , дБ/дек , дБ/дек
| № | трасса | р1, дБм | 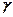 , дБ/дек , дБ/дек
|
| открытая | -49 | 43,5 | Токио | -84 | 30,5 | ||
| типовая пригородная | -61,7 | 38,4 | Нью Йорк Сити | -77 | |||
| Филадельфия | -70 | 36,8 | свободное пространство | -45 |
Подставив в (1.13) параметры модели Ли для трассы «типовая пригородная» и выражение для 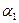 из табл.5. записывают уровень мощности сигнала на входе приемника МС:
из табл.5. записывают уровень мощности сигнала на входе приемника МС:
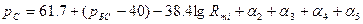 , дБм, (1.14)
, дБм, (1.14)
Поправка при протяженности трассы (R) в километрах (1 миля = 1.6 км).:Z1=38.4lg(R/1.6)=38.4lgR-7.84.
При стандартных параметрах (см. табл.5.) уровень мощности сигнала на расстоянии 1 км от БС (в дБм) 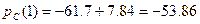 . Подставив величины
. Подставив величины 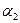 и
и 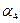 в (1.14) находим
в (1.14) находим 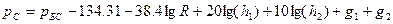 .
.
Окончательно в модели Ли для трассы «типовая пригородная» принят наклон 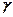 = 40 дБ/дек (40 дБ на декаду) и указана контрольная точка R = 10 миль, в которой уровень мощности сигнала равен -100дБм. Расчетная формула для модели Ли
= 40 дБ/дек (40 дБ на декаду) и указана контрольная точка R = 10 миль, в которой уровень мощности сигнала равен -100дБм. Расчетная формула для модели Ли
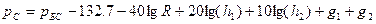 , дБм, (1.15)
, дБм, (1.15)
где R выражено в км, а h1 и h2 - в м.
Физический смысл слагаемых в (1.15) поясняется в табл.7.
Табл.7.
| Слагаемое формулы | Физический смысл |
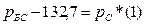
| уровень мощности сигнала на расстоянии 1 км от БС при стандартных условиях, дБм |
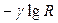
| учитывает влияние сформированной структуры
( 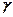 = 40 дБ/декада для трассы «типовая пригородная») = 40 дБ/декада для трассы «типовая пригородная»)
|
+ 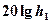
| фактор «высота — усиление антенны БС», учитывающий влияние профиля трассы |
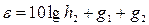
| фактор, учитывающий отклонение технических параметров от стандартных указанных в табл.3. |
Зависимость от длины трассы.Представляют (1.15) в виде
 (1.16)
(1.16)
где 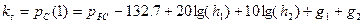 , дБм (1.17)
, дБм (1.17)
- уровень мощности сигнала в точке приема на расстоянии 1 км от БС для трассы «типовая пригородная». Соответствующая мощность сигнала
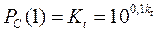 ; мВт. (1.18)
; мВт. (1.18)
Мощность сигнала в точке приема на расстоянии R км от БС, с застройкой типа «типовая пригородная»
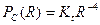 , мВт (1.19)
, мВт (1.19)
Аналогично (1.19) можно записать мощность сигнала в точке приема на расстоянии R км от БС, с застройкой любого типа:
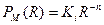 (1.20)
(1.20)
где 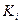 - мощность сигнала в точке приема на расстоянии 1 км от БС, для трассы с заданным типом застройки;
- мощность сигнала в точке приема на расстоянии 1 км от БС, для трассы с заданным типом застройки; 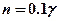 - показатель затухания, зависящий от типа застройки. Значение Ki и n можно найти на основании данных табл.6., а также (1.16).
- показатель затухания, зависящий от типа застройки. Значение Ki и n можно найти на основании данных табл.6., а также (1.16).
При расчете реальных трасс следует сравнить рассматриваемую территорию с подходящей структурой из табл.6. Поскольку все пригородные зоны похожи, то для них используют (1.19). Для городов показатели затухания существенно отличаются. Так, например, для Токио n=3, а для центральной части Нью-Йорка n=5. В модели Ли указано, что в случае необходимости для конкретных трасс могут быть проведены достаточно простые измерения уровня сигнала на расстоянии 1 миля и 10 миль от БС. В каждой точке должно быть выполнено по 5 - 7 измерений и их результаты усреднены. Локальные средние значения могут быть подставлены в (1.20).
Сопоставив (1.19) и 1.7), а также (1.20) и (1.6) отмечаем их совпадение.
Дополнительные факторы, которые могут влиять на значение уровня сигнала – это ориентация улиц и близость лесных массивов. При радиальном расположении городских улиц относительно БС возможно возникновение волноводного эффекта, и как следствие, усиление принимаемого сигнала. Принятого на МС сигналы, направления распространения которых параллельны направлениям улиц, имеют уровень мощности на 10…20дБ выше, чем сигналы, приходящие с других направлений. На частотах ниже 1 ГГц этот эффект значительно ославлен. Если траектория радиосигнала пересекает лиственный лес, то нужно учитывать дополнительные потери из за рассеяния его листвой. Эти потери могут добавляться в каждом конкретном случае. Установлено, что чем ближе БС лесного массива тем сильнее ослабление сигнала листвой. Поэтому следует избегать расположения БС вблизи лиственных массивов. Антенны БС должны быть подвешены выше верхушек деревьев.
1.4. Модель Ли «от точки к точке»
Эта модель «от точки к точке» позволяет предсказать уровень сигнала с учетом профиля трассы (рельефа и параметров застройки). При этом предлагается разделять трассы по профилю рельефа местности на открытые и закрытые, подобно тому как это делают для трасс РРЛ. Только в отличие от РРЛ,на мобильной радиолинии на открытой трассе, как правило, нет прямой видимости между антеннамиБСи МС, поскольку линию прямой видимости перекрывают городские строения.
В общем виде вместо (1.15) можно записать
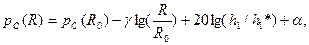 (1.21)
(1.21)
где 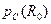 - уровень мощности сигнала на расстоянии
- уровень мощности сигнала на расстоянии 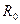 от БС при типовых энергетических параметрах аппаратуры указанных в табл.6.;
от БС при типовых энергетических параметрах аппаратуры указанных в табл.6.;  - результирующий поправочный коэффициент. В (1.21) фактор «высота – усиление антенны БС», позволяет рассчитать изменение коэффициента усиления антенны БС при изменении профиля трассы
- результирующий поправочный коэффициент. В (1.21) фактор «высота – усиление антенны БС», позволяет рассчитать изменение коэффициента усиления антенны БС при изменении профиля трассы
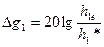 , (1.22)
, (1.22)
где 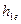 - эффективная высота антенны БС для конкретного участка трассы.
- эффективная высота антенны БС для конкретного участка трассы.
Напомним, что в моделях «от зоны к зоне» эффективная высота антенны БС определяется как высота над средним уровнем квазигладкой поверхности. Для модели «от точки к точке» эффективная высота антенны БС зависит от рельефа трасы и может изменяться при движении МС.
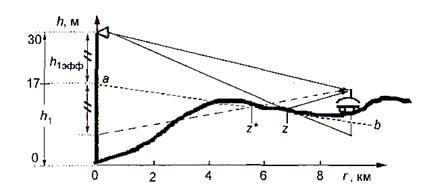
Открытые трассы. Для определения эффективной высоты антенны на профиле трассы выполняют следующие построения (рис. 11). Определяют потенциальную точку z отражения радиоволн от земной поверхности, для чего соединяют антенну БС с зеркальным изображением антенны МС. Точка пересечения этой линии с земной поверхностью и есть z.
|
Строят плоскость отражения от Земли, как касательную к профилю трассы в точке z. Продолжают ее до пересечения с высотой антенны БС. След этой плоскости - линия  . Из рис.11. находим эффективную высоту антенны БС -
. Из рис.11. находим эффективную высоту антенны БС - 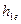 . Для данного примера по (1.22)
. Для данного примера по (1.22)
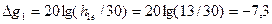 дБ.
дБ.
Эффективная высота антенны меньше реальной, и соответственно уменьшился уровень сигнала в точке приема.
Так же можно определить вторую потенциальную точку отражения на этой плоскости z*, соединив антенну МС с зеркальным изображением антенны БС ( 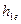 ). Из двух потенциальных точек отражения рекомендуется рассматривать ту, которая ближе к МС, поскольку значительная часть отраженной от нее энергии может попасть к МС. При нахождении точки z следует помнить, что при построении профиля трассы используют разные горизонтальный (Г) и вертикальный (В) масштабы. Например, если для высот в 1 см-100м (1:10 000), а для расстояний - 1:100 000 – 1 км в 1 см, то коэффициент отношения масштабов Г/В составляет
). Из двух потенциальных точек отражения рекомендуется рассматривать ту, которая ближе к МС, поскольку значительная часть отраженной от нее энергии может попасть к МС. При нахождении точки z следует помнить, что при построении профиля трассы используют разные горизонтальный (Г) и вертикальный (В) масштабы. Например, если для высот в 1 см-100м (1:10 000), а для расстояний - 1:100 000 – 1 км в 1 см, то коэффициент отношения масштабов Г/В составляет 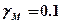 . Углы падения и отражения на чертеже профиля в системе координат с различными масштабами равны только в случае, когда плоскость отражения горизонтальна. В других случаях нет. Приведенный выше метод определения точки отражения применим при
. Углы падения и отражения на чертеже профиля в системе координат с различными масштабами равны только в случае, когда плоскость отражения горизонтальна. В других случаях нет. Приведенный выше метод определения точки отражения применим при  . При
. При 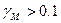 применяют более точные методы.
применяют более точные методы.
На рис.12. эффективная высота антенны увеличилась. В этом случае
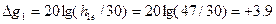 дБ.
дБ.
|
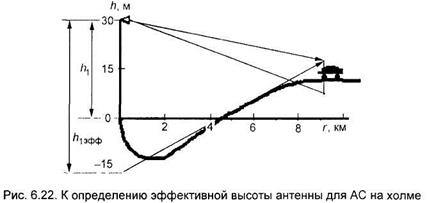
Эффективная высота антенны БС будет меняться при движении МС, хотя реальная высота остается постоянной. Соответственно будет меняться уровень сигнала в точке приема.
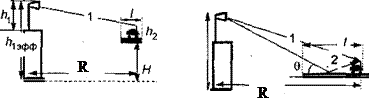
Необходимость учитывать эффективную высоту антенны  вместо реальной иллюстрирует рис. 13. На рис.13,а высота Н >> h2 и длина подстилающей поверхности
вместо реальной иллюстрирует рис. 13. На рис.13,а высота Н >> h2 и длина подстилающей поверхности 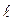 соизмерима с длиной автомобиля. В этом случае на приемник МС приходит только одна прямая волна 1 и условия распространения такие же, как в свободном пространстве. Ситуация на рис.13,б отличается только тем, что значительно увеличилась длина
соизмерима с длиной автомобиля. В этом случае на приемник МС приходит только одна прямая волна 1 и условия распространения такие же, как в свободном пространстве. Ситуация на рис.13,б отличается только тем, что значительно увеличилась длина 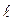 , так что может быть указана потенциальная точка отражения от подстилающей поверхности. На приемник МС приходят два сигнала: прямой 1 и отраженный 2. Поскольку расстояние R обычно составляет несколько километров, а высоты антенн порядка 3...30 м, то угол скольжения
, так что может быть указана потенциальная точка отражения от подстилающей поверхности. На приемник МС приходят два сигнала: прямой 1 и отраженный 2. Поскольку расстояние R обычно составляет несколько километров, а высоты антенн порядка 3...30 м, то угол скольжения 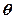 очень мал. При этом фаза коэффициента отражения около 180°. В случае, когда имеет место зеркальное отражение, могут возникать глубокие замирания сигнала на приеме.
очень мал. При этом фаза коэффициента отражения около 180°. В случае, когда имеет место зеркальное отражение, могут возникать глубокие замирания сигнала на приеме.
 |
а) б)
Рис.13. К учету эффективной высоты антенны при малых (а) и больших (б) размерах подстилающей поверхности
На местности с большим уклоном сигнал, приходящий на МС, будет слабым, поскольку рельеф местности ослабляет прямую волну. Эффективная высота антенны становится очень малой.
Отражения от водной поверхности носит зеркальный характер. Для систем с фиксированными станциями, например РРЛ, при расчете трасс над водной поверхностью используется двухлучевая модель (рис.14,а), а при расчете подобных трасс для систем подвижной связи - трехлучевая модель Ли (рис.14,б). При этом предполагается, что волны 2 и 3 складываются в противофазе и компенсируют друг друга. Уровень сигнала такой же как в свободном пространстве.
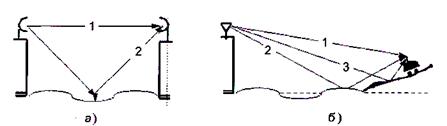
Рис.14. Модели для учета влияния водной поверхности: двухлучевая (а) и трехлучевая (б)
Влияние городской инфраструктуры. На уровень сигнала влияет плотность застройки. При плотной застройке уровень сигнала на приеме ниже, чем при редкой.
При плотной застройке различают варианты:
· Прямая видимость между антеннами БСи МС. Уровень радиоволн, отраженных зданиями мал, в сравнении с основным сигналом. Замирания сигнала подчиняются закону Райса.
· Линия прямой видимости перекрыта строениями. Замирания сигнала подчиняются закону Релея.
В этих двух случаях средняя мощность принимаемого сигнала не одинакова. Однако различия малы, если мощность отраженных волн значительна. В обоих случаях потери распространения составляют примерно 40 дБ на декаду.
Закрытые трассы. На них линия прямой видимости перекрыта профилем местности из-за чего имеют место дифракционные потери. Их рассчитывают, применяя теорию дифракции радиоволн на препятствии клиновидной формы. Выполняют построения, показанные на рис.15.
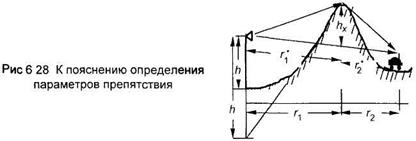
|
|
По профилю трассы определяют три параметра: 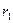 - расстояние от БС до вершины холма;
- расстояние от БС до вершины холма; 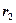 - расстояние от вершины холма до МС;
- расстояние от вершины холма до МС; 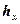 - высоту холма с клиновидной вершиной. И вычисляют параметр
- высоту холма с клиновидной вершиной. И вычисляют параметр 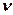 :
:
 (1.23)
(1.23)
где 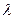 - длина волны.
- длина волны.
Высота препятствия в расчете может принимать отрицательное значение ( 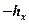 ). Это означает, что трасса открытая и нет дифракционных потерь.
). Это означает, что трасса открытая и нет дифракционных потерь.
Дифракционные потери  выражаются в децибелах. Известно аналитическое представление величины
выражаются в децибелах. Известно аналитическое представление величины  через интегралы Френеля. В инженерной практике пользуются графическим представлением
через интегралы Френеля. В инженерной практике пользуются графическим представлением 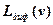 , а также выражениями, аппроксимирующими эти графики.
, а также выражениями, аппроксимирующими эти графики.
Ha касательной трассе если 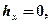 то
то 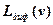 = 6 дБ.
= 6 дБ.
Двойная дифракция. Это случай, когда на трассе имеется несколько холмов. Здесь может возникнуть двойная или даже более сложная дифракция. Для расчета значения потерь используются модели Буллингтона, Эпштейна и Питерсона и др. При использовании модели Пиквинарда определяют высоты холмов, например, С - 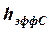 и D -
и D - 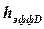 . Находят дифракционные потери отдельно для каждого холма:
. Находят дифракционные потери отдельно для каждого холма:  и
и 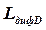 . Общие потери
. Общие потери  .
.
Выводы.
Для модели Ли «от точки к точке» в качестве основной принята формула (1.21), которая может быть распространена на следующие случаи:
1. Открытая трасса. Используют формулу
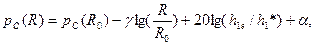 . (1.24)
. (1.24)
2. Закрытая трасса.
 (1.252)
(1.252)
где 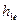 - условная эффективная высота антенны БС на закрытой трассе.
- условная эффективная высота антенны БС на закрытой трассе.
3. Пролет БС - МС над водной поверхностью. Справедлива формула для свободного пространства.
Условную эффективную высоту антенны БС на закрытой трассе часто определить нельзя (не существует). В таком случае принимают 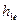 =
= 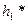 .
.
2. РАСЧЕТ ПОМЕХ
2.1. Чувствительность приемника
Чувствительность приемной установки характеризует ее возможность принимать слабые радиосигналы. Для оценки чувствительности используют минимально допустимое значение напряженности поля радиосигнала в антенне, либо минимальное допустимое значение мощности радиосигнала на входе приемника. Соотношение между этими параметрами установлено при следующих допущениях: приемная антенна МС – диполь; антенна и входная часть приемника согласованы; сопротивление входной цепи приемника 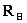 = 50 Ом.
= 50 Ом.
На антенне наводится напряжение
 (2.1)
(2.1)
где Е - напряженность поля радиосигнала, В/м.
При согласовании сопротивлений антенны и входной цепи приемника мощность сигнала на входе приемника
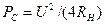 (2.2)
(2.2)
Подставив (2.1) в (2.2), получают
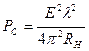 (2.3)
(2.3)
Уровень мощности сигнала на входе приемника, выраженный в децибелах по отношению к 1 мВт,
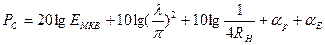 (2.4)
(2.4)
где  - напряженность поля, мкВ/м;
- напряженность поля, мкВ/м; 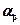 = 30 дБ - коэффициент, учитывающий изменение размерности мощности (переход от Вт к мВт);
= 30 дБ - коэффициент, учитывающий изменение размерности мощности (переход от Вт к мВт);
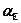 = -120 дБ - коэффициент, учитывающий изменение размерности напряженности поля (переход от В/м к мкВ/м);
= -120 дБ - коэффициент, учитывающий изменение размерности напряженности поля (переход от В/м к мкВ/м);
10lg[1/(4RH)] = 10lg[1/(4∙50)] = -23 дБ.
Подставив указанные численные значения в (2.4), получим, что уровень мощности, дБм, определяется следующими выражениями:
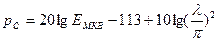 (2.5)
(2.5)
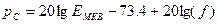 (2.6)
(2.6)
где f- несущая частота, МГц, ЕМКВ – выражено в дБ мкВ/м.
2.2. Тепловые шумы и зона покрытия
На входе приемного устройства МС действуют собственные тепловые шумы (ТШ) и внешние помехи. Внешние помехи подразделяют на индустриальные и шумы излучения. Полагают, что такие внешние помехи в пределах шумовой полосы приемника имеют равномерный спектр, и их оценивают с помощью собственного коэффициента шума.
ТШ приемника. Мощность тепловых шумов приемной установки, пересчитанных ко входу приемника,
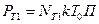 (2.7)
(2.7)
где 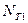 - коэффициент шума приемника;
- коэффициент шума приемника; 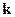 - постоянная Больцмана;
- постоянная Больцмана; 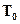 - температура входной цепи, К; П - эффективная ширина шумовой полосы приемника.
- температура входной цепи, К; П - эффективная ширина шумовой полосы приемника.
Уровень мощности теплового шума
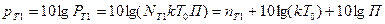 (2.8)
(2.8)
Полагая, что
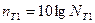 , дБ (2.9)
, дБ (2.9)
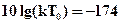 дБм/Гц при
дБм/Гц при 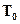 =290 К запишем для уровня мощности теплового шума при указанных численных значений:
=290 К запишем для уровня мощности теплового шума при указанных численных значений:
 (2.10)
(2.10)
где 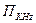 - значение П, выраженное в килогерцах. Типичное значение коэффициента шума приемника
- значение П, выраженное в килогерцах. Типичное значение коэффициента шума приемника 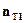 = 7...9 дБ для частот 800...1000 МГц.
= 7...9 дБ для частот 800...1000 МГц.
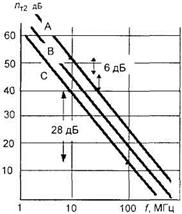
Индустриальные шумы. Это внешние помехи от систем зажигания автомобилей, промышленного оборудования, шумовые излучения высоковольтных линий и др. В рассматриваемых диапазонах частот преобладают шумы от систем зажигания автомобилей. Для шумов индустриального происхождения коэффициент шума 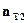 может быть найден по графикам на рис.16. в зависимости от местности: для деловой части города (с высокой плотностью застройки) и высокими зданиями – график А; для жилой части (с меньшей плотностью застройки и менее высокими зданиями) – В; в сельской местности – С. Всем трем местностям соответствует одинаковый наклон графиков примерно 28 дБ/дек. Расстояние между соседними кривыми составляет 6 дБ.
может быть найден по графикам на рис.16. в зависимости от местности: для деловой части города (с высокой плотностью застройки) и высокими зданиями – график А; для жилой части (с меньшей плотностью застройки и менее высокими зданиями) – В; в сельской местности – С. Всем трем местностям соответствует одинаковый наклон графиков примерно 28 дБ/дек. Расстояние между соседними кривыми составляет 6 дБ.
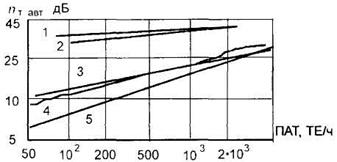
На рис.17. представлена зависимость усредненного значения коэффициента шума, создаваемого системами зажигания (nТА), в зависимости от плотности автомобильного трафика (ПАТ), измеренной числом транспортных единиц в час (ТЕ/ч). Кривые получены для следующих значений несущей частоты; 1) 10 МГц; 2) 20 МГц; 3) 48 МГц; 4) 100 МГц; 5) 700-800 МГц.
|
|
| |||
|
Шумы излучения. Создаются энергией, излучаемой БС и МС. Несмотря на то, что уровень этого излучения жестко ограничен и весьма мал, с этими шумами приходится считаться на тех территориях, где системы подвижной связи широко распространены. Обычно берут nТ3 = 2…3 дБ для БС и nТ3 = 3…4 дБ для МС.
Сложение ТШ. Принимая во внимание, что ТШ от независимых источников суммируются «по мощности», запишем результирующий коэффициент шума;
 ,дБ (2.11)
,дБ (2.11)
В табл.8. приведены nТ, вычисленные с учетом возможных уровней индустриальных шумов для частот 800…1000 МГц.
Табл.8.
| nТ2, дБ | примечание | |||||

| 3,16 | 3,98 | 5,01 | 6,3 | 7,94 | nТ1 = 9 дБ;
 = 7,94 = 7,94
|
| nТ, дБ | 10,45 | 10,76 | 11,12 | 11,53 |
Приняв результирующий коэффициент шума nТ » 11 дБ, можно вычислить по (2.10) уровень мощности NI на входе приемника - 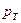 , дБм.
, дБм.
Отношение сигнал-шум на входе приемника
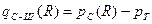 . (2.12)
. (2.12)
На границе зоны покрытия должно выполняться условие
 (2.13)
(2.13)
где 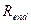 - радиус зоны покрытия;
- радиус зоны покрытия; 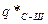 - допустимое значение отношения сигнал-шум, указанное в технических параметрах аппаратуры;
- допустимое значение отношения сигнал-шум, указанное в технических параметрах аппаратуры; 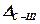 = 5 ...10 дБ - энергетический запас.
= 5 ...10 дБ - энергетический запас.
Значение 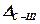 может быть указано в нормативных документах или выбрано оператором системы.
может быть указано в нормативных документах или выбрано оператором системы.
На основании (2.12) и (2.13) запишем минимально допустимый уровень сигнала на границе зоны покрытия:
 (2.14)
(2.14)
Подставив (2.14) в (2.6), вычисляют напряженность поля на границе зоны покрытия
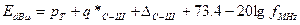 (2.15)
(2.15)
Пример расчета. Для системы стандарта имеем: f = 850 MHz; ПkHz = 30; 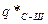 =18дБ. Находим по (2.10)
=18дБ. Находим по (2.10)
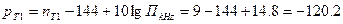 дБм.
дБм.
Приняв результирующий коэффициент шума nТ » 11 дБ, получим уровень мощности ТШ 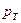 = -118 дБм. Сначала положим
= -118 дБм. Сначала положим 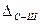 = 0. Минимально допустимый уровень сигнала на границе зоны покрытия
= 0. Минимально допустимый уровень сигнала на границе зоны покрытия  дБм. Формула (2.6) приобретает вид
дБм. Формула (2.6) приобретает вид 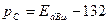 , дБм при f=850 МГц. Следовательно, напряженность поля на границе зоны покрытия
, дБм при f=850 МГц. Следовательно, напряженность поля на границе зоны покрытия 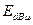 = 32 мкВ/м.
= 32 мкВ/м.
Для разных стран эта величина неодинакова, например, в США установлена граница зоны покрытия по уровню 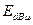 = 39 мкВ/м, что соответствует
= 39 мкВ/м, что соответствует 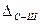 = 7дБ.
= 7дБ.
2.3. Интерференционные помехи на совпадающих частотах
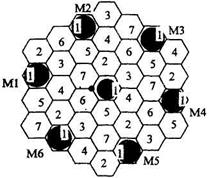
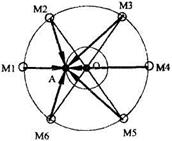
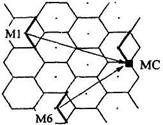
Рассматриваемые помехи попадают на вход приемника МС от БС соседних кластеров. На рис.18. приведен фрагмент частотно – территориального плана (ЧТП), составленного на основе кластера с размерностью N=7. Цифрами 1…7 обозначены частотные группы присвоенные сотам. Рассматриваем воздействие сигнала и интерференционных помех на МС, расположенные в центральной соте. Помехи создают БС, обозначенные М1…М6. Наиболее неблагоприятный случай соответствует минимальному уровню принимаемого сигнала, т.е. положению МС на границы соты (обозначенного жирной точкой). Вместо рис.18. воспользуемся упрощенным рис.19., где местоположение БС - точка О, МС – точка А и местоположение мешающих станций М1…М6. Рассматриваем однородную модель ЧТП при всенаправленных антеннах БС. Для нее известно: а) число МС = 6, при любой размерности кластера; б) расстояние между БС с одинаковой частотой
|
|
|
|
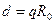 ; (2.16,а)
; (2.16,а) 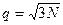 ; (2.16,б)
; (2.16,б) 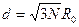 , (2.16,в)
, (2.16,в)
Длины отрезков М1-О…М6-О равны d. Радиус внутренней окружности ОА – радиус соты R0. Расстояние от точки А до МС с номером J обозначим RJ. Их значения вычислим по рис.19. Например, 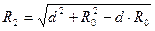 . Используя (2.16,а), получаем расчетную формулу (2.17,б), записанную в табл.9.
. Используя (2.16,а), получаем расчетную формулу (2.17,б), записанную в табл.9.
Табл.9.
| всенаправленная антенна БС | секторная антенна БС, 120о | ||
| мешающая БС | расчетные выражения | мешающая БС | расчетные выражения |
| М1 | 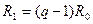 ; (2.17,а) ; (2.17,а)
| М1 | 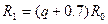 ; (2.18,а) ; (2.18,а)
|
| М2 и М6 |  ; (2.17,б) ; (2.17,б)
| М6 | 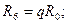 (2.18,б) (2.18,б)
|
| М3 и М5 | 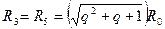 ; (2.18,в) ; (2.18,в)
| ||
| М4 |  ; (2.17,г) ; (2.17,г)
|
Мощности сигналов, приходящих на МС, представим в виде (1.3), приняв 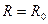 для своего сигнала и
для своего сигнала и 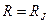 для J-го мешающего сигнала. Если энергетические параметры БС в сети одинаковы, то отношение медианной мощности J-го мешающего к медианной мощности своего сигнала
для J-го мешающего сигнала. Если энергетические параметры БС в сети одинаковы, то отношение медианной мощности J-го мешающего к медианной мощности своего сигнала
 . (2.19)
. (2.19)
При нескольких мешающих сигналах на МС воздействует суммарная помеха, медианная мощность которой равна сумме медианных мощностей отдельных сигналов. Медианное отношение сигнал-интерференция
 , дБ (2.20)
, дБ (2.20)
где m – число мешающих сигналов. Для однородной модели m=6. По (2.20) можно найти усредненное медианное отношение сигнал – интерференция. Замирания сигналов не учтены.
|
Эффективным способом повышения отношения сигнал-интерференция является применение секторных антенн. Фрагменты ЧТП при N=7 с использованием секторных антенн с шириной ДНА a = 120о и a = 60о показаны на рис.20 и 21. Секторы сот, в которых использованы одинаковые частоты, обозначены жирными линиями. При a = 120о осталось два мешающих сигнала и изменилось RJ , как показано в табл.9. Для варианта a = 60о остался только один мешающий сигнал и расстояние 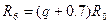 ; совпадает с расстоянием в табл.9.
; совпадает с расстоянием в табл.9.

|
|
2.4. Интерференционные помехи от соседних и ближайших каналов
В системах подвижной связи используются понятия «частотный план» (ЧП) и «частотно-территориальное планирование» (ЧТП). Частотный план присваивается стандарту и определяет распределение частот приема и передачи между каналами. Частотные планы для ряда стандартов были рассмотрены ранее (см. лекцию №2, рис.2-4). Частотные каналы, расположенные в таком плане рядом, называются ближайшими.
ЧТП разрабатывают для конкретной территории, на которой развернута система. В нем указывается размерность кластера; распределение частотных групп между сотами; расположение сот на территории; число каналов в каждой частотной группе, присвоенной соте; номинальные значения частот каналов в такой группе. На БС к одной антенне может б
Дата добавления: 2015-01-13; просмотров: 4430;
