Лекция №3. Любой результат измерений содержит погрешность из-за наличия погрешностей, присущих самому средству измерений

1.ПОГРЕШНОСТЬ РЕЗУЛЬТАТА ИЗМЕРЕНИЙ

Любой результат измерений содержит погрешность из-за наличия погрешностей, присущих самому средству измерений, выбранным методу и методике измерений, из-за влияния внешних условий и других причин, вызывающих погрешности. Погрешность вычисляется или оценивается, или приписывается полученному результату.

Погрешности можно разделить по признакам:

· по способу выражения – абсолютные и относительные;

· по характеру проявления – систематические и случайные;

· по условиям измерения измеряемой величины – погрешность воспроизведения единицы, хранения единицы, передачи размера единицы физической величины.

1.1. Абсолютная и относительная погрешности

Погрешность результата измерения – это отклонение результата измерения от истинного значения измеряемой величины.

Истинное значение величины остается неизвестным в связи с наличием погрешностей. На практике используется действительное значение величины, которое заменяет истинное значение.

Погрешность находят по формуле

Dx_ист = х_изм – Х, (1)

где Dx_ист – погрешность измерения; Dx_ист – значение величины, полученное в результате измерения; Х – истинное значение величины.

Или Dx_д = х_изм – Х_д, (2)

где Х_д – значение величины, принятое за действительное.

Истинное значение величины познается только в результате бесконечно большого числа измерений с бесконечным совершенствованием методов и средств измерений, т. е. Dx_д ®0, при n® ¥, где п — число измерений.

По формуле (1) находят абсолютную погрешность измерения, выражающуюся в единицах измеряемой величины.

Относительная погрешность измерения есть отношение абсолютной погрешности измерения к действительному значению измеряемой величины. Она выражается в долях значения измеряемой величины или в процентах. Относительную погрешность находят по формулам:

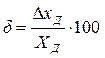
Например, если действительное значение массы Хд=10 кг, а абсолютное значение погрешности Dх==0,01 кг, то относительная погрешность составит

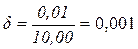или .

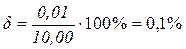Использование относительных погрешностей в ряде случаев значительно удобнее, так как по значению относительной погрешности можно судить о качестве полученного результата.

1.2.СИСТЕМАТИЧЕСКИЕ И СЛУЧАЙНЫЕ ПОГРЕШНОСТИ. ГРУБЫЕ ПОГТЕШНОСТИ

1.2.1.КЛАССИФИКАЦИЯ СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ.

Систематическая погрешность измерения — составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. Эти погрешности могут быть в большинстве случаев изучены до начала измерений, и результат измерения может быть уточнен или путем внесения поправок, если числовые значения этих погрешностей определены, или путем использования таких способов измерений, которые дают возможность исключить влияние систематических погрешностей без их определения. Результаты измерений тем ближе к истинному значению, чем меньше оставшиеся не исключенные систематические погрешности.

По характеру проявления систематические погрешности подразделяются на постоянные, прогрессивные и периодические (рисунок 1).

Постоянные погрешности – погрешности, длительное время сохраняющие свое значение. Они встречаются наиболее часто. К постоянным относятся погрешности большинства мер (гирь, концевых мер длины), погрешности градуировки шкал измерительных приборов и др. Например, погрешность от постороннего груза на чашке весов, погрешность от неточной установки прибора на нуль.

Прогрессивные погрешности – непрерывно возрастающие или убывающие погрешности. К ним относятся погрешности от износа контактирующих деталей средств измерении, постепенное падение напряжения источника тока (аккумуляторных батарей), погрешность от постепенного прогрева измерительной аппаратуры и др.

Периодические погрешности – погрешности, периодически изменяющие значение и знак. Обычно эта погрешность встречается в угломерных приборах с круговой шкалой. Например, погрешность от эксцентриситета круговой шкалы и оси вращения стрелки средства измерений.

Погрешности, изменяющиеся по сложному закону, появляются вследствие действия нескольких систематических погрешностей.

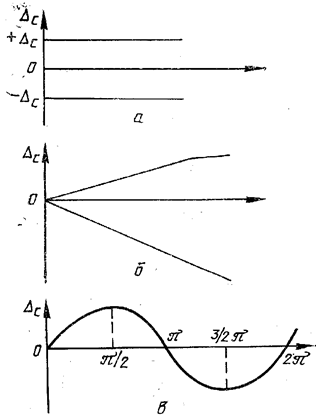
Рисунок 1 – Виды систематических погрешностей:

а) постоянные; б) прогрессивные; в) периодические

При подготовке, проведении, обработки результатов измерений стараются в максимальной степени или исключить, или учесть влияние систематических погрешностей. Условно можно выделить четыре основные группы мероприятий:

· устранение источников погрешностей до начала измерений

· устранение погрешностей в ходе измерений;

· внесение известных поправок в результат измерения;

· оценка границ неисключенных систематических погрешностей.

1.2.2.СЛУЧАЙНАЯ ПОГРЕШНОСТЬ

Случайная погрешность измерения это составляющая погрешности результата измерения, изменяющая­ся случайным образом (по знаку и значению) при повторных изме­рениях, проведенных с одинаковой тщательностью, одной и той же физической величины. Эта погрешность возникает вследствие вариации показаний измерительного прибора, погрешности округления при отсчитывании показаний измерительного прибора, изменений условий измерения случайного характера и т. д. Случайные погрешности не поддаются исключению из результатов измерений, как систематические.

Установлены два положения теории погрешностей:

1 – при большом числе измерений случайные погрешности одинакового числового значения, но разного знака встречаются одинаково часто;

2 – большие по абсолютному значению погрешности встречаются реже, чем малые.

Из этого следует, что при увеличении числа измерений случайная погрешность результата полученного из серии измерений уменьшается, так как погрешности компенсируют друг друга по знаку, и их сума стремится к нулю.

Согласно теории погрешностей проведение повторных измерений дает возможность, используя методы теории вероятности и математической статистики, уточнить результат, т. е. приблизить значение измеряемой величины к истинному ее значению.

Вследствие влияния случайных погрешностей результаты повторных измерений незначительно расходятся между собой. Максимально приближенным к истинному значению будет среднее арифметическое 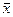значение результатов измерений:

,

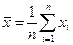где 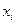– результат наблюдения; п – число единичных наблюдений.

Случайные погрешности вызывают разброс результатов отдельных измерений и оцениваются характеристиками такого разброса (рассеивания) экспериментальных данных. Это рассеивание характеризуется параметрами:

1 – Размах результатов измерений (R): оценка рассеяния результатов единичных измерений физичес­кой величины, образующих ряд (или выборку из n измерений), вычисляемая по формуле: R_n = х_max – х_min, где х_max, х_min – наибольшее и наименьшее значения физичес­кой величины в данном ряду измерений;

2 – Средняя квадратическая погрешность результатов единич­ных измерений в ряду измерений (S): оценка рассеяния единичных результатов измерений в ряду рав­ноточных измерений одной и той же физической величины около среднего их значения. Среднее квадратическое отклонение S ре­зультата единичного наблюдения, взятого из совокупности таких из­мерений, вычисляют по формуле:

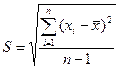. (3)

3 – Средняя квадратическая погрешность результата измерений (среднего арифметического) (S_x): оценка случайной погрешности среднего арифметического зна­чения результата измерений одной и той же величины в данном ряду измерений. Среднее квадратическое отклонение S{x) результата измерения является параметром функции распределения и подсчитывается по формуле:

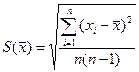, (4)

где 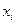– i-й результат наблюдения; 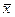– среднее арифметическое исправленных результатов наблюдений (результат измерения); п – число наблюдений.

Из формул (3) и (4) следует, что точность среднего арифметического значения измеряемой величины в 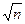раз выше точности единичного наблюдения.

1.2.3.ГРУБЫЕ ПОГРЕШНОСТИ

Грубая погрешность измерения это погрешность измерения, существенно превышающая ожидаемую погрешность при данных условиях. Результаты измерений, содержащие грубые погрешности, в расчет не берутся. Основными причинами этих погрешностей являются ошибки экспериментатора, резкое и неожиданное изменение условий измерения, неисправность прибора и др. Грубые погрешности не всегда легко обнаружить, для выявления грубых ошибок используют статистические методы.

2. Обработка результатов измерений

Для повышения точности измерений, исключения ошибок и из­вестных систематических погрешностей рекомендуется проводить измерения многократными наблюдениями, число которых должно быть не менее трех. Порядок обработки результатов пря­мых многократных измерений и оценки их погрешностей регламен­тирует ГОСТ. При статистической обработке результатов наблюдений выполняют операции:

· исключают известные систематические погрешности из резуль­татов наблюдений;

· вычисляют среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения;

· находят оценку среднего квадратического отклонения резуль­тата измерения;

· устанавливают доверительные границы случайной погрешности результата измерения (при этом проверяют гипотезу о том, что ре­зультаты наблюдений принадлежат нормальному распределению);

· исключают из ряда наблюдений грубые погрешности.