Аккумулирующая емкость магистрального газопровода
Последний участок магистрального газопровода от компрессорной станции до города работает с непрерывно изменяющимся отбором газа. Если подачу газа компрессорной станцией в начало газопровода можно считать примерно постоянной, то отбор газа из конца газопровода зависит от режима потреблении и при отсутствии газохранилищ строго ему соответствует. Таким образом, работа последнего участка магистрального газопровода характеризуется нестационарным режимом (с непрерывно изменяющейся нагрузкой).
В ночное время, когда потребление газа меньше подачи, избыток его накапливается в газопроводе, в результате чего в нем возрастает давление. Количество аккумулированного газа зависит от максимально возможного давления в газопроводе. Если к концу ночного периода в газопроводе будет достигнут максимум давления, т. е. аккумулирующая емкость последнего участка будет исчерпана, а отбор газа из него будет меньше подачи, то придется уменьшить производительность последней компрессорной станции, остановив часть агрегатов. В этом случае накопление газа начнется в предпоследнем участке магистрального газопровода. В дневное время потребление газа превышает подачу, аккумулированный газ поступает из газопровода в город и давление в газопроводе падает.
Решение задачи определения аккумулирующей емкости газопровода основано на замене нестационарного режима движения газа стационарным в моменты, когда отбор газа равен потреблению. В действительности, чтобы режим стабилизировался, необходимо некоторое время, так как при непрерывно изменяющемся потреблении стабильная кривая давления устанавливаться не успевает. Приближенное решение предполагает, что в моменты, когда подача газа равна отбору, режим движения в газопроводе стационарен. Аккумулирующая емкость магистрального газопровода, определенная по приближенной методике, оказывается на 10—15%' меньше действительной.
Чтобы определить, какое количество газа способен аккумулировать газопровод, следует рассчитать массу газа, находящуюся в сети. Ее находят по следующим уравнениям:
dM=Fρdx;
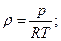
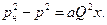
Так как приведенные формулы дают приближенное решение, коэффициент сжимаемости не учитывают.
Дата добавления: 2015-02-25; просмотров: 1455;
