Теория лабораторной работы. Название “метод магнетрона” связано с тем, что применяемая в работе конфигурация электрического и магнитного полей очень напоминает конфигурацию полей в
Название “метод магнетрона” связано с тем, что применяемая в работе конфигурация электрического и магнитного полей очень напоминает конфигурацию полей в магнетронах.
Движение электронов в данной работе происходит в кольцеобразном пространстве между катодом и анодом двух электродной электронной лампы. Нить лампы (катод) располагается вдоль оси цилиндра (анода) так, что электрическое поле направлено по радиусу. Лампа помещается внутри соленоида, создающего магнитное поле, параллельное катоду.
Рассмотрим траекторию электрона под действием комбинации электрического и магнитного полей. Воспользуемся цилиндрической системой координат (рис.8): 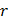 – расстояние от оси цилиндра,
– расстояние от оси цилиндра,  – полярный угол.
– полярный угол.
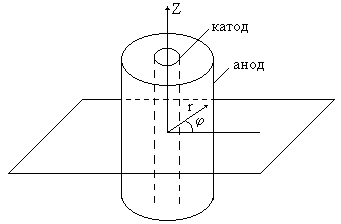 Рис. 8.
Рис. 8.
|
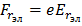 ,
,
где 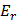 -напряженность электрического поля, направленная по радиусу. Другие компоненты электрических сил в радиальном поле отсутствуют, поэтому
-напряженность электрического поля, направленная по радиусу. Другие компоненты электрических сил в радиальном поле отсутствуют, поэтому
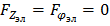 .
.
Рассмотрим силы, действующие на электрон со стороны магнитного поля. Так как магнитное поле направлено вдоль оси Z, то:
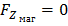 ,
, 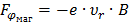 ,
, 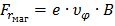 .
.
Соответственно: 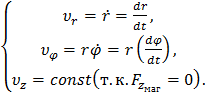
Движение в плоскости 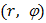 описывается с помощью основного уравнения динамики вращательного движения:
описывается с помощью основного уравнения динамики вращательного движения:
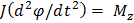 ,
,
где 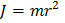 –момент инерции электрона относительно оси
–момент инерции электрона относительно оси 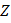 , m–масса электрона,
, m–масса электрона, 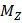 – момент силы вдоль оси
– момент силы вдоль оси 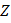 .
.
С другой стороны,
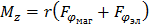 .
.
Подставив значение 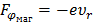 и учитывая, что
и учитывая, что 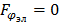 , получим:
, получим:
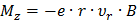 ,
,
где В–индукция магнитного поля, а 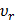 – скорость вдоль радиуса.
– скорость вдоль радиуса.
Окончательно:
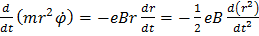 .
.
Интегрируя это уравнение и замечая, что заряд электрона отрицательный, получим:
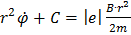 ,
,
где С–постоянная интегрирования.
Учитывая, что электроны вылетают из катода с малой скоростью, можно положить 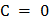 . Тогда уравнение приобретет вид:
. Тогда уравнение приобретет вид:
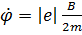 .
.
Рассмотрим теперь движение электрона вдоль радиуса. Работа сил электрического поля 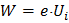 , где
, где 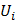 –потенциал точки, в которую переместился электрон. Магнитное поле работы не производит, следовательно,
–потенциал точки, в которую переместился электрон. Магнитное поле работы не производит, следовательно, 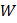 определяет кинетическую энергию электрона:
определяет кинетическую энергию электрона:
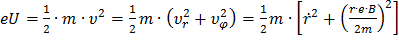 .
.
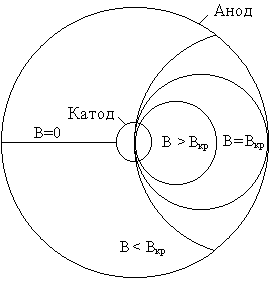 Рис. 9.
Рис. 9.
|
Движение электрона при различных значениях индукции магнитного поля
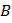 показано на рис. 9.
показано на рис. 9.
Величину 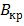 можно найти, заметив, что радиальная скорость
можно найти, заметив, что радиальная скорость 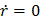 , при
, при 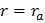 . Отсюда:
. Отсюда: 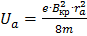 .
.
Для отношения  получим:
получим: 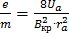 , (1)
, (1)
где  -радиус анода.
-радиус анода.
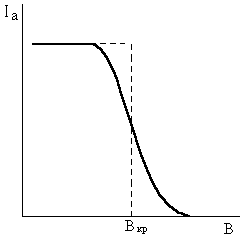 Рис. 10.
Рис. 10.
|
Дата добавления: 2015-02-23; просмотров: 853;
