Краткие теоретические сведения. Испытания на растяжение и характерные точки диаграммы растяжения

Испытания на растяжение и характерные точки диаграммы растяжения. В большинстве случаев металлические материалы в конструкциях работают при статических нагрузках. Поэтому статические испытания широко распространены и проводятся с использованием разных схем напряженного состояния в образце. К основным разновидностям статических испытаний относятся испытания на растяжение, сжатие, изгиб и кручение.

Испытания на одноосное растяжение – наиболее распространенный вид испытаний для оценки механических свойств металлов. Методы испытания на растяжение стандартизированы. Помимо основной рабочей части большинство образцов (рис. 11.1) имеют головки различной конфигурации для крепления в захватах.

Рисунок 11.1 – Схема и общий вид образцов для испытаний на растяжение

Механические свойства при растяжении могут быть разделены на две группы – прочностные и пластические.

Прочностные свойства – это характеристики сопротивления материала образца деформации или разрушению. Большинство стандартных прочностных характеристик рассчитывают по положению определенных точек на диаграмме растяжения в виде условных растягивающих напряжений. На практике механические свойства определяют по первичным кривым растяжения в координатах «нагрузка – абсолютное удлинение», которые автоматически записываются на диаграммной ленте испытательной машины.

Пластические свойства определяются в результате сравнения размеров образцов до деформирования и после разрушения.

Для поликристаллов различных металлов все многообразие кривых растяжения можно свести к трем типам (рис. 11.2).

Рисунок 11.2 – Разновидности первичных диаграмм растяжения:

а) хрупкое разрушение; б) разрушение после равномерной деформации; в) разрушение после образования шейки

В зависимости от типа диаграммы меняется набор характеристик, которые по ней можно рассчитать, а также их физический смысл. На рисунке 11.3 нанесены характерные точки, по ординатам которых рассчитывают прочностные характеристики (σ_i=Р_i/F₀). Как видно, на диаграммах других двух типов могут быть нанесены не все эти точки.

Рисунок 11.3 – Обобщенная диаграмма растяжения

Пределом пропорциональности называется наибольшее напряжение, до которого деформация прямо пропорциональна нагрузке:

,

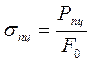где Р_пц – нагрузка, соответствующая линейному участку машинной диаграммы;

F₀ – исходная площадь поперечного сечения образца.

Пределом упругости называется напряжение, при котором остаточное удлинение достигает 0,05 % (иногда 0,005 %) от расчетной длины образца:

,

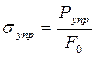где Р_упр – нагрузка, соответствующая точке р, находящейся в непосредственной близости от точки е (рис. 11.3).

Физическим пределом текучести называется напряжение, при котором образец деформируется без заметного увеличения нагрузки:

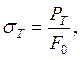
где Р_Т – нагрузка, соответствующая горизонтальному участку диаграммы напряжения.

Условным пределом текучести называется напряжение, при котором остаточное удлинение достигает 0,2 % от длины образца:

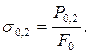
Пределом прочности называется максимальное за время испытания напряжение:

,

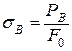где Р_В – максимальная нагрузка.

Условным сопротивлением разрыву называется напряжение в момент разрыва образца:

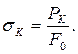
Кроме условного сопротивления разрыву существует истинное сопротивление разрыву, которое определяется отношением нагрузки в момент разрушения к площади поперечного сечения в шейке образца после разрыва :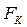

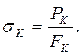
Единицей измерения прочностных свойств в системе СИ является МПа = МН/м², в технической системе единиц – кГс/мм².

Относительным удлинением образца называется отношение приращения расчетной длины образца после разрыва (Δl) к первоначальной расчетной длине (l₀), выраженное в процентах:

.

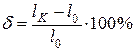Относительным сужением образца называется отношение уменьшения площади поперечного сечения образца к первоначальной площади, выраженное в процентах:

,

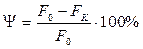где F₀, F_K – площадь поперечного сечения образца до и после разрыва, соответственно.

Поскольку для реальных поликристаллических материалов определение σ_ПЦ и σ_УПР представляет значительные методические трудности из-за очень малых деформаций, соответствующих этим характеристикам, на практике ограничиваются измерением условного и физического пределов текучести, предела прочности и сопротивления разрыву.

Закон Гука и константы упругих свойств. Стадию упругой деформации образцы проходят при всех без исключения видах механических испытаниях.

Поведение металлов при упругой деформации описывается законом Гука, который определяет прямую пропорциональность между напряжением и упругой деформацией. На рисунке 11.4 показаны начальные (упругие) участки кривых «напряжение – деформация» при одноосном растяжении, кручении и гидростатическом сжатии.

Рисунок 11.4 – Упругие участки кривых «напряжение – деформация»:

а – одноосное растяжение; б – кручение; в – гидростатическое сжатие

Тангенс угла наклона каждой из этих трех кривых называется модулем упругости:

E=S/e; G=t/g; K=P/χ.

Модуль E, определяемый при растяжении, называется модулем нормальной упругости или модулем Юнга.

Модуль G – модуль сдвига (касательной упругости).

Модуль К – модуль объемной упругости (Р – гидростатическое давление, χ – уменьшение объема).

Модули упругости определяют жесткость материала, т. е. интенсивность увеличения напряжения по мере упругой деформации.

Механизм упругой деформации металлов состоит в обратимых смещениях атомов из положения равновесия в кристаллической решетке. Чем больше величина смещения каждого атома, тем больше упругая макродеформация всего образца. Величина упругой деформации металлов не может быть большой (относительное удлинение в упругой области обычно меньше одного процента), т. к. атомы кристаллической решетки способны упруго смещаться лишь на небольшую долю межатомного расстояния. Физический смысл модулей упругости состоит в том, что они характеризуют сопротивляемость металлов упругой деформации, т. е. смещению атомов из положений равновесия в решетке. Если сравнивать два металла, например, с разными е (рис. 11.4 а, прямые 1, 2), то для одинакового смещения атомов (равной упругой деформации) при большем е потребуется большее напряжение (прямая 2). При сложных схемах напряженного состояния деформация может не совпадать по направлению с напряжением. Для изотропного тела закон Гука, устанавливающий линейную связь между напряжениями и деформациями в любых направлениях, выражается формулами:

e_x = 1/E·[S_x-ν·(S_y+S_z)],

e_y = 1/E·[S_y-ν·(S_x+S_z)],

e_z = 1/E·[S_z-ν·(S_x+S_y)],

g_xy = t_xy/G,

g_xz = t_xz/G,

g_yz = t_yz/G,

где ν – коэффициент Пуассона при одноосном растяжении (сжатии), характеризующий отношение поперечной относительной деформации к продольной.

Коэффициент Пуассона ν – четвертая важнейшая константа упругих свойств после модулей упругости. Эти четыре константы связаны между собой:

E = 2·G·(1+ν);

E = 3·K·(1-2·ν).

Зная две из них, можно рассчитать остальные.

Обобщенный закон Гука записывается относительно просто для изотропного тела, каким является, например, поликристалл. Монокристаллы являются телами анизотропными. Чем меньше расстояние между соседними атомами, тем больше в данном направлении должен быть модуль упругости. Для анизотропного тела закон Гука существенно усложняется: он отражает прямую пропорциональность между каждым компонентом тензора деформации и всеми шестью независимыми компонентами тензора напряжений.

Модули упругости являются важнейшими характеристиками жесткости межатомной связи. Их величина зависит от всех факторов, определяющих силы межатомного взаимодействия. С повышением температуры модули упругости снижаются. При легировании металлов элементами, образующими твердые растворы, модули упругости меняются линейно, причем могут увеличиваться или уменьшаться.